Ableh-ye Sofla, Ableh-ye Sofla, Manfred Abelein

Ableh-ye Sofla: Ableh-ye Sofla ແມ່ນ ໝູ່ ບ້ານ ໜຶ່ງ ໃນເມືອງຊົນນະບົດ Holayjan, ໃນເຂດພາກກາງຂອງເມືອງ Izeh, ແຂວງ Khuzestan, ອີຣ່ານ. ໃນການ ສຳ ຫຼວດພົນລະເມືອງປີ 2006, ພົນລະເມືອງຂອງຕົນແມ່ນ 215 ຄົນ, ໃນ 38 ຄອບຄົວ.
Ableh-ye Sofla: Ableh-ye Sofla ແມ່ນ ໝູ່ ບ້ານ ໜຶ່ງ ໃນເມືອງຊົນນະບົດ Holayjan, ໃນເຂດພາກກາງຂອງເມືອງ Izeh, ແຂວງ Khuzestan, ອີຣ່ານ. ໃນການ ສຳ ຫຼວດພົນລະເມືອງປີ 2006, ພົນລະເມືອງຂອງຕົນແມ່ນ 215 ຄົນ, ໃນ 38 ຄອບຄົວ.
Manfred Abelein: Manfred Abelein ແມ່ນນັກການເມືອງເຢຍລະມັນ. ລາວເປັນຕົວແທນຂອງສະຫະພັນສາທາລະນະປະຊາທິປະໄຕເຢຍລະມັນ.
Abelemkpe: ເມືອງ Abelenkpe ແມ່ນເຂດຕົວເມືອງໃນເມືອງ Accra Metropolitan, ເຊິ່ງເປັນເມືອງ ໜຶ່ງ ຂອງເຂດ Greater Accra ໃນປະເທດການາ.
ພາສາ Abellen: Abellen , Abenlen , Aburlin, ຫຼື Ayta Abellen ແມ່ນພາສາ Sambalic. ມັນມີຜູ້ເວົ້າປະມານ 3500 ຄົນແລະເວົ້າໃນຊຸມຊົນ Aeta ໃນແຂວງ Tarlac, ປະເທດຟີລິບປິນ Ayta Abellen ເອງແມ່ນສ່ວນ ໜຶ່ງ ຂອງຄອບຄົວພາສາ Sambalic ໃນປະເທດຟີລິບປິນແລະມີຄວາມກ່ຽວຂ້ອງຢ່າງໃກ້ຊິດບໍ່ພຽງແຕ່ 5 ພາສາອື່ນໆຂອງ Ayta, ແຕ່ຍັງມີພາສາເວົ້າຂອງ Botolan ຂອງ ສົມບັດ.
ພາສາ Abellen: Abellen , Abenlen , Aburlin, ຫຼື Ayta Abellen ແມ່ນພາສາ Sambalic. ມັນມີຜູ້ເວົ້າປະມານ 3500 ຄົນແລະເວົ້າໃນຊຸມຊົນ Aeta ໃນແຂວງ Tarlac, ປະເທດຟີລິບປິນ Ayta Abellen ເອງແມ່ນສ່ວນ ໜຶ່ງ ຂອງຄອບຄົວພາສາ Sambalic ໃນປະເທດຟີລິບປິນແລະມີຄວາມກ່ຽວຂ້ອງຢ່າງໃກ້ຊິດບໍ່ພຽງແຕ່ 5 ພາສາອື່ນໆຂອງ Ayta, ແຕ່ຍັງມີພາສາເວົ້າຂອງ Botolan ຂອງ ສົມບັດ.
ພາສາ Abellen: Abellen , Abenlen , Aburlin, ຫຼື Ayta Abellen ແມ່ນພາສາ Sambalic. ມັນມີຜູ້ເວົ້າປະມານ 3500 ຄົນແລະເວົ້າໃນຊຸມຊົນ Aeta ໃນແຂວງ Tarlac, ປະເທດຟີລິບປິນ Ayta Abellen ເອງແມ່ນສ່ວນ ໜຶ່ງ ຂອງຄອບຄົວພາສາ Sambalic ໃນປະເທດຟີລິບປິນແລະມີຄວາມກ່ຽວຂ້ອງຢ່າງໃກ້ຊິດບໍ່ພຽງແຕ່ 5 ພາສາອື່ນໆຂອງ Ayta, ແຕ່ຍັງມີພາສາເວົ້າຂອງ Botolan ຂອງ ສົມບັດ.
ພາສາ Abellen: Abellen , Abenlen , Aburlin, ຫຼື Ayta Abellen ແມ່ນພາສາ Sambalic. ມັນມີຜູ້ເວົ້າປະມານ 3500 ຄົນແລະເວົ້າໃນຊຸມຊົນ Aeta ໃນແຂວງ Tarlac, ປະເທດຟີລິບປິນ Ayta Abellen ເອງແມ່ນສ່ວນ ໜຶ່ງ ຂອງຄອບຄົວພາສາ Sambalic ໃນປະເທດຟີລິບປິນແລະມີຄວາມກ່ຽວຂ້ອງຢ່າງໃກ້ຊິດບໍ່ພຽງແຕ່ 5 ພາສາອື່ນໆຂອງ Ayta, ແຕ່ຍັງມີພາສາເວົ້າຂອງ Botolan ຂອງ ສົມບັດ.
Leonardo Abelenda: Leonardo Daniel Abelenda Rodríguez ແມ່ນນັກບານເຕະຊາວ Uruguayan ປະຈຸບັນ ກຳ ລັງຫລິ້ນໃຫ້ Plaza Colonia ໃນ Uruguayan Segunda División.
Leonardo Abelenda: Leonardo Daniel Abelenda Rodríguez ແມ່ນນັກບານເຕະຊາວ Uruguayan ປະຈຸບັນ ກຳ ລັງຫລິ້ນໃຫ້ Plaza Colonia ໃນ Uruguayan Segunda División.
Abelemkpe: ເມືອງ Abelenkpe ແມ່ນເຂດຕົວເມືອງໃນເມືອງ Accra Metropolitan, ເຊິ່ງເປັນເມືອງ ໜຶ່ງ ຂອງເຂດ Greater Accra ໃນປະເທດການາ.
Jim Abeler: James J. Abeler II ແມ່ນນັກການເມືອງລັດມິນນິໂຊຕາແລະເປັນສະມາຊິກສະພາແຫ່ງລັດມິນນີໂຊຕາ. ສະມາຊິກຂອງພັກຣີພັບບລີກັນຂອງລັດມິນນິໂຊຕາ, ທ່ານເປັນຕົວແທນໃຫ້ແກ່ເຂດ 35 ໃນເຂດເມືອງຄູ່ເມືອງທາງພາກ ເໜືອ. ໃນເມື່ອກ່ອນລາວເຄີຍເປັນຕົວແທນເຂດ 35A ໃນສະພາຜູ້ແທນລັດ Minnesota.
Jim Abeler: James J. Abeler II ແມ່ນນັກການເມືອງລັດມິນນິໂຊຕາແລະເປັນສະມາຊິກສະພາແຫ່ງລັດມິນນີໂຊຕາ. ສະມາຊິກຂອງພັກຣີພັບບລີກັນຂອງລັດມິນນິໂຊຕາ, ທ່ານເປັນຕົວແທນໃຫ້ແກ່ເຂດ 35 ໃນເຂດເມືອງຄູ່ເມືອງທາງພາກ ເໜືອ. ໃນເມື່ອກ່ອນລາວເຄີຍເປັນຕົວແທນເຂດ 35A ໃນສະພາຜູ້ແທນລັດ Minnesota.
Abeles: Abeles ແມ່ນນາມສະກຸນພາສາອັງກິດແລະຢິວ, ມາຈາກຊື່ໃນພຣະຄໍາພີ Abel. ບຸກຄົນທີ່ມີຊື່ສຽງປະກອບມີ: Benjamin Abeles, ນັກຟີຊິກສາດຂອງອາເມລິກາ Edward Abeles (1869–1919), ນັກສະແດງຊາວອາເມລິກາ Florin Abelès (1922-2005), ນັກຟິຊິກສາດຝຣັ່ງ John H Abeles, ນັກທຸລະກິດອາເມລິກາ Kim Victoria Abeles, ນັກສິລະປິນອາເມລິກາ ນາງ Michele Abeles, ນັກສິລະປິນອາເມລິກາ Peter Abeles (ປີ 1924991999), ນັກທຸລະກິດອົດສະຕາລີ Moshe Abeles, ນັກຄົ້ນຄວ້າສະ ໝອງ ຂອງອິດສະຣາເອນ Norman Abeles, ນັກຈິດຕະສາດອາເມລິກາທີ່ເກີດມາຈາກອອສເຕີຍ ນາງ Ruth Abeles, ນັກກິລາໂອລິມປິກໂອລິມປິກຂອງອິສຣາແອລ Sigmund Abeles, ນັກແຕ້ມຮູບຄົນອາເມລິກາ
Benjamin Abeles: Benjamin Abeles ແມ່ນນັກຟີຊິກສາດດ້ານອອສເຕີຍ - ເຊັກເຊິ່ງມີການຄົ້ນຄວ້າໃນປີ 1960 ໃນສະຫະລັດກ່ຽວກັບໂລຫະປະສົມຊິລິໂຄນ ium ໃນພາຫະນະເຕັກໂນໂລຢີທີ່ ນຳ ໃຊ້ເຕັກໂນໂລຢີທີ່ໃຊ້ໃນການສືບສວນພະລັງງານເຊັ່ນ ຍານອະວະກາດ Voyager . ລາວເຕີບໃຫຍ່ຢູ່ໃນອອສເຕີຍແລະເຊັກໂກສະໂລວາກີແລະໄດ້ມາຮອດອັງກິດໃນປີ 1939 ໃນພາລະກິດ ໜຶ່ງ ຂອງ Kindertransport . ລາວຈົບການສຶກສາຫຼັງສົງຄາມຢູ່ເຊັກໂກສະໂລວາກີແລະອິດສະຣາເອນ, ໄດ້ຮັບປະລິນຍາເອກດ້ານຟີຊິກສາດ. ຈາກນັ້ນລາວໄດ້ ດຳ ລົງຊີວິດແລະເຮັດວຽກເປັນນັກວິສະວະ ກຳ ຄົ້ນຄ້ວາຢູ່ສະຫະລັດອາເມລິກາແລະໄດ້ ບຳ ນານໃນປີ 1995. ກຽດຕິຍົດຂອງລາວລວມມີ Medal Ballantine Medal ປີ 1979 ແລະການປະດິດເຂົ້າໄປໃນ New Jersey Inventors Hall of Fame (1991).
Peter Abeles: Sir Peter Emil Herbert Abeles , AC ແມ່ນມະຫາເສດຖີດ້ານການຂົນສົ່ງຂອງອົດສະຕາລີ. ຊາວອົບພະຍົບຈາກປະເທດຮັງກາຣີ, ລາວໄດ້ກາຍເປັນນັກທຸລະກິດຢູ່ປະເທດອົດສະຕາລີ, ແລະລາວໄດ້ເປັນສະມາຊິກໃນປີ 1972.
ວິທີການໂອນຍ້າຍມາຕຣິກເບື້ອງ (optics): ວິທີການໂອນຍ້າຍ - ມາຕຣິກເບື້ອງ ແມ່ນວິທີການທີ່ໃຊ້ໃນການ ນຳ ໃຊ້ສາຍແສງແລະສຽງ ສຳ ລັບວິເຄາະການຂະຫຍາຍພັນຂອງຄື້ນໄຟຟ້າຫລືຄື້ນສຽງໂດຍຜ່ານສື່ກາງ. ນີ້ແມ່ນຕົວຢ່າງທີ່ກ່ຽວຂ້ອງກັບການອອກແບບຂອງການເຄືອບຕ້ານການສະທ້ອນແສງແລະກະຈົກປ້ອງກັນແສງ.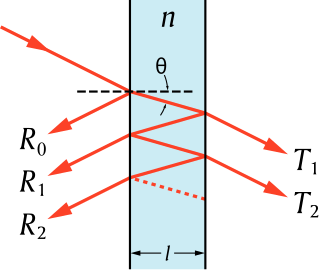
Abalessa: ເມືອງ Abalessa ແມ່ນເມືອງ ໜຶ່ງ ແລະເປັນບ້ານ ໜຶ່ງ ໃນແຂວງ Tamanrasset, ໃນພາກໃຕ້ຂອງປະເທດ Algeria, ເປັນເຂດທີ່ມີການຮ່ວມມືກັບເມືອງທີ່ມີຊື່ດຽວກັນ. ອີງຕາມການ ສຳ ຫລວດ ສຳ ມະໂນຄົວປີ 2008 ມັນມີປະຊາກອນ 9,163 ຄົນທຽບໃສ່ປີ 6,484, ເຊິ່ງມີອັດຕາການເຕີບໂຕປະ ຈຳ ປີ 3,6%. ເມືອງ Abalessa ຕັ້ງຢູ່ຕາມເສັ້ນທາງການຄ້າ Trans-Saharan ວັດຖຸບູຮານ, 80 ກິໂລແມັດ (50 ໄມ) ທິດຕາເວັນຕົກຂອງເມືອງ Tamanrasset, ນະຄອນຫຼວງຂອງແຂວງ. ລະຫັດໄປສະນີຂອງເມືອງແມ່ນ 11120.
Abalessa: ເມືອງ Abalessa ແມ່ນເມືອງ ໜຶ່ງ ແລະເປັນບ້ານ ໜຶ່ງ ໃນແຂວງ Tamanrasset, ໃນພາກໃຕ້ຂອງປະເທດ Algeria, ເປັນເຂດທີ່ມີການຮ່ວມມືກັບເມືອງທີ່ມີຊື່ດຽວກັນ. ອີງຕາມການ ສຳ ຫລວດ ສຳ ມະໂນຄົວປີ 2008 ມັນມີປະຊາກອນ 9,163 ຄົນທຽບໃສ່ປີ 6,484, ເຊິ່ງມີອັດຕາການເຕີບໂຕປະ ຈຳ ປີ 3,6%. ເມືອງ Abalessa ຕັ້ງຢູ່ຕາມເສັ້ນທາງການຄ້າ Trans-Saharan ວັດຖຸບູຮານ, 80 ກິໂລແມັດ (50 ໄມ) ທິດຕາເວັນຕົກຂອງເມືອງ Tamanrasset, ນະຄອນຫຼວງຂອງແຂວງ. ລະຫັດໄປສະນີຂອງເມືອງແມ່ນ 11120.
Johann Philipp Abelin: Johann Philipp Abelin ແມ່ນນັກພະຍາດເຍີລະມະນີຊາວເຢຍລະມັນທີ່ມີອາຊີບຍ້ອຍຕົວໃນສະຕະວັດທີ 16 ແລະ 17. ລາວໄດ້ເກີດ, ອາດຈະຢູ່ທີ່ Strasbourg, ແລະໄດ້ເສຍຊີວິດຢູ່ທີ່ນັ້ນໃນລະຫວ່າງປີ 1634 ແລະ 1637. ລາວໄດ້ຂຽນປະຫວັດສາດຫຼາຍໆຢ່າງພາຍໃຕ້ການຂຽນຂອງ Abeleus , Philipp Arlanibäus , Johann Ludwig Gottfried ແລະ Gotofredus .
tataira Oxytrigona: Oxytrigona tataira , ທີ່ຮູ້ກັນທົ່ວໄປວ່າ tataíra ຫຼື abelha-de-fogo , ແມ່ນຊະນິດຂອງເຜິ້ງທີ່ບໍ່ຮູ້ສຶກຕົວໃນຄອບຄົວ Apidae ແລະຊົນເຜົ່າ Meliponini.
Abelhaleem Hasan Abdelraziq Ashqar: Abelhaleem Hasan Abdelraziq Ashqar ແມ່ນນັກເຄື່ອນໄຫວຊາວມຸດສະລິມຊາວປາແລສໄຕນ໌, ເຊິ່ງເປັນຜູ້ຊ່ວຍຄູອາຈານສອນທຸລະກິດຢູ່ມະຫາວິທະຍາໄລ Howard. ລາວໄດ້ຖືກຕັດສິນວ່າຖືກກ່າວຫາດູຖູກແລະຂັດຂວາງຄວາມຍຸຕິ ທຳ ສຳ ລັບການປະຕິເສດທີ່ຈະເປັນພະຍານຕໍ່ຄະນະຕຸລາການໃຫຍ່ໃນການທົດລອງທີ່ກ່ຽວຂ້ອງກັບການສະ ໜັບ ສະ ໜູນ ຂອງອົງການຮາມາສໂດຍຜູ້ໃຫ້ທຶນຢູ່ສະຫະລັດອາເມລິກາ, ແລະໄດ້ຖືກຕັດສິນໂທດໃນເດືອນພະຈິກປີ 2007 ຈຳ ຄຸກ 135 ເດືອນ.
Abelhaleem Hasan Abdelraziq Ashqar: Abelhaleem Hasan Abdelraziq Ashqar ແມ່ນນັກເຄື່ອນໄຫວຊາວມຸດສະລິມຊາວປາແລສໄຕນ໌, ເຊິ່ງເປັນຜູ້ຊ່ວຍຄູອາຈານສອນທຸລະກິດຢູ່ມະຫາວິທະຍາໄລ Howard. ລາວໄດ້ຖືກຕັດສິນວ່າຖືກກ່າວຫາດູຖູກແລະຂັດຂວາງຄວາມຍຸຕິ ທຳ ສຳ ລັບການປະຕິເສດທີ່ຈະເປັນພະຍານຕໍ່ຄະນະຕຸລາການໃຫຍ່ໃນການທົດລອງທີ່ກ່ຽວຂ້ອງກັບການສະ ໜັບ ສະ ໜູນ ຂອງອົງການຮາມາສໂດຍຜູ້ໃຫ້ທຶນຢູ່ສະຫະລັດອາເມລິກາ, ແລະໄດ້ຖືກຕັດສິນໂທດໃນເດືອນພະຈິກປີ 2007 ຈຳ ຄຸກ 135 ເດືອນ.
Abelheira: Abelheira ແມ່ນ ໝູ່ ບ້ານ ໜຶ່ງ ໃນເທດສະບານLourinhãຂອງປະເທດ Portugal.
ເມືອງ Parish: Parbeļi Parish ແມ່ນ ໜ່ວຍ ງານບໍລິຫານຂອງເທດສະບານ Jēkabpils , ລັດເວຍ.
ເມືອງ Parish: Parbeļi Parish ແມ່ນ ໜ່ວຍ ງານບໍລິຫານຂອງເທດສະບານ Jēkabpils , ລັດເວຍ.
Abelia: Abelia ແມ່ນສະກຸນທີ່ໄດ້ຮັບການຍອມຮັບໃນເມື່ອກ່ອນເຊິ່ງປະກອບມີປະມານ 30 ຊະນິດແລະປະສົມ, ຖືກຈັດໃສ່ໃນຄອບຄົວ honeysuckle, Caprifoliaceae. ການສຶກສາກ່ຽວກັບທາດໂມເລກຸນໄດ້ສະແດງໃຫ້ເຫັນວ່າສະກຸນດັ່ງກ່າວບໍ່ແມ່ນ monophyletic, ແລະໃນປີ 2013, Maarten Christenhusz ໄດ້ສະ ເໜີ ການລວມຕົວຂອງ Abelia ເຂົ້າໄປໃນ Linnaea , ພ້ອມດ້ວຍຜະລິດຕະພັນອື່ນໆ. ພາກສ່ວນ Abelia Zabelia ໄດ້ຖືກຍົກຂຶ້ນມາເປັນສະກຸນ Zabelia .
Abelia (ອົງການຈັດຕັ້ງ): Abelia ແມ່ນອົງການຈັດຕັ້ງຂອງຜູ້ໃຊ້ແຮງງານໃນປະເທດນໍເວ, ຈັດຕັ້ງຂື້ນພາຍໃຕ້ສະຫະພັນແຫ່ງຊາດຂອງວິສາຫະກິດນອກແວ.
Abelia (ອົງການຈັດຕັ້ງ): Abelia ແມ່ນອົງການຈັດຕັ້ງຂອງຜູ້ໃຊ້ແຮງງານໃນປະເທດນໍເວ, ຈັດຕັ້ງຂື້ນພາຍໃຕ້ສະຫະພັນແຫ່ງຊາດຂອງວິສາຫະກິດນອກແວ.
Linnaea chinensis: Linnaea chinensis , ຄຳ ສັບຄ້າຍຄື Abelia chinensis ແລະ Abelia rupestris , ແມ່ນຊະນິດຂອງຕົ້ນດອກໄມ້ໃນຕະກູນ honeysuckle Caprifoliaceae. ມັນໄດ້ຖືກອະທິບາຍໂດຍ Robert Brown ໃນປີ 1818, ແລະຖືກໂອນໄປຫາສະກຸນ Linnaea ໃນປີ 1872, ເຖິງແມ່ນວ່າການເຄື່ອນໄຫວນີ້ບໍ່ໄດ້ຖືກຍອມຮັບຢ່າງກວ້າງຂວາງຈົນເຖິງປີ 2013. ໂຮງງານດັ່ງກ່າວອາໄສຢູ່ໃນປະເທດຈີນ, ໄຕ້ຫວັນແລະຍີ່ປຸ່ນ. ມັນເປັນໄມ້ພຸ່ມປະສົມປ່ຽນໃບທີ່ມີໃບສີແດງແລະໃບເຫຼື້ອມເປັນເງົາ, ໃບນ້ອຍໆກາຍເປັນສີນ້ ຳ ຕານແດງກ່ອນລະດູໃບໄມ້ປົ່ງ. ມັນແມ່ນ ໜຶ່ງ ໃນບັນດາຊະນິດທີ່ທົນທານຕໍ່ເຢັນຫຼາຍທີ່ສຸດພາຍໃນສະກຸນ.
Linnaea chinensis: Linnaea chinensis , ຄຳ ສັບຄ້າຍຄື Abelia chinensis ແລະ Abelia rupestris , ແມ່ນຊະນິດຂອງຕົ້ນດອກໄມ້ໃນຕະກູນ honeysuckle Caprifoliaceae. ມັນໄດ້ຖືກອະທິບາຍໂດຍ Robert Brown ໃນປີ 1818, ແລະຖືກໂອນໄປຫາສະກຸນ Linnaea ໃນປີ 1872, ເຖິງແມ່ນວ່າການເຄື່ອນໄຫວນີ້ບໍ່ໄດ້ຖືກຍອມຮັບຢ່າງກວ້າງຂວາງຈົນເຖິງປີ 2013. ໂຮງງານດັ່ງກ່າວອາໄສຢູ່ໃນປະເທດຈີນ, ໄຕ້ຫວັນແລະຍີ່ປຸ່ນ. ມັນເປັນໄມ້ພຸ່ມປະສົມປ່ຽນໃບທີ່ມີໃບສີແດງແລະໃບເຫຼື້ອມເປັນເງົາ, ໃບນ້ອຍໆກາຍເປັນສີນ້ ຳ ຕານແດງກ່ອນລະດູໃບໄມ້ປົ່ງ. ມັນແມ່ນ ໜຶ່ງ ໃນບັນດາຊະນິດທີ່ທົນທານຕໍ່ເຢັນຫຼາຍທີ່ສຸດພາຍໃນສະກຸນ.
Linnaea chinensis: Linnaea chinensis , ຄຳ ສັບຄ້າຍຄື Abelia chinensis ແລະ Abelia rupestris , ແມ່ນຊະນິດຂອງຕົ້ນດອກໄມ້ໃນຕະກູນ honeysuckle Caprifoliaceae. ມັນໄດ້ຖືກອະທິບາຍໂດຍ Robert Brown ໃນປີ 1818, ແລະຖືກໂອນໄປຫາສະກຸນ Linnaea ໃນປີ 1872, ເຖິງແມ່ນວ່າການເຄື່ອນໄຫວນີ້ບໍ່ໄດ້ຖືກຍອມຮັບຢ່າງກວ້າງຂວາງຈົນເຖິງປີ 2013. ໂຮງງານດັ່ງກ່າວອາໄສຢູ່ໃນປະເທດຈີນ, ໄຕ້ຫວັນແລະຍີ່ປຸ່ນ. ມັນເປັນໄມ້ພຸ່ມປະສົມປ່ຽນໃບທີ່ມີໃບສີແດງແລະໃບເຫຼື້ອມເປັນເງົາ, ໃບນ້ອຍໆກາຍເປັນສີນ້ ຳ ຕານແດງກ່ອນລະດູໃບໄມ້ປົ່ງ. ມັນແມ່ນ ໜຶ່ງ ໃນບັນດາຊະນິດທີ່ທົນທານຕໍ່ເຢັນຫຼາຍທີ່ສຸດພາຍໃນສະກຸນ.
ໂບດ Abelia: ໂບດ Abelia ຂອງ Trinity ແມ່ນໂບດ Georgian Orthodox ໃນສະຕະວັດທີ 13, ຕັ້ງຢູ່ເທດສະບານ Tetri Tsqaro ໃນພາກໃຕ້ - ພາກກາງຂອງປະເທດ Georgia, ເຂດ Kvemo Kartli. ການອອກແບບແບບດ່ຽວໆແບບ ທຳ ມະດາ, ມັນຕັ້ງຢູ່ດ້ານນອກຂອງບ້ານ Abeliani ທີ່ທັນສະໄຫມ, ເຊິ່ງເອີ້ນວ່າ Abelia. ເອກະສານອ້າງອີງເຖິງຄວາມຂີ້ຕົວະໃນປະເທດຈໍເຈຍພາຍໃຕ້ກົດລະບຽບຂອງມົງໂກລີໃນແຜ່ນຈາລຶກຢູ່ຝາທາງໃຕ້ຂອງໂບດເຮັດໃຫ້ມັນສາມາດຮອດປະຈຸບັນການກໍ່ສ້າງຮອດໄລຍະ 1250–1259 ໂບດຖືກຈາລຶກໃສ່ບັນຊີລາຍຊື່ຂອງອະນຸສາວະລີວັດທະນະ ທຳ ທີ່ບໍ່ຫວັ່ນໄຫວກ່ຽວກັບຄວາມ ສຳ ຄັນຂອງຊາດຂອງຈໍເຈຍ.
Zabelia corymbosa: Zabelia corymbosa ແມ່ນພືດດອກໄມ້ຊະນິດ ໜຶ່ງ ໃນຄອບຄົວ honeysuckle, Caprifoliaceae. ມັນມີຖິ່ນ ກຳ ເນີດຢູ່ອາຊີກາງ, ບ່ອນທີ່ມັນເກີດຂື້ນຢູ່ປະເທດຄາຊັກສະຖານ, Kyrgyzstan, ແລະ Tajikistan.
Linnaea spathulata: Linnaea spathulata , ຄຳ ສັບຄ້າຍຄື Abelia spathulata , ແມ່ນຊະນິດຂອງ Linnaea ໃນຄອບຄົວ honeysuckle (Caprifoliaceae). ໂຮງງານດັ່ງກ່າວແມ່ນແຜ່ລາມໄປທົ່ວປະເທດເກົາຫຼີແລະຍີ່ປຸ່ນ.
Linnaea floribunda: Linnaea floribunda ແມ່ນພືດດອກໄມ້ຊະນິດ ໜຶ່ງ ໃນຄອບຄົວ honeysuckle, Caprifoliaceae, ທີ່ມີຖິ່ນ ກຳ ເນີດມາຈາກປະເທດແມັກຊິໂກ. ເຕີບໃຫຍ່ເຖິງ 4 ມ (13 ຟຸດ) ສູງແລະກວ້າງ, ມັນເປັນໄມ້ພຸ່ມເຄິ່ງຂຽວຫລືຂຽວຕະຫຼອດປີທີ່ມີໃບຮູບໄຂ່ເຫຼື້ອມແລະເປັນກຸ່ມທີ່ມີດອກໄມ້ cerise tubular ເຖິງ 5 ຊມ (2.0 ໃນ) ຍາວ. ເຖິງແມ່ນວ່າ hardy ລົງເຖິງ −10 ° C (14 ° F) ມັນມັກສະຖານທີ່ທີ່ພັກອາໄສ, ຍົກຕົວຢ່າງຕໍ່ກັບກໍາແພງຫີນທີ່ຫັນ ໜ້າ ໄປທາງທິດໃຕ້.
Linnaea × grandiflora: Linnaea × grandiflora , ຄຳ ສັບຄ້າຍຄື Abelia × grandiflora , ແມ່ນພືດປະສົມຂອງດອກໄມ້ປະສົມໃນຄອບຄົວ honeysuckle Caprifoliaceae, ລ້ຽງໂດຍການປະສົມ L. chinensis ກັບ L. uniflora .
Linnaea chinensis: Linnaea chinensis , ຄຳ ສັບຄ້າຍຄື Abelia chinensis ແລະ Abelia rupestris , ແມ່ນຊະນິດຂອງຕົ້ນດອກໄມ້ໃນຕະກູນ honeysuckle Caprifoliaceae. ມັນໄດ້ຖືກອະທິບາຍໂດຍ Robert Brown ໃນປີ 1818, ແລະຖືກໂອນໄປຫາສະກຸນ Linnaea ໃນປີ 1872, ເຖິງແມ່ນວ່າການເຄື່ອນໄຫວນີ້ບໍ່ໄດ້ຖືກຍອມຮັບຢ່າງກວ້າງຂວາງຈົນເຖິງປີ 2013. ໂຮງງານດັ່ງກ່າວອາໄສຢູ່ໃນປະເທດຈີນ, ໄຕ້ຫວັນແລະຍີ່ປຸ່ນ. ມັນເປັນໄມ້ພຸ່ມປະສົມປ່ຽນໃບທີ່ມີໃບສີແດງແລະໃບເຫຼື້ອມເປັນເງົາ, ໃບນ້ອຍໆກາຍເປັນສີນ້ ຳ ຕານແດງກ່ອນລະດູໃບໄມ້ປົ່ງ. ມັນແມ່ນ ໜຶ່ງ ໃນບັນດາຊະນິດທີ່ທົນທານຕໍ່ເຢັນຫຼາຍທີ່ສຸດພາຍໃນສະກຸນ.
Linnaea floribunda: Linnaea floribunda ແມ່ນພືດດອກໄມ້ຊະນິດ ໜຶ່ງ ໃນຄອບຄົວ honeysuckle, Caprifoliaceae, ທີ່ມີຖິ່ນ ກຳ ເນີດມາຈາກປະເທດແມັກຊິໂກ. ເຕີບໃຫຍ່ເຖິງ 4 ມ (13 ຟຸດ) ສູງແລະກວ້າງ, ມັນເປັນໄມ້ພຸ່ມເຄິ່ງຂຽວຫລືຂຽວຕະຫຼອດປີທີ່ມີໃບຮູບໄຂ່ເຫຼື້ອມແລະເປັນກຸ່ມທີ່ມີດອກໄມ້ cerise tubular ເຖິງ 5 ຊມ (2.0 ໃນ) ຍາວ. ເຖິງແມ່ນວ່າ hardy ລົງເຖິງ −10 ° C (14 ° F) ມັນມັກສະຖານທີ່ທີ່ພັກອາໄສ, ຍົກຕົວຢ່າງຕໍ່ກັບກໍາແພງຫີນທີ່ຫັນ ໜ້າ ໄປທາງທິດໃຕ້.
Linnaea chinensis: Linnaea chinensis , ຄຳ ສັບຄ້າຍຄື Abelia chinensis ແລະ Abelia rupestris , ແມ່ນຊະນິດຂອງຕົ້ນດອກໄມ້ໃນຕະກູນ honeysuckle Caprifoliaceae. ມັນໄດ້ຖືກອະທິບາຍໂດຍ Robert Brown ໃນປີ 1818, ແລະຖືກໂອນໄປຫາສະກຸນ Linnaea ໃນປີ 1872, ເຖິງແມ່ນວ່າການເຄື່ອນໄຫວນີ້ບໍ່ໄດ້ຖືກຍອມຮັບຢ່າງກວ້າງຂວາງຈົນເຖິງປີ 2013. ໂຮງງານດັ່ງກ່າວອາໄສຢູ່ໃນປະເທດຈີນ, ໄຕ້ຫວັນແລະຍີ່ປຸ່ນ. ມັນເປັນໄມ້ພຸ່ມປະສົມປ່ຽນໃບທີ່ມີໃບສີແດງແລະໃບເຫຼື້ອມເປັນເງົາ, ໃບນ້ອຍໆກາຍເປັນສີນ້ ຳ ຕານແດງກ່ອນລະດູໃບໄມ້ປົ່ງ. ມັນແມ່ນ ໜຶ່ງ ໃນບັນດາຊະນິດທີ່ທົນທານຕໍ່ເຢັນຫຼາຍທີ່ສຸດພາຍໃນສະກຸນ.
Linnaea spathulata: Linnaea spathulata , ຄຳ ສັບຄ້າຍຄື Abelia spathulata , ແມ່ນຊະນິດຂອງ Linnaea ໃນຄອບຄົວ honeysuckle (Caprifoliaceae). ໂຮງງານດັ່ງກ່າວແມ່ນແຜ່ລາມໄປທົ່ວປະເທດເກົາຫຼີແລະຍີ່ປຸ່ນ.
Linnaea chinensis: Linnaea chinensis , ຄຳ ສັບຄ້າຍຄື Abelia chinensis ແລະ Abelia rupestris , ແມ່ນຊະນິດຂອງຕົ້ນດອກໄມ້ໃນຕະກູນ honeysuckle Caprifoliaceae. ມັນໄດ້ຖືກອະທິບາຍໂດຍ Robert Brown ໃນປີ 1818, ແລະຖືກໂອນໄປຫາສະກຸນ Linnaea ໃນປີ 1872, ເຖິງແມ່ນວ່າການເຄື່ອນໄຫວນີ້ບໍ່ໄດ້ຖືກຍອມຮັບຢ່າງກວ້າງຂວາງຈົນເຖິງປີ 2013. ໂຮງງານດັ່ງກ່າວອາໄສຢູ່ໃນປະເທດຈີນ, ໄຕ້ຫວັນແລະຍີ່ປຸ່ນ. ມັນເປັນໄມ້ພຸ່ມປະສົມປ່ຽນໃບທີ່ມີໃບສີແດງແລະໃບເຫຼື້ອມເປັນເງົາ, ໃບນ້ອຍໆກາຍເປັນສີນ້ ຳ ຕານແດງກ່ອນລະດູໃບໄມ້ປົ່ງ. ມັນແມ່ນ ໜຶ່ງ ໃນບັນດາຊະນິດທີ່ທົນທານຕໍ່ເຢັນຫຼາຍທີ່ສຸດພາຍໃນສະກຸນ.
Linnaea parvifolia: Linnaea parvifolia , ຄຳ ສັບຄ້າຍຄື Abelia schumannii , ແມ່ນຊະນິດຂອງຕົ້ນດອກໄມ້ໃນຄອບຄົວ Caprifoliaceae, ທີ່ມີຖິ່ນ ກຳ ເນີດຢູ່ພາກກາງຂອງປະເທດຈີນ. ມັນເປັນໄມ້ພຸ່ມເຄິ່ງຂຽວຕະຫລອດປີສູງເຖິງ 2 ມ (7 ຟຸດ) ໂດຍສູງ 3 ມ (10 ຟຸດ) ກວ້າງ. ດອກກຸຫລາບທີ່ມີກາບດອກສີແດງຖືກຜະລິດໃນລະດູຮ້ອນແລະລະດູໃບໄມ້ປົ່ງ.
Linnaea parvifolia: Linnaea parvifolia , ຄຳ ສັບຄ້າຍຄື Abelia schumannii , ແມ່ນຊະນິດຂອງຕົ້ນດອກໄມ້ໃນຄອບຄົວ Caprifoliaceae, ທີ່ມີຖິ່ນ ກຳ ເນີດຢູ່ພາກກາງຂອງປະເທດຈີນ. ມັນເປັນໄມ້ພຸ່ມເຄິ່ງຂຽວຕະຫລອດປີສູງເຖິງ 2 ມ (7 ຟຸດ) ໂດຍສູງ 3 ມ (10 ຟຸດ) ກວ້າງ. ດອກກຸຫລາບທີ່ມີກາບດອກສີແດງຖືກຜະລິດໃນລະດູຮ້ອນແລະລະດູໃບໄມ້ປົ່ງ.
tyaihyonii Zabelia: Zabelia tyaihyonii , ຄຳ ສັບຄ້າຍຄື Abelia mosanensis , ທີ່ຮູ້ກັນໃນນາມ abelia ທີ່ມີກິ່ນຫອມ , ແມ່ນຊະນິດຂອງຕົ້ນໄມ້ປ່ຽນໃບໃນຄອບຄົວ Caprifoliaceae honeysuckle. ເຕີບໃຫຍ່ສູງເຖິງ 2 ແມັດແລະກວ້າງ, ມັນແຂງກ່ວາຊະນິດທີ່ກ່ຽວຂ້ອງ, ມີອຸນຫະພູມທີ່ມີຊີວິດລອດຕໍ່າເຖິງ −20 ° C (°4° F). ດອກໄມ້ເປັນຫຼອດເປັນສີຂາວແກມສີບົວແລະມີກິ່ນຫອມສູງ, ປະກົດອອກໃນທ້າຍລະດູໃບໄມ້ປົ່ງ. ໃບສີຂຽວເຫຼື້ອມເປັນສີແດງໃນລະດູໃບໄມ້ປົ່ງກ່ອນທີ່ຈະຕົກ.
Linnaea parvifolia: Linnaea parvifolia , ຄຳ ສັບຄ້າຍຄື Abelia schumannii , ແມ່ນຊະນິດຂອງຕົ້ນດອກໄມ້ໃນຄອບຄົວ Caprifoliaceae, ທີ່ມີຖິ່ນ ກຳ ເນີດຢູ່ພາກກາງຂອງປະເທດຈີນ. ມັນເປັນໄມ້ພຸ່ມເຄິ່ງຂຽວຕະຫລອດປີສູງເຖິງ 2 ມ (7 ຟຸດ) ໂດຍສູງ 3 ມ (10 ຟຸດ) ກວ້າງ. ດອກກຸຫລາບທີ່ມີກາບດອກສີແດງຖືກຜະລິດໃນລະດູຮ້ອນແລະລະດູໃບໄມ້ປົ່ງ.
Linnaea parvifolia: Linnaea parvifolia , ຄຳ ສັບຄ້າຍຄື Abelia schumannii , ແມ່ນຊະນິດຂອງຕົ້ນດອກໄມ້ໃນຄອບຄົວ Caprifoliaceae, ທີ່ມີຖິ່ນ ກຳ ເນີດຢູ່ພາກກາງຂອງປະເທດຈີນ. ມັນເປັນໄມ້ພຸ່ມເຄິ່ງຂຽວຕະຫລອດປີສູງເຖິງ 2 ມ (7 ຟຸດ) ໂດຍສູງ 3 ມ (10 ຟຸດ) ກວ້າງ. ດອກກຸຫລາບທີ່ມີກາບດອກສີແດງຖືກຜະລິດໃນລະດູຮ້ອນແລະລະດູໃບໄມ້ປົ່ງ.
Linnaea chinensis: Linnaea chinensis , ຄຳ ສັບຄ້າຍຄື Abelia chinensis ແລະ Abelia rupestris , ແມ່ນຊະນິດຂອງຕົ້ນດອກໄມ້ໃນຕະກູນ honeysuckle Caprifoliaceae. ມັນໄດ້ຖືກອະທິບາຍໂດຍ Robert Brown ໃນປີ 1818, ແລະຖືກໂອນໄປຫາສະກຸນ Linnaea ໃນປີ 1872, ເຖິງແມ່ນວ່າການເຄື່ອນໄຫວນີ້ບໍ່ໄດ້ຖືກຍອມຮັບຢ່າງກວ້າງຂວາງຈົນເຖິງປີ 2013. ໂຮງງານດັ່ງກ່າວອາໄສຢູ່ໃນປະເທດຈີນ, ໄຕ້ຫວັນແລະຍີ່ປຸ່ນ. ມັນເປັນໄມ້ພຸ່ມປະສົມປ່ຽນໃບທີ່ມີໃບສີແດງແລະໃບເຫຼື້ອມເປັນເງົາ, ໃບນ້ອຍໆກາຍເປັນສີນ້ ຳ ຕານແດງກ່ອນລະດູໃບໄມ້ປົ່ງ. ມັນແມ່ນ ໜຶ່ງ ໃນບັນດາຊະນິດທີ່ທົນທານຕໍ່ເຢັນຫຼາຍທີ່ສຸດພາຍໃນສະກຸນ.
Linnaea spathulata: Linnaea spathulata , ຄຳ ສັບຄ້າຍຄື Abelia spathulata , ແມ່ນຊະນິດຂອງ Linnaea ໃນຄອບຄົວ honeysuckle (Caprifoliaceae). ໂຮງງານດັ່ງກ່າວແມ່ນແຜ່ລາມໄປທົ່ວປະເທດເກົາຫຼີແລະຍີ່ປຸ່ນ.
Linnaea parvifolia: Linnaea parvifolia , ຄຳ ສັບຄ້າຍຄື Abelia schumannii , ແມ່ນຊະນິດຂອງຕົ້ນດອກໄມ້ໃນຄອບຄົວ Caprifoliaceae, ທີ່ມີຖິ່ນ ກຳ ເນີດຢູ່ພາກກາງຂອງປະເທດຈີນ. ມັນເປັນໄມ້ພຸ່ມເຄິ່ງຂຽວຕະຫລອດປີສູງເຖິງ 2 ມ (7 ຟຸດ) ໂດຍສູງ 3 ມ (10 ຟຸດ) ກວ້າງ. ດອກກຸຫລາບທີ່ມີກາບດອກສີແດງຖືກຜະລິດໃນລະດູຮ້ອນແລະລະດູໃບໄມ້ປົ່ງ.
Linnaea parvifolia: Linnaea parvifolia , ຄຳ ສັບຄ້າຍຄື Abelia schumannii , ແມ່ນຊະນິດຂອງຕົ້ນດອກໄມ້ໃນຄອບຄົວ Caprifoliaceae, ທີ່ມີຖິ່ນ ກຳ ເນີດຢູ່ພາກກາງຂອງປະເທດຈີນ. ມັນເປັນໄມ້ພຸ່ມເຄິ່ງຂຽວຕະຫລອດປີສູງເຖິງ 2 ມ (7 ຟຸດ) ໂດຍສູງ 3 ມ (10 ຟຸດ) ກວ້າງ. ດອກກຸຫລາບທີ່ມີກາບດອກສີແດງຖືກຜະລິດໃນລະດູຮ້ອນແລະລະດູໃບໄມ້ປົ່ງ.
Linnaea spathulata: Linnaea spathulata , ຄຳ ສັບຄ້າຍຄື Abelia spathulata , ແມ່ນຊະນິດຂອງ Linnaea ໃນຄອບຄົວ honeysuckle (Caprifoliaceae). ໂຮງງານດັ່ງກ່າວແມ່ນແຜ່ລາມໄປທົ່ວປະເທດເກົາຫຼີແລະຍີ່ປຸ່ນ.
Linnaea floribunda: Linnaea floribunda ແມ່ນພືດດອກໄມ້ຊະນິດ ໜຶ່ງ ໃນຄອບຄົວ honeysuckle, Caprifoliaceae, ທີ່ມີຖິ່ນ ກຳ ເນີດມາຈາກປະເທດແມັກຊິໂກ. ເຕີບໃຫຍ່ເຖິງ 4 ມ (13 ຟຸດ) ສູງແລະກວ້າງ, ມັນເປັນໄມ້ພຸ່ມເຄິ່ງຂຽວຫລືຂຽວຕະຫຼອດປີທີ່ມີໃບຮູບໄຂ່ເຫຼື້ອມແລະເປັນກຸ່ມທີ່ມີດອກໄມ້ cerise tubular ເຖິງ 5 ຊມ (2.0 ໃນ) ຍາວ. ເຖິງແມ່ນວ່າ hardy ລົງເຖິງ −10 ° C (14 ° F) ມັນມັກສະຖານທີ່ທີ່ພັກອາໄສ, ຍົກຕົວຢ່າງຕໍ່ກັບກໍາແພງຫີນທີ່ຫັນ ໜ້າ ໄປທາງທິດໃຕ້.
Linnaea parvifolia: Linnaea parvifolia , ຄຳ ສັບຄ້າຍຄື Abelia schumannii , ແມ່ນຊະນິດຂອງຕົ້ນດອກໄມ້ໃນຄອບຄົວ Caprifoliaceae, ທີ່ມີຖິ່ນ ກຳ ເນີດຢູ່ພາກກາງຂອງປະເທດຈີນ. ມັນເປັນໄມ້ພຸ່ມເຄິ່ງຂຽວຕະຫລອດປີສູງເຖິງ 2 ມ (7 ຟຸດ) ໂດຍສູງ 3 ມ (10 ຟຸດ) ກວ້າງ. ດອກກຸຫລາບທີ່ມີກາບດອກສີແດງຖືກຜະລິດໃນລະດູຮ້ອນແລະລະດູໃບໄມ້ປົ່ງ.
tyaihyonii Zabelia: Zabelia tyaihyonii , ຄຳ ສັບຄ້າຍຄື Abelia mosanensis , ທີ່ຮູ້ກັນໃນນາມ abelia ທີ່ມີກິ່ນຫອມ , ແມ່ນຊະນິດຂອງຕົ້ນໄມ້ປ່ຽນໃບໃນຄອບຄົວ Caprifoliaceae honeysuckle. ເຕີບໃຫຍ່ສູງເຖິງ 2 ແມັດແລະກວ້າງ, ມັນແຂງກ່ວາຊະນິດທີ່ກ່ຽວຂ້ອງ, ມີອຸນຫະພູມທີ່ມີຊີວິດລອດຕໍ່າເຖິງ −20 ° C (°4° F). ດອກໄມ້ເປັນຫຼອດເປັນສີຂາວແກມສີບົວແລະມີກິ່ນຫອມສູງ, ປະກົດອອກໃນທ້າຍລະດູໃບໄມ້ປົ່ງ. ໃບສີຂຽວເຫຼື້ອມເປັນສີແດງໃນລະດູໃບໄມ້ປົ່ງກ່ອນທີ່ຈະຕົກ.
Linnaea parvifolia: Linnaea parvifolia , ຄຳ ສັບຄ້າຍຄື Abelia schumannii , ແມ່ນຊະນິດຂອງຕົ້ນດອກໄມ້ໃນຄອບຄົວ Caprifoliaceae, ທີ່ມີຖິ່ນ ກຳ ເນີດຢູ່ພາກກາງຂອງປະເທດຈີນ. ມັນເປັນໄມ້ພຸ່ມເຄິ່ງຂຽວຕະຫລອດປີສູງເຖິງ 2 ມ (7 ຟຸດ) ໂດຍສູງ 3 ມ (10 ຟຸດ) ກວ້າງ. ດອກກຸຫລາບທີ່ມີກາບດອກສີແດງຖືກຜະລິດໃນລະດູຮ້ອນແລະລະດູໃບໄມ້ປົ່ງ.
Linnaea × grandiflora: Linnaea × grandiflora , ຄຳ ສັບຄ້າຍຄື Abelia × grandiflora , ແມ່ນພືດປະສົມຂອງດອກໄມ້ປະສົມໃນຄອບຄົວ honeysuckle Caprifoliaceae, ລ້ຽງໂດຍການປະສົມ L. chinensis ກັບ L. uniflora .
Linnaea × grandiflora: Linnaea × grandiflora , ຄຳ ສັບຄ້າຍຄື Abelia × grandiflora , ແມ່ນພືດປະສົມຂອງດອກໄມ້ປະສົມໃນຄອບຄົວ honeysuckle Caprifoliaceae, ລ້ຽງໂດຍການປະສົມ L. chinensis ກັບ L. uniflora .
Linnaea × grandiflora: Linnaea × grandiflora , ຄຳ ສັບຄ້າຍຄື Abelia × grandiflora , ແມ່ນພືດປະສົມຂອງດອກໄມ້ປະສົມໃນຄອບຄົວ honeysuckle Caprifoliaceae, ລ້ຽງໂດຍການປະສົມ L. chinensis ກັບ L. uniflora .
Abelian: Abelian ອາດຈະອີງໃສ່:
ທິດສະດີທິດສະດີ Abelian ແລະ Tauberian: ໃນວິຊາຄະນິດສາດ, ທິດສະດີທິດສະດີຂອງ Abelian ແລະ Tauberian ແມ່ນທິດສະດີທີ່ໃຫ້ເງື່ອນໄຂ ສຳ ລັບສອງວິທີຂອງການລວມເອົາຊຸດທີ່ແຕກຕ່າງກັນເພື່ອໃຫ້ໄດ້ຜົນດຽວກັນ, ມີຊື່ວ່າ Niels Henrik Abel ແລະ Alfred Tauber. ຕົວຢ່າງຕົ້ນສະບັບແມ່ນທິດສະດີຂອງ Abel ສະແດງໃຫ້ເຫັນວ່າຖ້າຊຸດ ໜຶ່ງ ປ່ຽນໄປໃນຂອບເຂດ ຈຳ ກັດບາງຢ່າງນັ້ນຜົນລວມຂອງ Abel ແມ່ນຂອບເຂດ ຈຳ ກັດດຽວກັນແລະທິດສະດີຂອງ Tauber ສະແດງໃຫ້ເຫັນວ່າຖ້າຜົນບວກຂອງ Abel ມີຕົວຄູນແລະຕົວຄູນມີ ຈຳ ນວນ ໜ້ອຍ ແລ້ວຊຸດດັ່ງກ່າວຈະປ່ຽນເປັນ Abel ຜົນລວມ. ທິດສະດີທິດສະດີທົ່ວໄປຂອງ Abelian ແລະ Tauberian ໃຫ້ຜົນທີ່ຄ້າຍຄືກັນ ສຳ ລັບວິທີການສັງລວມທົ່ວໄປ.
Abelian: Abelian ອາດຈະອີງໃສ່:
Abelian: Abelian ອາດຈະອີງໃສ່:
Abelian 2 ກຸ່ມ: ໃນຄະນິດສາດ, ກຸ່ມ Abelian 2-group ແມ່ນການປຽບທຽບຂະ ໜາດ ທີ່ສູງຂື້ນຂອງກຸ່ມ Abelian, ໃນຄວາມ ໝາຍ ຂອງພຶດຊະຄະນິດທີ່ສູງກວ່າ, ເຊິ່ງໄດ້ຖືກ ນຳ ສະ ເໜີ ໂດຍ Alexander Grothendieck ໃນຂະນະທີ່ສຶກສາໂຄງສ້າງທີ່ບໍ່ມີຕົວຕົນທີ່ຢູ່ອ້ອມຮອບແນວພັນ Abelian ແລະກຸ່ມ Picard. ຍິ່ງໄປກວ່ານັ້ນ, ພວກມັນແມ່ນໃຫ້ໂດຍກຸ່ມກຸ່ມ ເຊິ່ງມີ bifunctor ເປັນ ເຊິ່ງເຮັດ ໜ້າ ທີ່ຢ່າງເປັນທາງການເຊັ່ນ: ກຸ່ມ Abelian. ຄື, the bifunctor ມີແນວຄິດກ່ຽວກັບການປ່ຽນແປງ, ການມີສ່ວນຮ່ວມ, ແລະໂຄງສ້າງຕົວຕົນ. ເຖິງແມ່ນວ່າສິ່ງນີ້ເບິ່ງຄືວ່າເປັນໂຄງສ້າງທີ່ສູງຫຼາຍແລະບໍ່ມີຕົວຕົນ, ແຕ່ມີຕົວຢ່າງຫຼາຍຢ່າງຂອງ Abelian 2-group. ໃນຄວາມເປັນຈິງ, ບາງບ່ອນທີ່ໃຫ້ແບບຕົ້ນແບບ ສຳ ລັບຕົວຢ່າງທີ່ສັບສົນກວ່າເກົ່າຂອງໂຄງສ້າງກ່ຽວກັບພຶດຊະຄະນິດສູງ, ເຊັ່ນວ່າ Abelian n-groups.
ໝວດ ໝູ່ Abelian: ໃນຄະນິດສາດ, ປະເພດ abelian ແມ່ນ ໝວດ ທີ່ຮູບແບບແລະວັດຖຸສາມາດເພີ່ມແລະໃນນັ້ນແກ່ນແລະ cokernels ມີແລະມີຄຸນສົມບັດທີ່ຕ້ອງການ. ຕົວຢ່າງຕົ້ນແບບທີ່ກະຕຸ້ນຂອງປະເພດ abelian ແມ່ນປະເພດຂອງກຸ່ມ abelian, Ab . ທິດສະດີດັ່ງກ່າວໄດ້ເລີ່ມຕົ້ນໃນຄວາມພະຍາຍາມເພື່ອທ້ອນໂຮມທິດສະດີ cohomology ຫຼາຍໆຢ່າງໂດຍ Alexander Grothendieck ແລະເປັນອິດສະຫຼະໃນວຽກງານກ່ອນ ໜ້າ ນີ້ຂອງ David Buchsbaum. ໝວດ ອາເບັນແມ່ນປະເພດທີ່ມີຄວາມ ໝັ້ນ ຄົງ ຫຼາຍ; ຍົກຕົວຢ່າງ, ພວກມັນເປັນປົກກະຕິແລະພວກມັນພໍໃຈກັບງູເຫົ່າ. ຊັ້ນຮຽນຂອງປະເພດ abelian ຖືກປິດພາຍໃຕ້ການກໍ່ສ້າງຫຼາຍປະເພດ, ຍົກຕົວຢ່າງ, ປະເພດຂອງສະລັບສັບຊ້ອນລະບົບຕ່ອງໂສ້ຂອງປະເພດ abelian, ຫຼື ໝວດ ໝູ່ ຂອງອະນຸສອນຈາກປະເພດນ້ອຍໆຈົນເຖິງປະເພດ abelian ແມ່ນ abelian ເຊັ່ນກັນ. ຄຸນລັກສະນະສະຖຽນລະພາບເຫຼົ່ານີ້ເຮັດໃຫ້ພວກເຂົາຫລີກລ້ຽງບໍ່ໄດ້ໃນພຶດຊະຄະນິດ homological ແລະນອກ ເໜືອ ຈາກນັ້ນ; ທິດສະດີມີການ ນຳ ໃຊ້ຫຼັກໃນເລຂາຄະນິດ, ພຶດຊະຄະນິດແລະທິດສະດີປະເພດບໍລິສຸດ. ໝວດ ໝູ່ ຂອງ Abelian ແມ່ນຕັ້ງຊື່ຕາມ Niels Henrik Abel.
ຄວາມແຕກຕ່າງຂອງຊະນິດ ທຳ ອິດ: ໃນຄະນິດສາດ, ຄວາມແຕກຕ່າງຂອງຊະນິດ ທຳ ອິດ ແມ່ນ ຄຳ ສັບພື້ນເມືອງທີ່ໃຊ້ໃນທິດສະດີຂອງ ໜ້າ ດິນ Riemann ແລະເສັ້ນໂຄ້ງ algebraic, ສຳ ລັບຢູ່ທົ່ວທຸກແຫ່ງ - 1 ຄວາມແຕກຕ່າງປົກກະຕິ. ເນື່ອງຈາກ M ແບບສະລັບສັບຊ້ອນ, ຄວາມແຕກຕ່າງຂອງຊະນິດ ທຳ ອິດωແມ່ນສິ່ງດຽວກັນກັບຮູບແບບ 1 ທີ່ມີຢູ່ທົ່ວທຸກແຫ່ງ; ກ່ຽວກັບແນວພັນພຶດຊະຄະນິດ V ທີ່ບໍ່ແມ່ນ ຄຳ ມັນຈະເປັນພາກສ່ວນທົ່ວໂລກຂອງເສັ້ນກາບ sheaf of 1 ຂອງKähler. ບໍ່ວ່າໃນກໍລະນີໃດກໍ່ຕາມ ຄຳ ນິຍາມກໍ່ມີຕົ້ນ ກຳ ເນີດຂອງມັນໃນທິດສະດີຂອງເສດຖີ abelian.
ການຂະຫຍາຍ Abelian: ໃນພຶດຊະຄະນິດທີ່ບໍ່ມີຕົວຕົນ, ການ ຂະຫຍາຍ abelian ແມ່ນການຂະຫຍາຍ Galois ທີ່ກຸ່ມ Galois ແມ່ນ abelian. ໃນເວລາທີ່ກຸ່ມ Galois ກໍ່ແມ່ນວົງຈອນ, ການຂະຫຍາຍຍັງຖືກເອີ້ນວ່າການ ຂະຫຍາຍຮອບວຽນ . ໄປໃນທິດທາງອື່ນ, ການຂະຫຍາຍ Galois ຖືກເອີ້ນວ່າ ແກ້ໄຂໄດ້ ຖ້າກຸ່ມ Galois ຂອງມັນສາມາດແກ້ໄຂໄດ້, ເຊັ່ນ, ຖ້າກຸ່ມດັ່ງກ່າວສາມາດເສີຍຫາຍໄປເປັນຊຸດຂອງການຂະຫຍາຍປົກກະຕິຂອງກຸ່ມ abelian.
ແນວພັນ Abelian: ໃນຄະນິດສາດ, ໂດຍສະເພາະໃນເລຂາຄະນິດພຶຊະຄະນິດ, ວິເຄາະສະລັບສັບຊ້ອນແລະທິດສະດີຈໍານວນພຶຊະຄະນິດ, ເປັນແນວພັນ abelian ເປັນຫຼາຍໆພຶຊະຄະນິດຄາດຄະເນວ່າຍັງເປັນກຸ່ມພຶຊະຄະນິດ, ie, ມີກົດຫມາຍວ່າດ້ວຍກຸ່ມທີ່ສາມາດໄດ້ຮັບການກໍານົດໂດຍປະຕິບັດຫນ້າປົກກະຕິ. ແນວພັນ Abelian ແມ່ນໃນເວລາດຽວກັນໃນບັນດາວັດຖຸທີ່ໄດ້ຮັບການສຶກສາຫຼາຍທີ່ສຸດໃນເລຂາຄະນິດພຶດຊະຄະນິດແລະເຄື່ອງມືທີ່ຂາດບໍ່ໄດ້ ສຳ ລັບການຄົ້ນຄວ້າຫຼາຍກ່ຽວກັບຫົວຂໍ້ອື່ນໆໃນເລຂາຄະນິດພຶດຊະຄະນິດແລະທິດສະດີເລກ.
ກຸ່ມ Abelian: ໃນຄະນິດສາດ, ກຸ່ມອາເບັນ , ເຊິ່ງເອີ້ນວ່າ ກຸ່ມທີ່ເສີຍເມີຍ , ແມ່ນກຸ່ມ ໜຶ່ງ ເຊິ່ງຜົນຂອງການ ນຳ ໃຊ້ການ ດຳ ເນີນງານຂອງກຸ່ມໃຫ້ກັບສອງອົງປະກອບຂອງກຸ່ມບໍ່ຂື້ນກັບລະບຽບທີ່ພວກເຂົາຂຽນ. ນັ້ນແມ່ນ, ການ ດຳ ເນີນງານຂອງກຸ່ມແມ່ນມີຄວາມ ໝາຍ. ນອກ ເໜືອ ຈາກການປະຕິບັດງານ, ຕົວເລກແລະຕົວເລກຕົວຈິງປະກອບເປັນກຸ່ມຊົນເຜົ່າ abelian, ແລະແນວຄິດຂອງກຸ່ມ abelian ອາດຈະຖືກເບິ່ງວ່າເປັນການລວມຕົວຢ່າງຂອງຕົວຢ່າງເຫຼົ່ານີ້. ກຸ່ມ Abelian ແມ່ນມີຊື່ຕາມນັກຄະນິດສາດນັກຮຽນສະຕະວັດທີ 19 Niels Henrik Abel.
ກົນໄກ Higgs: ໃນຮູບແບບມາດຕະຖານຂອງຟີຊິກອະນຸພາກ, ກົນໄກ Higgs ແມ່ນມີຄວາມ ຈຳ ເປັນໃນການອະທິບາຍກົນໄກການຜະລິດຂອງຊັບສິນ" ມວນສານ" ສຳ ລັບໂບດວັດ. ຖ້າບໍ່ມີກົນໄກ Higgs, bosons ທັງ ໝົດ (ໜຶ່ງ ໃນສອງຊັ້ນຂອງອະນຸພາກ, ສ່ວນອື່ນໆທີ່ເປັນ fermions) ຈະຖືກພິຈາລະນາເປັນ ຈຳ ນວນມະຫາສານ, ແຕ່ວ່າການວັດແທກສະແດງໃຫ້ເຫັນວ່າ ໂບດ W + , W - , ແລະ Z 0 ຕົວຈິງມີມະຫາຊົນຂ້ອນຂ້າງໃຫຍ່ປະມານ 80 GeV / c 2 . ພາກສະຫນາມ Higgs ແກ້ໄຂບັນຫານີ້. ຄໍາອະທິບາຍທີ່ລຽບງ່າຍທີ່ສຸດຂອງກົນໄກເພີ່ມສະ ໜາມ quantum (ພາກສະ ໜາມ Higgs) ທີ່ແຜ່ລາມໄປເຖິງພື້ນທີ່ທັງ ໝົດ ຂອງ Model Model. ຂ້າງລຸ່ມນີ້ອຸນຫະພູມທີ່ສູງທີ່ສຸດບາງ, ພາກສະຫນາມເຮັດໃຫ້ເກີດການແຍກ symmetry spontaneous ໃນລະຫວ່າງການໂຕ້ຕອບ. ການແຕກແຍກຂອງ symmetry ກະຕຸ້ນກົນໄກ Higgs, ເຮັດໃຫ້ bosons ທີ່ມັນພົວພັນກັບມີມະຫາຊົນ. ໃນຮູບແບບມາດຕະຖານ, ປະໂຫຍກທີ່ວ່າ "ກົນໄກ Higgs" ໝາຍ ເຖິງໂດຍສະເພາະການຜະລິດຂອງມວນສານ ສຳ ລັບ W ± , ແລະ Z ວັດວັດທີ່ອ່ອນເພຍໂດຍຜ່ານສາຍແຍກໄຟຟ້າທີ່ມີໄຟຟ້າເອເລັກໂຕຣນິກ. The Heavy Hadron Collider ທີ່ CERN ປະກາດຜົນໄດ້ຮັບທີ່ສອດຄ້ອງກັບອະນຸພາກ Higgs ໃນວັນທີ 14 ມີນາ 2013, ເຮັດໃຫ້ມັນມີຄວາມເປັນໄປໄດ້ສູງທີ່ສຸດວ່າພາກສະ ໜາມ ຫລືຄ້າຍຄືມັນມີຢູ່ແລະອະທິບາຍວ່າກົນໄກ Higgs ເກີດຂື້ນໃນ ທຳ ມະຊາດແນວໃດ.
ກົນໄກ Higgs: ໃນຮູບແບບມາດຕະຖານຂອງຟີຊິກອະນຸພາກ, ກົນໄກ Higgs ແມ່ນມີຄວາມ ຈຳ ເປັນໃນການອະທິບາຍກົນໄກການຜະລິດຂອງຊັບສິນ" ມວນສານ" ສຳ ລັບໂບດວັດ. ຖ້າບໍ່ມີກົນໄກ Higgs, bosons ທັງ ໝົດ (ໜຶ່ງ ໃນສອງຊັ້ນຂອງອະນຸພາກ, ສ່ວນອື່ນໆທີ່ເປັນ fermions) ຈະຖືກພິຈາລະນາເປັນ ຈຳ ນວນມະຫາສານ, ແຕ່ວ່າການວັດແທກສະແດງໃຫ້ເຫັນວ່າ ໂບດ W + , W - , ແລະ Z 0 ຕົວຈິງມີມະຫາຊົນຂ້ອນຂ້າງໃຫຍ່ປະມານ 80 GeV / c 2 . ພາກສະຫນາມ Higgs ແກ້ໄຂບັນຫານີ້. ຄໍາອະທິບາຍທີ່ລຽບງ່າຍທີ່ສຸດຂອງກົນໄກເພີ່ມສະ ໜາມ quantum (ພາກສະ ໜາມ Higgs) ທີ່ແຜ່ລາມໄປເຖິງພື້ນທີ່ທັງ ໝົດ ຂອງ Model Model. ຂ້າງລຸ່ມນີ້ອຸນຫະພູມທີ່ສູງທີ່ສຸດບາງ, ພາກສະຫນາມເຮັດໃຫ້ເກີດການແຍກ symmetry spontaneous ໃນລະຫວ່າງການໂຕ້ຕອບ. ການແຕກແຍກຂອງ symmetry ກະຕຸ້ນກົນໄກ Higgs, ເຮັດໃຫ້ bosons ທີ່ມັນພົວພັນກັບມີມະຫາຊົນ. ໃນຮູບແບບມາດຕະຖານ, ປະໂຫຍກທີ່ວ່າ "ກົນໄກ Higgs" ໝາຍ ເຖິງໂດຍສະເພາະການຜະລິດຂອງມວນສານ ສຳ ລັບ W ± , ແລະ Z ວັດວັດທີ່ອ່ອນເພຍໂດຍຜ່ານສາຍແຍກໄຟຟ້າທີ່ມີໄຟຟ້າເອເລັກໂຕຣນິກ. The Heavy Hadron Collider ທີ່ CERN ປະກາດຜົນໄດ້ຮັບທີ່ສອດຄ້ອງກັບອະນຸພາກ Higgs ໃນວັນທີ 14 ມີນາ 2013, ເຮັດໃຫ້ມັນມີຄວາມເປັນໄປໄດ້ສູງທີ່ສຸດວ່າພາກສະ ໜາມ ຫລືຄ້າຍຄືມັນມີຢູ່ແລະອະທິບາຍວ່າກົນໄກ Higgs ເກີດຂື້ນໃນ ທຳ ມະຊາດແນວໃດ.
ສ່ວນປະກອບຂອງ Abelian: ໃນຄະນິດສາດ, ການ ປະສົມປະສານ abelian , ຊື່ຕາມນັກວິຊາຄະນິດສາດນໍເວ Niels Henrik Abel, ແມ່ນສ່ວນປະກອບໃນຍົນທີ່ສັບຊ້ອນຂອງແບບຟອມ
ຕົວແປພຶດຊະຄະນິດ: ໃນຄະນິດສາດ, ຕົວແປພາສາ Lie ແມ່ນຊ່ອງ vector ຮ່ວມກັນກັບການປະຕິບັດງານທີ່ເອີ້ນວ່າ Lie bracket , ເປັນແຜນທີ່ bilinear ສຳ ຮອງ , ທີ່ພໍໃຈກັບຕົວຕົນຂອງ Jacobi. ພື້ນທີ່ vector ພ້ອມກັນກັບການປະຕິບັດງານນີ້ແມ່ນຄະນິດສາດທີ່ບໍ່ເຂົ້າກັນ, ໝາຍ ຄວາມວ່າວົງເລັບ Lie ບໍ່ ຈຳ ເປັນຕ້ອງມີສ່ວນຮ່ວມ.
ກຸ່ມ Abelian Lie: ໃນເລຂາຄະນິດ, ກຸ່ມຕົວະ Abelian ແມ່ນກຸ່ມ Lie ທີ່ແມ່ນກຸ່ມ abelian.
ເອກະສານອ້າງອີງ Abel: Polynomials Abel ໃນຄະນິດສາດປະກອບເປັນໄລຍະ polynomial, ໄລຍະທີ n ແມ່ນຂອງຮູບແບບ
ທິດສະດີທິດສະດີ Abelian ແລະ Tauberian: ໃນວິຊາຄະນິດສາດ, ທິດສະດີທິດສະດີຂອງ Abelian ແລະ Tauberian ແມ່ນທິດສະດີທີ່ໃຫ້ເງື່ອນໄຂ ສຳ ລັບສອງວິທີຂອງການລວມເອົາຊຸດທີ່ແຕກຕ່າງກັນເພື່ອໃຫ້ໄດ້ຜົນດຽວກັນ, ມີຊື່ວ່າ Niels Henrik Abel ແລະ Alfred Tauber. ຕົວຢ່າງຕົ້ນສະບັບແມ່ນທິດສະດີຂອງ Abel ສະແດງໃຫ້ເຫັນວ່າຖ້າຊຸດ ໜຶ່ງ ປ່ຽນໄປໃນຂອບເຂດ ຈຳ ກັດບາງຢ່າງນັ້ນຜົນລວມຂອງ Abel ແມ່ນຂອບເຂດ ຈຳ ກັດດຽວກັນແລະທິດສະດີຂອງ Tauber ສະແດງໃຫ້ເຫັນວ່າຖ້າຜົນບວກຂອງ Abel ມີຕົວຄູນແລະຕົວຄູນມີ ຈຳ ນວນ ໜ້ອຍ ແລ້ວຊຸດດັ່ງກ່າວຈະປ່ຽນເປັນ Abel ຜົນລວມ. ທິດສະດີທິດສະດີທົ່ວໄປຂອງ Abelian ແລະ Tauberian ໃຫ້ຜົນທີ່ຄ້າຍຄືກັນ ສຳ ລັບວິທີການສັງລວມທົ່ວໄປ.
ແນວພັນ Abelian: ໃນຄະນິດສາດ, ໂດຍສະເພາະໃນເລຂາຄະນິດພຶຊະຄະນິດ, ວິເຄາະສະລັບສັບຊ້ອນແລະທິດສະດີຈໍານວນພຶຊະຄະນິດ, ເປັນແນວພັນ abelian ເປັນຫຼາຍໆພຶຊະຄະນິດຄາດຄະເນວ່າຍັງເປັນກຸ່ມພຶຊະຄະນິດ, ie, ມີກົດຫມາຍວ່າດ້ວຍກຸ່ມທີ່ສາມາດໄດ້ຮັບການກໍານົດໂດຍປະຕິບັດຫນ້າປົກກະຕິ. ແນວພັນ Abelian ແມ່ນໃນເວລາດຽວກັນໃນບັນດາວັດຖຸທີ່ໄດ້ຮັບການສຶກສາຫຼາຍທີ່ສຸດໃນເລຂາຄະນິດພຶດຊະຄະນິດແລະເຄື່ອງມືທີ່ຂາດບໍ່ໄດ້ ສຳ ລັບການຄົ້ນຄວ້າຫຼາຍກ່ຽວກັບຫົວຂໍ້ອື່ນໆໃນເລຂາຄະນິດພຶດຊະຄະນິດແລະທິດສະດີເລກ.
ຄະນິດສາດກ່ຽວຂ້ອງ: ໃນຄະນິດສາດ, ພຶດຊະ ຄະນິດກ່ຽວຂ້ອງ ແມ່ນໂຄງສ້າງກ່ຽວກັບພຶດຊະຄະນິດທີ່ມີການປະຕິບັດການທີ່ ເໝາະ ສົມຂອງການເພີ່ມ, ການຄູນ, ແລະການຄູນ scalar ໂດຍອົງປະກອບໃນບາງຂະ ແໜງ ນອກຈາກນັ້ນແລະຫຼາຍປະຕິບັດງານຮ່ວມກັນໃຫ້ໂຄງປະກອບການວົງໄດ້; ນອກຈາກນັ້ນແລະ scalar ການດໍາເນີນງານຫຼາຍຮ່ວມກັນໃຫ້ໂຄງປະກອບການຂອງຊ່ອງ vector ໃນໄລຍະ K ໄດ້. ໃນບົດຄວາມນີ້ພວກເຮົາຍັງຈະໃຊ້ ຄຳ ວ່າ K -algebra ເພື່ອ ໝາຍ ເຖິງພຶດຊະຄະນິດທີ່ກ່ຽວຂ້ອງກັບສະ ໜາມ K. ຕົວຢ່າງ ທຳ ອິດຂອງມາດຕະຖານ K -algebra ແມ່ນແຫວນຂອງ matrices ສີ່ຫລ່ຽມໃນໄລຍະ K , ດ້ວຍການຄູນຕາຕະລາງປົກກະຕິ.
ທິດສະດີທິດສະດີ Abelian ແລະ Tauberian: ໃນວິຊາຄະນິດສາດ, ທິດສະດີທິດສະດີຂອງ Abelian ແລະ Tauberian ແມ່ນທິດສະດີທີ່ໃຫ້ເງື່ອນໄຂ ສຳ ລັບສອງວິທີຂອງການລວມເອົາຊຸດທີ່ແຕກຕ່າງກັນເພື່ອໃຫ້ໄດ້ຜົນດຽວກັນ, ມີຊື່ວ່າ Niels Henrik Abel ແລະ Alfred Tauber. ຕົວຢ່າງຕົ້ນສະບັບແມ່ນທິດສະດີຂອງ Abel ສະແດງໃຫ້ເຫັນວ່າຖ້າຊຸດ ໜຶ່ງ ປ່ຽນໄປໃນຂອບເຂດ ຈຳ ກັດບາງຢ່າງນັ້ນຜົນລວມຂອງ Abel ແມ່ນຂອບເຂດ ຈຳ ກັດດຽວກັນແລະທິດສະດີຂອງ Tauber ສະແດງໃຫ້ເຫັນວ່າຖ້າຜົນບວກຂອງ Abel ມີຕົວຄູນແລະຕົວຄູນມີ ຈຳ ນວນ ໜ້ອຍ ແລ້ວຊຸດດັ່ງກ່າວຈະປ່ຽນເປັນ Abel ຜົນລວມ. ທິດສະດີທິດສະດີທົ່ວໄປຂອງ Abelian ແລະ Tauberian ໃຫ້ຜົນທີ່ຄ້າຍຄືກັນ ສຳ ລັບວິທີການສັງລວມທົ່ວໄປ.
ທິດສະດີທິດສະດີ Abelian ແລະ Tauberian: ໃນວິຊາຄະນິດສາດ, ທິດສະດີທິດສະດີຂອງ Abelian ແລະ Tauberian ແມ່ນທິດສະດີທີ່ໃຫ້ເງື່ອນໄຂ ສຳ ລັບສອງວິທີຂອງການລວມເອົາຊຸດທີ່ແຕກຕ່າງກັນເພື່ອໃຫ້ໄດ້ຜົນດຽວກັນ, ມີຊື່ວ່າ Niels Henrik Abel ແລະ Alfred Tauber. ຕົວຢ່າງຕົ້ນສະບັບແມ່ນທິດສະດີຂອງ Abel ສະແດງໃຫ້ເຫັນວ່າຖ້າຊຸດ ໜຶ່ງ ປ່ຽນໄປໃນຂອບເຂດ ຈຳ ກັດບາງຢ່າງນັ້ນຜົນລວມຂອງ Abel ແມ່ນຂອບເຂດ ຈຳ ກັດດຽວກັນແລະທິດສະດີຂອງ Tauber ສະແດງໃຫ້ເຫັນວ່າຖ້າຜົນບວກຂອງ Abel ມີຕົວຄູນແລະຕົວຄູນມີ ຈຳ ນວນ ໜ້ອຍ ແລ້ວຊຸດດັ່ງກ່າວຈະປ່ຽນເປັນ Abel ຜົນລວມ. ທິດສະດີທິດສະດີທົ່ວໄປຂອງ Abelian ແລະ Tauberian ໃຫ້ຜົນທີ່ຄ້າຍຄືກັນ ສຳ ລັບວິທີການສັງລວມທົ່ວໄປ.
ໝວດ ໝູ່ Abelian: ໃນຄະນິດສາດ, ປະເພດ abelian ແມ່ນ ໝວດ ທີ່ຮູບແບບແລະວັດຖຸສາມາດເພີ່ມແລະໃນນັ້ນແກ່ນແລະ cokernels ມີແລະມີຄຸນສົມບັດທີ່ຕ້ອງການ. ຕົວຢ່າງຕົ້ນແບບທີ່ກະຕຸ້ນຂອງປະເພດ abelian ແມ່ນປະເພດຂອງກຸ່ມ abelian, Ab . ທິດສະດີດັ່ງກ່າວໄດ້ເລີ່ມຕົ້ນໃນຄວາມພະຍາຍາມເພື່ອທ້ອນໂຮມທິດສະດີ cohomology ຫຼາຍໆຢ່າງໂດຍ Alexander Grothendieck ແລະເປັນອິດສະຫຼະໃນວຽກງານກ່ອນ ໜ້າ ນີ້ຂອງ David Buchsbaum. ໝວດ ອາເບັນແມ່ນປະເພດທີ່ມີຄວາມ ໝັ້ນ ຄົງ ຫຼາຍ; ຍົກຕົວຢ່າງ, ພວກມັນເປັນປົກກະຕິແລະພວກມັນພໍໃຈກັບງູເຫົ່າ. ຊັ້ນຮຽນຂອງປະເພດ abelian ຖືກປິດພາຍໃຕ້ການກໍ່ສ້າງຫຼາຍປະເພດ, ຍົກຕົວຢ່າງ, ປະເພດຂອງສະລັບສັບຊ້ອນລະບົບຕ່ອງໂສ້ຂອງປະເພດ abelian, ຫຼື ໝວດ ໝູ່ ຂອງອະນຸສອນຈາກປະເພດນ້ອຍໆຈົນເຖິງປະເພດ abelian ແມ່ນ abelian ເຊັ່ນກັນ. ຄຸນລັກສະນະສະຖຽນລະພາບເຫຼົ່ານີ້ເຮັດໃຫ້ພວກເຂົາຫລີກລ້ຽງບໍ່ໄດ້ໃນພຶດຊະຄະນິດ homological ແລະນອກ ເໜືອ ຈາກນັ້ນ; ທິດສະດີມີການ ນຳ ໃຊ້ຫຼັກໃນເລຂາຄະນິດ, ພຶດຊະຄະນິດແລະທິດສະດີປະເພດບໍລິສຸດ. ໝວດ ໝູ່ ຂອງ Abelian ແມ່ນຕັ້ງຊື່ຕາມ Niels Henrik Abel.
ໝວດ ໝູ່ Abelian: ໃນຄະນິດສາດ, ປະເພດ abelian ແມ່ນ ໝວດ ທີ່ຮູບແບບແລະວັດຖຸສາມາດເພີ່ມແລະໃນນັ້ນແກ່ນແລະ cokernels ມີແລະມີຄຸນສົມບັດທີ່ຕ້ອງການ. ຕົວຢ່າງຕົ້ນແບບທີ່ກະຕຸ້ນຂອງປະເພດ abelian ແມ່ນປະເພດຂອງກຸ່ມ abelian, Ab . ທິດສະດີດັ່ງກ່າວໄດ້ເລີ່ມຕົ້ນໃນຄວາມພະຍາຍາມເພື່ອທ້ອນໂຮມທິດສະດີ cohomology ຫຼາຍໆຢ່າງໂດຍ Alexander Grothendieck ແລະເປັນອິດສະຫຼະໃນວຽກງານກ່ອນ ໜ້າ ນີ້ຂອງ David Buchsbaum. ໝວດ ອາເບັນແມ່ນປະເພດທີ່ມີຄວາມ ໝັ້ນ ຄົງ ຫຼາຍ; ຍົກຕົວຢ່າງ, ພວກມັນເປັນປົກກະຕິແລະພວກມັນພໍໃຈກັບງູເຫົ່າ. ຊັ້ນຮຽນຂອງປະເພດ abelian ຖືກປິດພາຍໃຕ້ການກໍ່ສ້າງຫຼາຍປະເພດ, ຍົກຕົວຢ່າງ, ປະເພດຂອງສະລັບສັບຊ້ອນລະບົບຕ່ອງໂສ້ຂອງປະເພດ abelian, ຫຼື ໝວດ ໝູ່ ຂອງອະນຸສອນຈາກປະເພດນ້ອຍໆຈົນເຖິງປະເພດ abelian ແມ່ນ abelian ເຊັ່ນກັນ. ຄຸນລັກສະນະສະຖຽນລະພາບເຫຼົ່ານີ້ເຮັດໃຫ້ພວກເຂົາຫລີກລ້ຽງບໍ່ໄດ້ໃນພຶດຊະຄະນິດ homological ແລະນອກ ເໜືອ ຈາກນັ້ນ; ທິດສະດີມີການ ນຳ ໃຊ້ຫຼັກໃນເລຂາຄະນິດ, ພຶດຊະຄະນິດແລະທິດສະດີປະເພດບໍລິສຸດ. ໝວດ ໝູ່ ຂອງ Abelian ແມ່ນຕັ້ງຊື່ຕາມ Niels Henrik Abel.
ຟັງຊັນຄວາມສັບສົນ: ໃນວິທະຍາສາດຄອມພິວເຕີ້, ໜ້າ ທີ່ ສັບສົນ ຂອງສະຕິງ, ລຳ ດັບທີ່ຈົບງາມຫລືເປັນນິດຂອງຕົວອັກສອນຈາກຕົວ ໜັງ ສືບາງຕົວ, ແມ່ນ ໜ້າ ທີ່ທີ່ນັບ ຈຳ ນວນປັດໃຈທີ່ແຕກຕ່າງຈາກສະຕິງນັ້ນ. ໂດຍທົ່ວໄປແລ້ວ, ໜ້າ ທີ່ສັບສົນຂອງພາສາ ໜຶ່ງ, ຊຸດຂອງ ຄຳ ທີ່ມີລະດັບສະຫງ່າງາມ ເໜືອ ໜັງ ສື, ນັບ ຈຳ ນວນ ຄຳ ສັບທີ່ແຕກຕ່າງຂອງຄວາມຍາວທີ່ໃຫ້.
ກຸ່ມທີ່ຄອບຄຸມ: ໃນຄະນິດສາດ, ກຸ່ມຄອບຄຸມຂອງກຸ່ມ H topological ເປັນພື້ນທີ່ຄອບຄຸມ G ຂອງ H ເຊັ່ນວ່າ G ເປັນກຸ່ມ topological ແລະແຜນທີ່ທີ່ຄອບຄຸມ p: G → H ເປັນ homomorphism ກຸ່ມຢ່າງຕໍ່ເນື່ອງ. ແຜນທີ່ p ເອີ້ນວ່າການ ປົກຫຸ້ມຂອງ homomorphism . ກໍລະນີທີ່ເກີດຂື້ນເລື້ອຍໆແມ່ນ ກຸ່ມປົກຫຸ້ມຄູ່ , ໜ້າ ປົກດ້ານສອງດ້ານທີ່ດ້ານເທິງເຊິ່ງ H ມີດັດຊະນີ 2 ໃນ G ; ຕົວຢ່າງລວມມີກຸ່ມ ໝຸນ, ກຸ່ມເຂັມ, ແລະກຸ່ມສົນທະນາ.
ຄວາມແຕກຕ່າງຂອງຊະນິດ ທຳ ອິດ: ໃນຄະນິດສາດ, ຄວາມແຕກຕ່າງຂອງຊະນິດ ທຳ ອິດ ແມ່ນ ຄຳ ສັບພື້ນເມືອງທີ່ໃຊ້ໃນທິດສະດີຂອງ ໜ້າ ດິນ Riemann ແລະເສັ້ນໂຄ້ງ algebraic, ສຳ ລັບຢູ່ທົ່ວທຸກແຫ່ງ - 1 ຄວາມແຕກຕ່າງປົກກະຕິ. ເນື່ອງຈາກ M ແບບສະລັບສັບຊ້ອນ, ຄວາມແຕກຕ່າງຂອງຊະນິດ ທຳ ອິດωແມ່ນສິ່ງດຽວກັນກັບຮູບແບບ 1 ທີ່ມີຢູ່ທົ່ວທຸກແຫ່ງ; ກ່ຽວກັບແນວພັນພຶດຊະຄະນິດ V ທີ່ບໍ່ແມ່ນ ຄຳ ມັນຈະເປັນພາກສ່ວນທົ່ວໂລກຂອງເສັ້ນກາບ sheaf of 1 ຂອງKähler. ບໍ່ວ່າໃນກໍລະນີໃດກໍ່ຕາມ ຄຳ ນິຍາມກໍ່ມີຕົ້ນ ກຳ ເນີດຂອງມັນໃນທິດສະດີຂອງເສດຖີ abelian.
ການຂະຫຍາຍ Abelian: ໃນພຶດຊະຄະນິດທີ່ບໍ່ມີຕົວຕົນ, ການ ຂະຫຍາຍ abelian ແມ່ນການຂະຫຍາຍ Galois ທີ່ກຸ່ມ Galois ແມ່ນ abelian. ໃນເວລາທີ່ກຸ່ມ Galois ກໍ່ແມ່ນວົງຈອນ, ການຂະຫຍາຍຍັງຖືກເອີ້ນວ່າການ ຂະຫຍາຍຮອບວຽນ . ໄປໃນທິດທາງອື່ນ, ການຂະຫຍາຍ Galois ຖືກເອີ້ນວ່າ ແກ້ໄຂໄດ້ ຖ້າກຸ່ມ Galois ຂອງມັນສາມາດແກ້ໄຂໄດ້, ເຊັ່ນ, ຖ້າກຸ່ມດັ່ງກ່າວສາມາດເສີຍຫາຍໄປເປັນຊຸດຂອງການຂະຫຍາຍປົກກະຕິຂອງກຸ່ມ abelian.
ການຂະຫຍາຍ Abelian: ໃນພຶດຊະຄະນິດທີ່ບໍ່ມີຕົວຕົນ, ການ ຂະຫຍາຍ abelian ແມ່ນການຂະຫຍາຍ Galois ທີ່ກຸ່ມ Galois ແມ່ນ abelian. ໃນເວລາທີ່ກຸ່ມ Galois ກໍ່ແມ່ນວົງຈອນ, ການຂະຫຍາຍຍັງຖືກເອີ້ນວ່າການ ຂະຫຍາຍຮອບວຽນ . ໄປໃນທິດທາງອື່ນ, ການຂະຫຍາຍ Galois ຖືກເອີ້ນວ່າ ແກ້ໄຂໄດ້ ຖ້າກຸ່ມ Galois ຂອງມັນສາມາດແກ້ໄຂໄດ້, ເຊັ່ນ, ຖ້າກຸ່ມດັ່ງກ່າວສາມາດເສີຍຫາຍໄປເປັນຊຸດຂອງການຂະຫຍາຍປົກກະຕິຂອງກຸ່ມ abelian.
ແນວພັນ Abelian: ໃນຄະນິດສາດ, ໂດຍສະເພາະໃນເລຂາຄະນິດພຶຊະຄະນິດ, ວິເຄາະສະລັບສັບຊ້ອນແລະທິດສະດີຈໍານວນພຶຊະຄະນິດ, ເປັນແນວພັນ abelian ເປັນຫຼາຍໆພຶຊະຄະນິດຄາດຄະເນວ່າຍັງເປັນກຸ່ມພຶຊະຄະນິດ, ie, ມີກົດຫມາຍວ່າດ້ວຍກຸ່ມທີ່ສາມາດໄດ້ຮັບການກໍານົດໂດຍປະຕິບັດຫນ້າປົກກະຕິ. ແນວພັນ Abelian ແມ່ນໃນເວລາດຽວກັນໃນບັນດາວັດຖຸທີ່ໄດ້ຮັບການສຶກສາຫຼາຍທີ່ສຸດໃນເລຂາຄະນິດພຶດຊະຄະນິດແລະເຄື່ອງມືທີ່ຂາດບໍ່ໄດ້ ສຳ ລັບການຄົ້ນຄວ້າຫຼາຍກ່ຽວກັບຫົວຂໍ້ອື່ນໆໃນເລຂາຄະນິດພຶດຊະຄະນິດແລະທິດສະດີເລກ.
ທິດສະດີ Gauge: ໃນດ້ານຟີຊິກ, ທິດສະດີການວັດແທກ ແມ່ນປະເພດຂອງທິດສະດີພາກສະ ໜາມ ເຊິ່ງ Lagrangian ບໍ່ປ່ຽນແປງພາຍໃຕ້ການປ່ຽນແປງຂອງທ້ອງຖິ່ນຈາກກຸ່ມ Lie.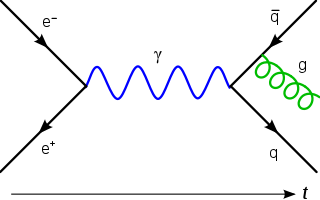
ຕະຫລົກທາງຄະນິດສາດ: ຕະຫລົກທາງຄະນິດສາດ ແມ່ນຮູບແບບຂອງການຕະຫລົກທີ່ເພິ່ງພາແງ່ມຸມດ້ານຂອງຄະນິດສາດຫລືຕົວຢ່າງຂອງນັກຄະນິດສາດ. ຄວາມຕະຫລົກອາດຈະມາຈາກ pun, ຫລືຈາກຄວາມ ໝາຍ ສອງເທົ່າຂອງ ຄຳ ສັບທາງຄະນິດສາດ, ຫລືມາຈາກຄວາມເຂົ້າໃຈຜິດຂອງຄົນທີ່ຄິດກ່ຽວກັບແນວຄິດທາງຄະນິດສາດ. ນັກຄະນິດສາດແລະນັກຂຽນ John Allen Paulos ໃນປື້ມ ຄະນິດສາດແລະ Humor ຂອງລາວໄດ້ ອະທິບາຍຫລາຍວິທີທາງຄະນິດສາດ, ໂດຍທົ່ວໄປຖືວ່າກິດຈະ ກຳ ທີ່ແຫ້ງ, ເປັນທາງການ, ຊ້ ຳ ກັບການຕະຫລົກ, ກິດຈະ ກຳ ທີ່ວ່າງແລະບໍ່ສອດຄ່ອງ: ທັງສອງຮູບແບບຂອງ "ການຫຼີ້ນປັນຍາ"; ທັງສອງມີ "ເຫດຜົນ, ຮູບແບບ, ກົດລະບຽບ, ໂຄງສ້າງ"; ແລະທັງສອງແມ່ນ "ເສດຖະກິດແລະຊັດເຈນ".
ກຸ່ມ Abelian: ໃນຄະນິດສາດ, ກຸ່ມອາເບັນ , ເຊິ່ງເອີ້ນວ່າ ກຸ່ມທີ່ເສີຍເມີຍ , ແມ່ນກຸ່ມ ໜຶ່ງ ເຊິ່ງຜົນຂອງການ ນຳ ໃຊ້ການ ດຳ ເນີນງານຂອງກຸ່ມໃຫ້ກັບສອງອົງປະກອບຂອງກຸ່ມບໍ່ຂື້ນກັບລະບຽບທີ່ພວກເຂົາຂຽນ. ນັ້ນແມ່ນ, ການ ດຳ ເນີນງານຂອງກຸ່ມແມ່ນມີຄວາມ ໝາຍ. ນອກ ເໜືອ ຈາກການປະຕິບັດງານ, ຕົວເລກແລະຕົວເລກຕົວຈິງປະກອບເປັນກຸ່ມຊົນເຜົ່າ abelian, ແລະແນວຄິດຂອງກຸ່ມ abelian ອາດຈະຖືກເບິ່ງວ່າເປັນການລວມຕົວຢ່າງຂອງຕົວຢ່າງເຫຼົ່ານີ້. ກຸ່ມ Abelian ແມ່ນມີຊື່ຕາມນັກຄະນິດສາດນັກຮຽນສະຕະວັດທີ 19 Niels Henrik Abel.
ກຸ່ມ Abelian: ໃນຄະນິດສາດ, ກຸ່ມອາເບັນ , ເຊິ່ງເອີ້ນວ່າ ກຸ່ມທີ່ເສີຍເມີຍ , ແມ່ນກຸ່ມ ໜຶ່ງ ເຊິ່ງຜົນຂອງການ ນຳ ໃຊ້ການ ດຳ ເນີນງານຂອງກຸ່ມໃຫ້ກັບສອງອົງປະກອບຂອງກຸ່ມບໍ່ຂື້ນກັບລະບຽບທີ່ພວກເຂົາຂຽນ. ນັ້ນແມ່ນ, ການ ດຳ ເນີນງານຂອງກຸ່ມແມ່ນມີຄວາມ ໝາຍ. ນອກ ເໜືອ ຈາກການປະຕິບັດງານ, ຕົວເລກແລະຕົວເລກຕົວຈິງປະກອບເປັນກຸ່ມຊົນເຜົ່າ abelian, ແລະແນວຄິດຂອງກຸ່ມ abelian ອາດຈະຖືກເບິ່ງວ່າເປັນການລວມຕົວຢ່າງຂອງຕົວຢ່າງເຫຼົ່ານີ້. ກຸ່ມ Abelian ແມ່ນມີຊື່ຕາມນັກຄະນິດສາດນັກຮຽນສະຕະວັດທີ 19 Niels Henrik Abel.
ສ່ວນປະກອບຂອງ Abelian: ໃນຄະນິດສາດ, ການ ປະສົມປະສານ abelian , ຊື່ຕາມນັກວິຊາຄະນິດສາດນໍເວ Niels Henrik Abel, ແມ່ນສ່ວນປະກອບໃນຍົນທີ່ສັບຊ້ອນຂອງແບບຟອມ
ສູດທ້ອງຖິ່ນ ສຳ ລັບ cohomology ເທົ່າທຽມກັນ: ໃນຮູບເລຂາຄະນິດຄວາມແຕກຕ່າງ, ສູດການແປພາສາທ້ອງຖິ່ນລະ ບຸວ່າ: ສຳ ລັບຮູບແບບຄວາມແຕກຕ່າງ equivariant ທີ່ປິດຢ່າງສະ ໝໍ່າ ສະ ເໝີ ກ່ຽວກັບ orbifold M ທີ່ມີການປະຕິບັດ torus ແລະສໍາລັບຂະຫນາດນ້ອຍພຽງພໍ ໃນພຶດຊະຄະນິດ Lie of the torus T ,
ຊຸດ Divergent: ໃນຄະນິດສາດ, ຊຸດທີ່ແຕກຕ່າງກັນ ແມ່ນ ຊຸດທີ່ ບໍ່ມີຂອບເຂດເຊິ່ງບໍ່ແມ່ນການປ່ຽນແປງ, ໝາຍ ຄວາມວ່າ ລຳ ດັບທີ່ບໍ່ມີຂອບເຂດຂອງ ຈຳ ນວນສ່ວນ ໜຶ່ງ ຂອງຊຸດບໍ່ມີຂອບເຂດ ຈຳ ກັດ.
Monoid: ໃນພຶດຊະຄະນິດທີ່ບໍ່ມີຕົວຕົນ, ສາຂາຂອງຄະນິດສາດ, monoid ແມ່ນຊຸດທີ່ຕິດຕັ້ງດ້ວຍລະບົບຖານສອງທີ່ກ່ຽວຂ້ອງແລະອົງປະກອບຕົວຕົນ.
ທິດສະດີໃນຊັ້ນຮຽນ: ໃນດ້ານຄະນິດສາດ, ທິດສະດີພາກສະ ໜາມ ຫ້ອງຮຽນ ແມ່ນສາຂາຂອງທິດສະດີຄະນິດສາດທີ່ກ່ຽວຂ້ອງກັບການຂະຫຍາຍ abelian ຂອງຂົງເຂດ ໝາຍ ເລກ, ຂົງເຂດທົ່ວໂລກມີລັກສະນະບວກ, ແລະຂົງເຂດທ້ອງຖິ່ນ. ທິດສະດີດັ່ງກ່າວມີຕົ້ນ ກຳ ເນີດມາໃນຫຼັກຖານສະແດງການຕອບແທນສີ່ຫລ່ຽມໂດຍ Gauss ໃນທ້າຍສະຕະວັດທີ 18. ແນວຄວາມຄິດເຫຼົ່ານີ້ໄດ້ຖືກພັດທະນາໃນສັດຕະວັດຕໍ່ໄປ, ເຊິ່ງກໍ່ໃຫ້ເກີດການໂຕ້ຖຽງຂອງ Hilbert ເຊິ່ງໄດ້ຖືກພິສູດໂດຍຕໍ່ມາໂດຍ Takagi ແລະ Artin. ການພິສູດແລະຫຼັກຖານສະແດງເຫຼົ່ານີ້ປະກອບເປັນຮ່າງກາຍຫຼັກຂອງທິດສະດີພາກສະ ໜາມ.
Idempotent (ທິດສະດີວົງແຫວນ): ໃນທິດສະດີວົງເປັນອົງປະກອບ idempotent ຫລືພຽງແຕ່ເປັນ idempotent, ຂອງວົງແມ່ນເປັນອົງປະກອບດັ່ງກ່າວວ່າ 2 = a. ນັ້ນແມ່ນ, ອົງປະກອບແມ່ນ idempotent ພາຍໃຕ້ການຄູນຂອງວົງ. ໂດຍບໍ່ສົນໃຈຫຼັງຈາກນັ້ນ, ທ່ານຍັງສາມາດສະຫຼຸບໄດ້ວ່າ a = a 2 = a 3 = a 4 = ... = a n ສຳ ລັບຕົວເລກບວກບວກ n . ຍົກຕົວຢ່າງ, ອົງປະກອບທີ່ບໍ່ ສຳ ຄັນຂອງວົງແຫວນມາຕຣິກເບື້ອງແມ່ນທີ່ແນ່ນອນວ່າເປັນມາຕຣິກເບື້ອງທີ່ ສຳ ຄັນ.
ຮູບແບບດິນຊາຍ Abelian: ຮູບແບບດິນຊາຍແບບ Abelian , ເຊິ່ງເອີ້ນວ່າຕົວແບບ Bak – Tang – Wiesenfeld , ແມ່ນຕົວຢ່າງທີ່ຄົ້ນພົບເປັນຄັ້ງ ທຳ ອິດຂອງລະບົບແບບເຄື່ອນໄຫວທີ່ສະແດງໃຫ້ເຫັນຄວາມ ສຳ ຄັນໃນການຈັດຕັ້ງຕົນເອງ. ມັນໄດ້ຖືກແນະ ນຳ ໂດຍ Per Bak, Chao Tang ແລະ Kurt Wiesenfeld ໃນເຈ້ຍປີ 1987.
ຮູບແບບດິນຊາຍ Abelian: ຮູບແບບດິນຊາຍແບບ Abelian , ເຊິ່ງເອີ້ນວ່າຕົວແບບ Bak – Tang – Wiesenfeld , ແມ່ນຕົວຢ່າງທີ່ຄົ້ນພົບເປັນຄັ້ງ ທຳ ອິດຂອງລະບົບແບບເຄື່ອນໄຫວທີ່ສະແດງໃຫ້ເຫັນຄວາມ ສຳ ຄັນໃນການຈັດຕັ້ງຕົນເອງ. ມັນໄດ້ຖືກແນະ ນຳ ໂດຍ Per Bak, Chao Tang ແລະ Kurt Wiesenfeld ໃນເຈ້ຍປີ 1987.
ແນວພັນ Abelian: ໃນຄະນິດສາດ, ໂດຍສະເພາະໃນເລຂາຄະນິດພຶຊະຄະນິດ, ວິເຄາະສະລັບສັບຊ້ອນແລະທິດສະດີຈໍານວນພຶຊະຄະນິດ, ເປັນແນວພັນ abelian ເປັນຫຼາຍໆພຶຊະຄະນິດຄາດຄະເນວ່າຍັງເປັນກຸ່ມພຶຊະຄະນິດ, ie, ມີກົດຫມາຍວ່າດ້ວຍກຸ່ມທີ່ສາມາດໄດ້ຮັບການກໍານົດໂດຍປະຕິບັດຫນ້າປົກກະຕິ. ແນວພັນ Abelian ແມ່ນໃນເວລາດຽວກັນໃນບັນດາວັດຖຸທີ່ໄດ້ຮັບການສຶກສາຫຼາຍທີ່ສຸດໃນເລຂາຄະນິດພຶດຊະຄະນິດແລະເຄື່ອງມືທີ່ຂາດບໍ່ໄດ້ ສຳ ລັບການຄົ້ນຄວ້າຫຼາຍກ່ຽວກັບຫົວຂໍ້ອື່ນໆໃນເລຂາຄະນິດພຶດຊະຄະນິດແລະທິດສະດີເລກ.
Semigroup: ໃນຄະນິດສາດ, semigroup ແມ່ນໂຄງສ້າງກ່ຽວກັບພຶດຊະຄະນິດເຊິ່ງປະກອບດ້ວຍຊຸດຮ່ວມກັນກັບການປະຕິບັດຖານສອງຄູ່.
Sheaf ຂອງໂມດູນ: ໃນທາງຄະນິດສາດ, sheaf ຂອງ O -modules ຫຼືງ່າຍໆ O -module ທົ່ວພື້ນທີ່ເປັນແຫວນແມ່ນ sheaf F ເຊັ່ນນັ້ນ, ສຳ ລັບຊຸດຍ່ອຍຕ່າງໆຂອງ U , X , F ( U ) ແມ່ນ O ( U ) -module ແລະແຜນທີ່ ຈຳ ກັດ F ( U ) → F ( V ) ເຂົ້າກັນໄດ້ກັບແຜນທີ່ຂໍ້ ຈຳ ກັດ O ( U ) → O ( V ): ການ ຈຳ ກັດຂອງ fs ແມ່ນການ ຈຳ ກັດຂອງເວລາ f ຂອງ s ສຳ ລັບ f ໃນ O ( U ) ແລະ s ໃນ F (U).
ກຸ່ມ Abelian: ໃນຄະນິດສາດ, ກຸ່ມອາເບັນ , ເຊິ່ງເອີ້ນວ່າ ກຸ່ມທີ່ເສີຍເມີຍ , ແມ່ນກຸ່ມ ໜຶ່ງ ເຊິ່ງຜົນຂອງການ ນຳ ໃຊ້ການ ດຳ ເນີນງານຂອງກຸ່ມໃຫ້ກັບສອງອົງປະກອບຂອງກຸ່ມບໍ່ຂື້ນກັບລະບຽບທີ່ພວກເຂົາຂຽນ. ນັ້ນແມ່ນ, ການ ດຳ ເນີນງານຂອງກຸ່ມແມ່ນມີຄວາມ ໝາຍ. ນອກ ເໜືອ ຈາກການປະຕິບັດງານ, ຕົວເລກແລະຕົວເລກຕົວຈິງປະກອບເປັນກຸ່ມຊົນເຜົ່າ abelian, ແລະແນວຄິດຂອງກຸ່ມ abelian ອາດຈະຖືກເບິ່ງວ່າເປັນການລວມຕົວຢ່າງຂອງຕົວຢ່າງເຫຼົ່ານີ້. ກຸ່ມ Abelian ແມ່ນມີຊື່ຕາມນັກຄະນິດສາດນັກຮຽນສະຕະວັດທີ 19 Niels Henrik Abel.
ທິດສະດີທິດສະດີຂອງອາເບນ: ໃນຄະນິດສາດ, ທິດສະດີທິດສະດີຂອງອາເບນ ກ່ຽວຂ້ອງກັບຂີດ ຈຳ ກັດຂອງຊຸດພະລັງງານກັບຜົນລວມຂອງຕົວຄູນຂອງມັນ. ມັນໄດ້ຖືກຕັ້ງຊື່ຕາມນັກຄະນິດສາດຊາວນໍເວ Niels Henrik Abel.
ພື້ນຜິວຂອງ Abelian: ໃນຄະນິດສາດ, ພື້ນຜິວ abelian ແມ່ນແນວພັນ abelian 2 ມິຕິ.
ທິດສະດີທິດສະດີ Abelian ແລະ Tauberian: ໃນວິຊາຄະນິດສາດ, ທິດສະດີທິດສະດີຂອງ Abelian ແລະ Tauberian ແມ່ນທິດສະດີທີ່ໃຫ້ເງື່ອນໄຂ ສຳ ລັບສອງວິທີຂອງການລວມເອົາຊຸດທີ່ແຕກຕ່າງກັນເພື່ອໃຫ້ໄດ້ຜົນດຽວກັນ, ມີຊື່ວ່າ Niels Henrik Abel ແລະ Alfred Tauber. ຕົວຢ່າງຕົ້ນສະບັບແມ່ນທິດສະດີຂອງ Abel ສະແດງໃຫ້ເຫັນວ່າຖ້າຊຸດ ໜຶ່ງ ປ່ຽນໄປໃນຂອບເຂດ ຈຳ ກັດບາງຢ່າງນັ້ນຜົນລວມຂອງ Abel ແມ່ນຂອບເຂດ ຈຳ ກັດດຽວກັນແລະທິດສະດີຂອງ Tauber ສະແດງໃຫ້ເຫັນວ່າຖ້າຜົນບວກຂອງ Abel ມີຕົວຄູນແລະຕົວຄູນມີ ຈຳ ນວນ ໜ້ອຍ ແລ້ວຊຸດດັ່ງກ່າວຈະປ່ຽນເປັນ Abel ຜົນລວມ. ທິດສະດີທິດສະດີທົ່ວໄປຂອງ Abelian ແລະ Tauberian ໃຫ້ຜົນທີ່ຄ້າຍຄືກັນ ສຳ ລັບວິທີການສັງລວມທົ່ວໄປ.
ແນວພັນ Abelian: ໃນຄະນິດສາດ, ໂດຍສະເພາະໃນເລຂາຄະນິດພຶຊະຄະນິດ, ວິເຄາະສະລັບສັບຊ້ອນແລະທິດສະດີຈໍານວນພຶຊະຄະນິດ, ເປັນແນວພັນ abelian ເປັນຫຼາຍໆພຶຊະຄະນິດຄາດຄະເນວ່າຍັງເປັນກຸ່ມພຶຊະຄະນິດ, ie, ມີກົດຫມາຍວ່າດ້ວຍກຸ່ມທີ່ສາມາດໄດ້ຮັບການກໍານົດໂດຍປະຕິບັດຫນ້າປົກກະຕິ. ແນວພັນ Abelian ແມ່ນໃນເວລາດຽວກັນໃນບັນດາວັດຖຸທີ່ໄດ້ຮັບການສຶກສາຫຼາຍທີ່ສຸດໃນເລຂາຄະນິດພຶດຊະຄະນິດແລະເຄື່ອງມືທີ່ຂາດບໍ່ໄດ້ ສຳ ລັບການຄົ້ນຄວ້າຫຼາຍກ່ຽວກັບຫົວຂໍ້ອື່ນໆໃນເລຂາຄະນິດພຶດຊະຄະນິດແລະທິດສະດີເລກ.
ແນວພັນ Abelian: ໃນຄະນິດສາດ, ໂດຍສະເພາະໃນເລຂາຄະນິດພຶຊະຄະນິດ, ວິເຄາະສະລັບສັບຊ້ອນແລະທິດສະດີຈໍານວນພຶຊະຄະນິດ, ເປັນແນວພັນ abelian ເປັນຫຼາຍໆພຶຊະຄະນິດຄາດຄະເນວ່າຍັງເປັນກຸ່ມພຶຊະຄະນິດ, ie, ມີກົດຫມາຍວ່າດ້ວຍກຸ່ມທີ່ສາມາດໄດ້ຮັບການກໍານົດໂດຍປະຕິບັດຫນ້າປົກກະຕິ. ແນວພັນ Abelian ແມ່ນໃນເວລາດຽວກັນໃນບັນດາວັດຖຸທີ່ໄດ້ຮັບການສຶກສາຫຼາຍທີ່ສຸດໃນເລຂາຄະນິດພຶດຊະຄະນິດແລະເຄື່ອງມືທີ່ຂາດບໍ່ໄດ້ ສຳ ລັບການຄົ້ນຄວ້າຫຼາຍກ່ຽວກັບຫົວຂໍ້ອື່ນໆໃນເລຂາຄະນິດພຶດຊະຄະນິດແລະທິດສະດີເລກ.
ທ້ອງຖິ່ນຂອງ ໝວດ ໝູ່: ໃນຄະນິດສາດ, ການແປພາສາທ້ອງຖິ່ນຂອງ ໝວດ ໜຶ່ງ ປະກອບມີການເພີ່ມປະເພດໂມເລກຸນທາງກົງກັນຂ້າມ ສຳ ລັບການສະສົມຂອງໂມເລກຸນບາງຢ່າງ, ຈຳ ກັດພວກມັນໃຫ້ກາຍເປັນ isomorphism ນີ້ແມ່ນຄ້າຍຄືກັນຢ່າງເປັນທາງການກັບຂະບວນການທ້ອງຖິ່ນຂອງແຫວນ; ມັນໂດຍທົ່ວໄປເຮັດໃຫ້ວັດຖຸ isomorphic ທີ່ບໍ່ເຄີຍເປັນມາກ່ອນ. ໃນທິດສະດີ homotopy, ຕົວຢ່າງ, ມີຫຼາຍຕົວຢ່າງຂອງການສ້າງແຜນທີ່ທີ່ບໍ່ສາມາດປ່ຽນແປງໄດ້ເຖິງ homotopy; ແລະຫ້ອງຮຽນທີ່ໃຫຍ່ກວ່າສະຖານທີ່ທຽບເທົ່າ homotopy. ການຄິດໄລ່ສ່ວນປະກອບ ແມ່ນອີກຊື່ ໜຶ່ງ ສຳ ລັບເຮັດວຽກຢູ່ໃນ ໝວດ ໝູ່ ທີ່ໃຊ້ໃນທ້ອງຖິ່ນ.
ແນວພັນ Abelian: ໃນຄະນິດສາດ, ໂດຍສະເພາະໃນເລຂາຄະນິດພຶຊະຄະນິດ, ວິເຄາະສະລັບສັບຊ້ອນແລະທິດສະດີຈໍານວນພຶຊະຄະນິດ, ເປັນແນວພັນ abelian ເປັນຫຼາຍໆພຶຊະຄະນິດຄາດຄະເນວ່າຍັງເປັນກຸ່ມພຶຊະຄະນິດ, ie, ມີກົດຫມາຍວ່າດ້ວຍກຸ່ມທີ່ສາມາດໄດ້ຮັບການກໍານົດໂດຍປະຕິບັດຫນ້າປົກກະຕິ. ແນວພັນ Abelian ແມ່ນໃນເວລາດຽວກັນໃນບັນດາວັດຖຸທີ່ໄດ້ຮັບການສຶກສາຫຼາຍທີ່ສຸດໃນເລຂາຄະນິດພຶດຊະຄະນິດແລະເຄື່ອງມືທີ່ຂາດບໍ່ໄດ້ ສຳ ລັບການຄົ້ນຄວ້າຫຼາຍກ່ຽວກັບຫົວຂໍ້ອື່ນໆໃນເລຂາຄະນິດພຶດຊະຄະນິດແລະທິດສະດີເລກ.
ການຄູນສະລັບສັບຊ້ອນຂອງແນວພັນ abelian: ໃນທາງຄະນິດສາດ, ແນວພັນທີ່ຜິດປົກກະຕິ A ທີ່ ຖືກ ກຳ ນົດໃນພາກສະ ໜາມ K ຖືກກ່າວເຖິງວ່າມີ ຊະນິດ CM ຖ້າມັນມີຂະ ໜາດ ໃຫຍ່ພໍສົມຄວນໃນວົງແຫວນ endomorphism End ( A ). ຄຳ ສັບໃນ ຄຳ ນີ້ແມ່ນມາຈາກທິດສະດີຄູນສະລັບສັບຊ້ອນ, ເຊິ່ງຖືກພັດທະນາ ສຳ ລັບເສັ້ນໂຄ້ງຮູບຮີໃນສະຕະວັດທີສິບເກົ້າ. ໜຶ່ງ ໃນບັນດາຜົນ ສຳ ເລັດທີ່ ສຳ ຄັນໃນທິດສະດີເລກຄະນິດສາດແລະເລຂາຄະນິດພຶດຊະຄະນິດຂອງສັດຕະວັດທີ 20 ແມ່ນການຊອກຫາຮູບແບບທີ່ຖືກຕ້ອງຂອງທິດສະດີທີ່ສອດຄ້ອງກັນ ສຳ ລັບແນວພັນອະໄວຍະວະຂອງ abelian ຂອງມິຕິ d > 1. ບັນຫາແມ່ນຢູ່ໃນລະດັບທີ່ເລິກເຊິ່ງຂອງການບໍ່ເອົາໃຈໃສ່, ເພາະມັນຍາກຫຼາຍ ເພື່ອ ໝູນ ໃຊ້ ໜ້າ ທີ່ການວິເຄາະຂອງຕົວແປທີ່ສັບສົນຫຼາຍຢ່າງ.
ຄະນິດສາດ Abelian von Neumann: ໃນການວິເຄາະທີ່ເປັນປະໂຫຍດ, ເປັນ abelian von Neumann ພຶດຊະຄະນິດເປັນພຶດຊະຄະນິດ von Neumann ຂອງຜູ້ປະກອບການກ່ຽວກັບການເປັນພື້ນທີ່ Hilbert ທີ່ອົງປະກອບທັງຫມົດຍ່າງ.
ຄະນິດສາດ Abelian von Neumann: ໃນການວິເຄາະທີ່ເປັນປະໂຫຍດ, ເປັນ abelian von Neumann ພຶດຊະຄະນິດເປັນພຶດຊະຄະນິດ von Neumann ຂອງຜູ້ປະກອບການກ່ຽວກັບການເປັນພື້ນທີ່ Hilbert ທີ່ອົງປະກອບທັງຫມົດຍ່າງ.
ກຸ່ມຍ່ອຍ: ໃນຄະນິດສາດ, ໂດຍສະເພາະໃນຄະນິດສາດທີ່ບໍ່ມີຕົວຕົນ, ກຸ່ມຍ່ອຍ ຫລື ກຸ່ມຍ່ອຍທີ່ມາຈາກ ກຸ່ມແມ່ນກຸ່ມຍ່ອຍທີ່ຜະລິດໂດຍຜູ້ ກຳ ນົດການທັງ ໝົດ ຂອງກຸ່ມ.
ກຸ່ມຍ່ອຍ: ໃນຄະນິດສາດ, ໂດຍສະເພາະໃນຄະນິດສາດທີ່ບໍ່ມີຕົວຕົນ, ກຸ່ມຍ່ອຍ ຫລື ກຸ່ມຍ່ອຍທີ່ມາຈາກ ກຸ່ມແມ່ນກຸ່ມຍ່ອຍທີ່ຜະລິດໂດຍຜູ້ ກຳ ນົດການທັງ ໝົດ ຂອງກຸ່ມ.
Abelians: Abelians ແມ່ນນິກາຍຄຣິສຕຽນທີ່ເກີດຂື້ນໃນສະຕະວັດທີ 4 ໃນເຂດຊົນນະບົດໃກ້ກັບ Hippo Regius ໃນພາກ ເໜືອ ຂອງອາຟຣິກກາໃນໄລຍະການປົກຄອງຂອງ Arcadius. ພວກເຂົາ ດຳ ລົງຊີວິດຢູ່ໃນທະວີບອາເມລິກາດັ່ງທີ່ພວກເຂົາຢືນຢັນວ່າອາເບນໄດ້ເຮັດ. ພວກເຂົາຖືກຮຽກຮ້ອງໃຫ້ແຕ່ງງານແຕ່ຖືກຫ້າມບໍ່ໃຫ້ແຕ່ງງານກັບຜົວ. ແຕ່ລະຄູ່ມີຄວາມຕ້ອງການລ້ຽງດູລູກສອງຄົນ, ຊາຍແລະຍິງ. ເມື່ອພໍ່ແມ່ລ້ຽງຂອງພວກເຂົາໄດ້ເສຍຊີວິດ, ຜູ້ລ້ຽງດູລູກເຫຼົ່ານີ້ຈະແຕ່ງຕັ້ງເປັນຄູ່ແລະເອົາລູກອີກສອງຄົນ. ເນື່ອງຈາກວ່າບໍ່ມີເດັກນ້ອຍຂອງອາເບນໄດ້ຖືກກ່າວເຖິງໃນພຣະ ຄຳ ພີ, ພວກອາເບນຖືວ່າລາວບໍ່ມີ. ທັດສະນະນີ້ໄດ້ຮັບອິດທິພົນຈາກຊາວຢິວ, ແລະທັດສະນະຂອງ Gnostic ທີ່ດົນໃຈໂດຍ Manichean ກ່ຽວກັບ Abel ທີ່ໄດ້ຮັບຮູ້ວ່າ, ໃນຂະນະທີ່ລາວແຕ່ງງານ, ລາວຍັງຄົງເປັນຍິງສາວ. ບັນທຶກສະເພາະຂອງນິກາຍພຽງແຕ່ແມ່ນໃນ Augustine ຂອງ De Haereticis ch. 87 , ບ່ອນທີ່ລາວຂຽນວ່າຊື່ຂອງນິກາຍອາດຈະແມ່ນຕົ້ນກໍາເນີດຂອງ Punic. ອີງຕາມການ Augustine, ນິກາຍໄດ້ສູນພັນໄປໃນປີ 428 ເມື່ອສະມາຊິກຄົນສຸດທ້າຍປ່ຽນມາເປັນສາສະ ໜາ ກາໂຕລິກ.
Abelichnus: Abelichnus ແມ່ນ ichnogenus ທີ່ສູນພັນໄປດ້ວຍຮອຍຕີນຂອງໄດໂນເສົາຈາກ Candeleros Formation ແລະ Rio Limay Formation. ປະເພດ ichnospecies, Abelichnus astigerrae , ຖືກຄົ້ນພົບເປັນຄັ້ງ ທຳ ອິດໃນປະເທດອາເຈນຕິນາແລະຖືກບັນທຶກເປັນຮອຍຕີນໄດໂນເສົາທີ່ມີຊື່ສຽງທີ່ໃຫຍ່ທີ່ສຸດທີ່ເຄີຍຄົ້ນພົບ Abelichnus ອາດຈະເຕີບໃຫຍ່ຂະ ໜາດ ຄວາມຍາວ 12,5-13 ແມັດ.
Abelin: Abelin ແມ່ນນາມສະກຸນ, ແລະອາດຈະອ້າງເຖິງ: Jean-Pierre Abelin, ນັກການເມືອງຝຣັ່ງ Johann Philipp Abelin, ນັກປະຫວັດສາດເຢຍລະມັນ Ernst Abelin, psychoanalyst ຂອງປະເທດສະວິດແລະເປັນຜູ້ກໍ່ຕັ້ງທິດສະດີຂອງຕົ້ນສາມຫລ່ຽມຕົ້ນ
Jean-Pierre Abelin: Jean-Pierre Abelin ແມ່ນນັກການເມືອງຝຣັ່ງ.
ຕິກິຣິຍາ Abelin: ປະ ຕິກິລິຍາຂອງ Abelin ແມ່ນປະຕິກິລິຍາທາງດ້ານຄຸນນະພາບ ສຳ ລັບການສະແດງໃຫ້ເຫັນການມີທາດ Arsphenamine ແລະ neoarsphenamine ໃນເລືອດແລະປັດສະວະ.