Archilema vilis, Archileptocera, Leptopus

Archilema vilis: Archilema vilis ແມ່ນ ແມງກະເບື້ອ ຂອງ Arctiinae ທີ່ອະທິບາຍຄັ້ງ ທຳ ອິດໂດຍ Sven Jorgen R. Birket-Smith ໃນປີ 1965. ມັນພົບຢູ່ໄນຈີເຣຍ.
Archileptocera: Archileptocera ແມ່ນສະກຸນຂອງແມງວັນທີ່ເປັນຂອງຄອບຄົວ Sphaeroceridae, ຂີ້ແມງວັນ ໜ້ອຍ.
Leptopus: Leptopus , maidenbushes ແມ່ນກຸ່ມຂອງພືດໃນຄອບຄົວຕົ້ນດອກໄມ້ Phyllanthaceae ໄດ້ຖືກອະທິບາຍວ່າເປັນສະກຸນໃນປີ 1836.
Archilestes: Archilestes ແມ່ນສະກຸນຂອງ damselflies ໃນ Lestidae ຄອບຄົວ. ເຊັ່ນດຽວກັນກັບສະມາຊິກສ່ວນໃຫຍ່ຂອງ Lestidae, Archliestes ພັກຜ່ອນດ້ວຍປີກຂອງພວກມັນກະແຈກກະຈາຍ. ສະກຸນນີ້ມີແປດຊະນິດ, ການແຜ່ກະຈາຍທີ່ຍິ່ງໃຫຍ່ແລະ California Spreadwing ແມ່ນພົບຫຼາຍທີ່ສຸດແລະແຜ່ຫຼາຍ.
ແຄວ້ນ Archilestes: Archilestes californicus , ການແຜ່ກະຈາຍຂອງ California , ແມ່ນຊະນິດ ໜຶ່ງ ຂອງການແຜ່ກະຈາຍໃນ Lestidae ຄອບຄົວທີ່ ທຳ ລາຍຕົວເອງ. ມັນໄດ້ຖືກພົບເຫັນຢູ່ໃນອາເມລິກາກາງແລະອາເມລິກາເຫນືອ.
ອະໄວຍະວະ Archilestes: Archilestes exoletus ແມ່ນຊະນິດ ໜຶ່ງ ຂອງການແຜ່ກະຈາຍໃນ Lestidae ຄອບຄົວທີ່ ທຳ ລາຍຕົວເອງ. ມັນໄດ້ຖືກພົບເຫັນຢູ່ໃນອາເມລິກາໃຕ້.
ເຜີຍແຜ່ທີ່ຍິ່ງໃຫຍ່: ການ ແຜ່ກະຈາຍທີ່ຍິ່ງໃຫຍ່ ແມ່ນສ້າງຄວາມເສຍຫາຍໃນຄອບຄົວ Lestidae. ໃນເວລາທີ່ການແຜ່ກະຈາຍທີ່ຍິ່ງໃຫຍ່ໄດ້ຖືກເຮັດໃຫ້ຕົກໃຈພວກເຂົາມັກຈະກັບຄືນໄປບ່ອນຂອງ perch ຫຼື perch ໃກ້ຄຽງ.
guayaraca Archilestes: Archilestes guayaraca ແມ່ນຊະນິດ ໜຶ່ງ ຂອງການແຜ່ກະຈາຍໃນ Lestidae ຄອບຄົວທີ່ ທຳ ລາຍຕົວເອງ. ມັນໄດ້ຖືກພົບເຫັນຢູ່ໃນອາເມລິກາໃຕ້.
ປະຕິທິນ latilates: Archilestes latialatus ແມ່ນຊະນິດ ໜຶ່ງ ຂອງການແຜ່ກະຈາຍໃນ Lestidae ຄອບຄົວທີ່ ທຳ ລາຍຕົວເອງ. ມັນໄດ້ຖືກພົບເຫັນຢູ່ໃນອາເມລິກາກາງ.
neblina Archilestes: Archilestes neblina ແມ່ນຊະນິດ ໜຶ່ງ ຂອງການແຜ່ກະຈາຍໃນ Lestidae ຄອບຄົວທີ່ ທຳ ລາຍຕົວເອງ. ມັນໄດ້ຖືກພົບເຫັນຢູ່ໃນອາເມລິກາກາງ.
Archilestes regalis: Archilestes regalis ແມ່ນຊະນິດ ໜຶ່ງ ຂອງການແຜ່ກະຈາຍໃນ Lestidae ຄອບຄົວທີ່ ທຳ ລາຍຕົວເອງ. ມັນໄດ້ຖືກພົບເຫັນຢູ່ໃນອາເມລິກາກາງ.
ທໍ່ລະບົບປະສາດ: Archilestes tuberalatus ແມ່ນຊະນິດ ໜຶ່ງ ຂອງການແຜ່ກະຈາຍໃນ Lestidae ຄອບຄົວທີ່ ທຳ ລາຍຕົວເອງ.
Archilestris: Archilestris ແມ່ນສະກຸນຂອງໂຈນປຸ້ນບິນໃນຄອບຄົວ Asilidae. ມີປະມານຫົກຊະນິດທີ່ຖືກພັນລະນາໃນ Archilestris .
ຂະ ໜາດ ໃຫຍ່ Archilestris: Archilestris magnificus ແມ່ນຊະນິດຂອງໂຈນປຸ້ນບິນໃນຄອບຄົວ Asilidae.
Austrolimnophila: Austrolimnophila ແມ່ນສະກຸນຂອງ crane ບິນໃນຄອບຄົວ Limoniidae.
ທາດແປ້ງທາດໂພແທດຊຽມ: ໂພແທດຊຽມ tartrate , dipot potassium tartrate ຫຼື argol ມີສູດ K 2 C 4 H 4 O 6 . ມັນແມ່ນເກືອໂພແທດຊຽມຂອງອາຊິດທາຕາລິກ. ມັນມັກຈະສັບສົນກັບທາດໂປຼຕີນຈາກທາດໂພແທດຊຽມ, ເຊິ່ງເອີ້ນກັນວ່າຄີມທາຕາ. ໃນຖານະທີ່ເປັນອາຫານເສີມ, ມັນແບ່ງປັນຕົວເລກ E E336 ກັບທາດໂປຼຕີນຈາກທາດໂປຼຕຽມ.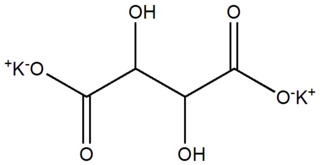
Archilobesia: Archilobesia ແມ່ນສະກຸນຂອງແມງກະເບື້ອທີ່ຂຶ້ນກັບ subfamily Olethreutinae ຂອງຄອບຄົວ Tortricidae.
Archilobesia doboszi: Archilobesia doboszi ແມ່ນຊະນິດຂອງແມງກະ ເບື້ອ ຂອງຄອບຄົວ Tortricidae. ມັນໄດ້ຖືກພົບເຫັນຢູ່ໃນ New Caledonia ໃນພາກຕາເວັນຕົກສຽງໃຕ້ຂອງມະຫາສະ ໝຸດ ປາຊີຟິກ. ທີ່ຢູ່ອາໄສປະກອບດ້ວຍປ່າໄມ້ຝົນ.
Archilochian: Archilochian ຫຼື archilochean ແມ່ນ ຄຳ ສັບທີ່ໃຊ້ໃນການວິເຄາະມິຕິຂອງກະວີແລະພາສາລາແຕັງບູຮານ. ຊື່ດັ່ງກ່າວແມ່ນໄດ້ມາຈາກ Archilochus, ເຊິ່ງບົດກະວີຂອງລາວໃຊ້ຈັງຫວະ ທຳ ອິດ.
Archilochian: Archilochian ຫຼື archilochean ແມ່ນ ຄຳ ສັບທີ່ໃຊ້ໃນການວິເຄາະມິຕິຂອງກະວີແລະພາສາລາແຕັງບູຮານ. ຊື່ດັ່ງກ່າວແມ່ນໄດ້ມາຈາກ Archilochus, ເຊິ່ງບົດກະວີຂອງລາວໃຊ້ຈັງຫວະ ທຳ ອິດ.
Archilochus: Archilochus ແມ່ນນັກກະວີບົດເພງກະເຣັກຂອງຍຸກ Archaic ຈາກເກາະ Paros. ລາວໄດ້ຮັບການສະຫລອງ ສຳ ລັບການໃຊ້ມວຍ poetic ທີ່ມີຄວາມຫລາກຫລາຍແລະມີລັກສະນະ ໃໝ່, ແລະເປັນນັກຂຽນຊາວກະເຣັກທີ່ຮູ້ຈັກກັນໃນ ທຳ ອິດທີ່ປະກອບເກືອບທັງ ໝົດ ໃນຫົວຂໍ້ຂອງອາລົມແລະປະສົບການຂອງລາວເອງ.
Archilochus: Archilochus ແມ່ນນັກກະວີບົດເພງກະເຣັກຂອງຍຸກ Archaic ຈາກເກາະ Paros. ລາວໄດ້ຮັບການສະຫລອງ ສຳ ລັບການໃຊ້ມວຍ poetic ທີ່ມີຄວາມຫລາກຫລາຍແລະມີລັກສະນະ ໃໝ່, ແລະເປັນນັກຂຽນຊາວກະເຣັກທີ່ຮູ້ຈັກກັນໃນ ທຳ ອິດທີ່ປະກອບເກືອບທັງ ໝົດ ໃນຫົວຂໍ້ຂອງອາລົມແລະປະສົບການຂອງລາວເອງ.
Archilochus: Archilochus ແມ່ນນັກກະວີບົດເພງກະເຣັກຂອງຍຸກ Archaic ຈາກເກາະ Paros. ລາວໄດ້ຮັບການສະຫລອງ ສຳ ລັບການໃຊ້ມວຍ poetic ທີ່ມີຄວາມຫລາກຫລາຍແລະມີລັກສະນະ ໃໝ່, ແລະເປັນນັກຂຽນຊາວກະເຣັກທີ່ຮູ້ຈັກກັນໃນ ທຳ ອິດທີ່ປະກອບເກືອບທັງ ໝົດ ໃນຫົວຂໍ້ຂອງອາລົມແລະປະສົບການຂອງລາວເອງ.
Archilochus (ນົກ): Archilochus ແມ່ນສະກຸນຂອງ hummingbirds. ມັນປະກອບມີສອງຊະນິດເຄື່ອນຍ້າຍນ້ອຍໆທີ່ມີສາຍພັນໃນອາເມລິກາ ເໜືອ ແລະລະດູ ໜາວ ໃນອາເມລິກາກາງ, ແມັກຊິໂກແລະພາກໃຕ້ຂອງສະຫະລັດອາເມລິກາ.
Archilochus (ນົກ): Archilochus ແມ່ນສະກຸນຂອງ hummingbirds. ມັນປະກອບມີສອງຊະນິດເຄື່ອນຍ້າຍນ້ອຍໆທີ່ມີສາຍພັນໃນອາເມລິກາ ເໜືອ ແລະລະດູ ໜາວ ໃນອາເມລິກາກາງ, ແມັກຊິໂກແລະພາກໃຕ້ຂອງສະຫະລັດອາເມລິກາ.
ກະດິງ ດຳ ສີ ດຳ: ກະ ດິງປີກ ດຳ ດຳ ແມ່ນສັດລ້ຽງລູກດ້ວຍນ້ ຳ ນົມ ຂະ ໜາດ ນ້ອຍທີ່ອາໄສຢູ່ໃນວົງກວ້າງ. ມັນແມ່ນການເຄື່ອນຍ້າຍ, ໃຊ້ເວລາໃນລະດູ ໜາວ ໄກຮອດພາກໃຕ້ຂອງປະເທດແມັກຊິໂກ.
Rubming ສີຂີ້ເຖົ່າຄໍ: ຕົ້ນ ເຜິ້ງທີ່ມີລົມເຢັນ ເປັນຊະນິດທີ່ມີຄວາມຊຸ່ມຊື່ນໂດຍທົ່ວໄປໃຊ້ຈ່າຍໃນລະດູ ໜາວ ໃນອາເມລິກາກາງ, ແມັກຊິໂກແລະ Florida, ແລະເຄື່ອນຍ້າຍໄປປະເທດການາດາແລະພາກສ່ວນອື່ນໆຂອງອາເມລິກາຕາເວັນອອກ ເໜືອ ເພື່ອລະດູຮ້ອນ. ມັນແມ່ນບ່ອນທີ່ພົບເຫັນ ທຳ ມະດາທີ່ພົບເຫັນຫລາຍທີ່ສຸດທາງຕາເວັນອອກຂອງແມ່ນ້ ຳ Mississippi ໃນອາເມລິກາ ເໜືອ.
Archilochus: Archilochus ແມ່ນນັກກະວີບົດເພງກະເຣັກຂອງຍຸກ Archaic ຈາກເກາະ Paros. ລາວໄດ້ຮັບການສະຫລອງ ສຳ ລັບການໃຊ້ມວຍ poetic ທີ່ມີຄວາມຫລາກຫລາຍແລະມີລັກສະນະ ໃໝ່, ແລະເປັນນັກຂຽນຊາວກະເຣັກທີ່ຮູ້ຈັກກັນໃນ ທຳ ອິດທີ່ປະກອບເກືອບທັງ ໝົດ ໃນຫົວຂໍ້ຂອງອາລົມແລະປະສົບການຂອງລາວເອງ.
Archilochus: Archilochus ແມ່ນນັກກະວີບົດເພງກະເຣັກຂອງຍຸກ Archaic ຈາກເກາະ Paros. ລາວໄດ້ຮັບການສະຫລອງ ສຳ ລັບການໃຊ້ມວຍ poetic ທີ່ມີຄວາມຫລາກຫລາຍແລະມີລັກສະນະ ໃໝ່, ແລະເປັນນັກຂຽນຊາວກະເຣັກທີ່ຮູ້ຈັກກັນໃນ ທຳ ອິດທີ່ປະກອບເກືອບທັງ ໝົດ ໃນຫົວຂໍ້ຂອງອາລົມແລະປະສົບການຂອງລາວເອງ.
Archilochian: Archilochian ຫຼື archilochean ແມ່ນ ຄຳ ສັບທີ່ໃຊ້ໃນການວິເຄາະມິຕິຂອງກະວີແລະພາສາລາແຕັງບູຮານ. ຊື່ດັ່ງກ່າວແມ່ນໄດ້ມາຈາກ Archilochus, ເຊິ່ງບົດກະວີຂອງລາວໃຊ້ຈັງຫວະ ທຳ ອິດ.
Archlute: The archlute ແມ່ນເຄື່ອງມືຊ່ອຍແນ່ທີ່ ຍຶດ ໄດ້ຈາກເອີຣົບທີ່ຖືກພັດທະນາຂື້ນປະມານ 1600 ເປັນການປະນີປະນອມລະຫວ່າງ theorbo ທີ່ມີຂະ ໜາດ ໃຫຍ່ຫຼາຍ, ຂະ ໜາດ ແລະການປ້ອນຂໍ້ມູນຄືນ ໃໝ່ ເຊິ່ງເຮັດໃຫ້ມີຄວາມຫຍຸ້ງຍາກໃນການປະຕິບັດງານດົນຕີດ່ຽວ, ແລະ Renaissance tenor lute, ເຊິ່ງຂາດລະດັບສຽງຂອງສຽງເບດ. ຂອງ theorbo ໄດ້. ໂດຍເນື້ອແທ້ແລ້ວຂອງ lute tenor ກັບການຂະຫຍາຍຄໍຂອງ theorbo, archlute ຂາດພະລັງງານໃນ tenor ແລະ bass ທີ່ຮ່າງກາຍໃຫຍ່ຂອງ theorbo ແລະປົກກະຕິມີຄວາມຍາວສູງກວ່າ string.
Archilycus: ໃນນິທານເລື່ອງເຣັກ, Archilycus ຫຼື Areilycus , ແມ່ນບິດາຂອງ Archesilaus ແລະ Prothoenor, ເຊິ່ງເປັນຜູ້ ນຳ ຂອງໂບໂບອານໃນການເລັ່ງລັດຕໍ່ Troy. ພໍ່ຂອງລາວແມ່ນ Itonus, ລູກຊາຍຂອງ Boeotus ໃນຂະນະທີ່ອ້າຍຂອງລາວແມ່ນ Hippalcimus, Electryon, ແລະ Alegenor.
Archim: Archim ແມ່ນໂປແກຼມຟຣີ ສຳ ລັບສ້າງເສັ້ນສະແດງເປັນສອງຫລືສາມຂະ ໜາດ. ມັນມີຄວາມສາມາດໃນກາຟິກທີ່ຊັດເຈນແລະ parametric ແລະ ນຳ ໃຊ້ຮູບແບບທີ່ມີລະຫັດ ສຳ ລັບການປ້ອນຂໍ້ມູນກ່ຽວກັບ ໜ້າ ທີ່, ສະນັ້ນເສັ້ນສະແດງໃນການປະສານງານຂົ້ວໂລກກາຍເປັນກໍລະນີສະເພາະຂອງກາຟິກ parametric
Macrostomidae: The Macrostomidae ແມ່ນຄອບຄົວຂອງແມ່ພະຍາດແມ່ທ້ອງນ້ອຍໆທີ່ອາໃສຢູ່ໃຕ້ນ້ ຳ, ແລະສະມາຊິກໃນທະເລ, ນ້ ຳ ຕົກ, ນ້ ຳ ຈືດ. ໃນປະຈຸບັນນີ້ມີປະມານ 180 ຊະນິດທີ່ມີຊື່ໃນຄອບຄົວນີ້.
Archimaga: Archimaga ແມ່ນສະກຸນຂອງແມງໄມ້ທີ່ເປັນຂອງຄອບຄົວ Tortricidae.
ໝາກ ກອກ Metrernis: ຕົ້ນໄມ້ Metrernis ochrolina ແມ່ນຊະນິດຂອງແມງກະ ເບື້ອ ຂອງຄອບຄົວ Tortricidae ອະທິບາຍຄັ້ງ ທຳ ອິດໂດຍ Edward Meyrick ໃນປີ 1906. ມັນພົບໃນປະເທດສີລັງກາ.
ປັດຊະຍາ Archimaga: Archimaga philomina ແມ່ນແມງໄມ້ຊະນິດ ໜຶ່ງ ຂອງຄອບຄົວ Tortricidae. ມັນຖືກພົບເຫັນຢູ່ເມືອງ Assam, ປະເທດອິນເດຍ.
Archimaga pyractis: Archimaga pyractis ແມ່ນຊະນິດຂອງແມງກະ ເບື້ອ ຂອງຄອບຄົວ Tortricidae. ມັນຖືກພົບເຫັນຢູ່ໃນປະເທດສີລັງກາ.
Archimage: Archimage ແມ່ນສະຕູດິໂອສິລະປະສາຍຕາທີ່ໃຊ້ໃນ Houston ເຊິ່ງໄດ້ ນຳ ໃຊ້ປະສົບການຂອງຕົນໃນສະຖາປັດຕະຍະ ກຳ ຄອມພິວເຕີ້ເພື່ອຊ່ຽວຊານໃນການພັດທະນາ Serious Video Game ເພື່ອຊຸມຊົນຄົ້ນຄ້ວາການແພດ. Archimage ສ້າງ Escape From Diab ແລະ Nanoswarm: ການສະແດງຈາກ Inner Space , ເກມ PC ສອງພັນລ້ານ ໂດລ້າທີ່ ໄດ້ຮັບການສະ ໜັບ ສະ ໜູນ ຈາກສະຖາບັນສຸຂະພາບແຫ່ງຊາດເພື່ອຕ້ານໂລກອ້ວນແລະໂລກເບົາຫວານປະເພດ 2 ໃນເດັກນ້ອຍ.
Magician (ປັນ): A magician, ຊຶ່ງເອີ້ນກັນວ່າເປັນ mage, warlock, witch, ຂອງຄວາມຍາວປາ / wizardess, enchanting / ສະເຫນ່, sorcerer / sorceress ຫຼືສະກົດຄໍາລໍ້, ແມ່ນຜູ້ທີ່ນໍາໃຊ້ຫຼືການປະຕິບັດ magic ຈາກ supernatural, occult, ຫຼືປ້ອນແຫຼ່ງຂໍ້ມູນ. ບັນດານັກປັນຍາຊົນແມ່ນຕົວເລກທົ່ວໄປໃນວຽກງານຂອງຈິນຕະນາການ, ເຊັ່ນ: ວັນນະຄະດີຈິນຕະນາການແລະເກມທີ່ມີບົດບາດ, ແລະເພີດເພີນກັບປະຫວັດສາດທີ່ອຸດົມສົມບູນໃນເລື່ອງນິທານ, ນິທານ, ນິທານ, ແລະນິທານພື້ນເມືອງ.
Archimago: Archimago ແມ່ນ ໝໍ ຜີໃນ The Faerie Queene ໂດຍ Edmund Spenser. ໃນການບັນຍາຍດັ່ງກ່າວ, ລາວໄດ້ມີສ່ວນຮ່ວມຢ່າງຕໍ່ເນື່ອງໃນການເຮັດກົນອຸປະກອນທີ່ຫຼອກລວງ, ຄືກັບວ່າລາວເຮັດ Una ທີ່ບໍ່ຖືກຕ້ອງເພື່ອລໍ້ລວງ Knight Red-Cross Knight ເຂົ້າໄປໃນຄວາມໂລບ, ແລະເມື່ອສິ່ງນີ້ລົ້ມເຫລວ, ສົມທົບກັບຮູບພາບອື່ນ, ຂອງການຫຼອກລວງ, ເພື່ອຫຼອກລວງຜູ້ທີ່ເຊື່ອໃນ Una ແມ່ນບໍ່ຖືກຕ້ອງກັບເຂົາ.
çrçiman: çrçiman ແມ່ນ ໝູ່ ບ້ານແລະເທດສະບານໃນເມືອງ Shamakhi Rayon ຂອງປະເທດ Azerbaijan. ມັນມີປະຊາກອນທັງ ໝົດ 587 ຄົນ.
Archimandrite: Archimandrite ຫົວຂໍ້, ໃຊ້ໃນໂບດຄຣິສຕະຈັກຕາເວັນອອກ, ໃນເບື້ອງຕົ້ນໄດ້ກ່າວເຖິງພຣະອາຈານໃຫຍ່ຜູ້ ໜຶ່ງ ທີ່ອະທິການໄດ້ແຕ່ງຕັ້ງໃຫ້ຄວບຄຸມໂບດແລະວັດວາອາຮາມຫຼາຍແຫ່ງ, ຫຼືຕໍ່ພະອາຈານຂອງບາງວັດທີ່ຍິ່ງໃຫຍ່ແລະ ສຳ ຄັນ.
Pano Archimandrita: Pano Archimandrita ແມ່ນບ້ານ ໜຶ່ງ ໃນເມືອງ Paphos ຂອງ Cyprus, ຕັ້ງຢູ່ທາງທິດຕາເວັນອອກສ່ຽງ ເໜືອ ປະມານ 12 ກິໂລແມັດ.
Archimandrite: Archimandrite ຫົວຂໍ້, ໃຊ້ໃນໂບດຄຣິສຕະຈັກຕາເວັນອອກ, ໃນເບື້ອງຕົ້ນໄດ້ກ່າວເຖິງພຣະອາຈານໃຫຍ່ຜູ້ ໜຶ່ງ ທີ່ອະທິການໄດ້ແຕ່ງຕັ້ງໃຫ້ຄວບຄຸມໂບດແລະວັດວາອາຮາມຫຼາຍແຫ່ງ, ຫຼືຕໍ່ພະອາຈານຂອງບາງວັດທີ່ຍິ່ງໃຫຍ່ແລະ ສຳ ຄັນ.
Boniface Luykx: Boniface Joseph Luykx ແມ່ນປະໂລຫິດ Norbertine ໃນປະເທດແບນຊິກ, ຜູ້ຊ່ຽວຊານດ້ານ liturgical Roman, ແລະຜູ້ກໍ່ຕັ້ງ / Hegumen ຂອງໂບດກາໂຕລິກ rite ອູແກຣນໃນພາກເຫນືອ California. polyglot, ລາວມີຄວາມຊົງ ຈຳ ໃນການຖ່າຍຮູບແລະເປັນເຄື່ອງມືໃນການກະຕຸ້ນແລະກະກຽມ ສຳ ລັບວາຕິກັນ II.
Cyril Pavlov: Cyril Pavlov , ແອວເດີ Cyril , ໃນຊີວິດ: Ivan Dmitrievich Pavlov , ແມ່ນຄົນຄຣິດສະຕຽນແບບດັ້ງເດີມຂອງລັດເຊຍ, ຜູ້ເຖົ້າ, ຜູ້ປະຫລາດໃຈແລະ Archimandrite, ຜູ້ທີ່ໄດ້ຮັບສາລະພາບກັບ Patriarch Alexy II. ທ່ານຍັງໄດ້ສາລະພາບຕໍ່ບັນພະບຸລຸດຄົນກ່ອນ ໜ້າ ນີ້ຄື Alexy I ແລະ Pimen.
Joasaph (McLellan): Archimandrite Joasaph ແມ່ນນັກວິຊາການອາເມລິກາແລະປະໂລຫິດຂອງໂບດ Orthodox ລັດເຊຍຢູ່ນອກຣັດເຊຍໃນປີສຸດທ້າຍຂອງຊີວິດຂອງລາວ. ຕັ້ງແຕ່ເດືອນກຸມພາປີ 2009 ຈົນເຖິງການເສຍຊີວິດຂອງລາວທ່ານໄດ້ ດຳ ລົງ ຕຳ ແໜ່ງ ເປັນຫົວ ໜ້າ ຄະນະຜູ້ສອນສາດສະ ໜາ ລັດເຊຍແບບດັ້ງເດີມຢູ່ກຸງເຢຣູຊາເລັມຂອງໂບດ Orthodox ລັດເຊຍຢູ່ນອກຣັດເຊຍ.
Archimandrite Kyprianos: Archimandrite Kyprianos ແມ່ນນັກຂຽນ, ນັກປະຫວັດສາດ, ນັກກະວີ, ແລະບັນນາທິການເຜີຍແຜ່. ລາວແມ່ນ ໜຶ່ງ ໃນບັນດານັກປັນຍາຊົນແລະນັກສືກສາ Cypriot ກເຣັກທີ່ ສຳ ຄັນຂອງສະຕະວັດທີ 18.
Grigol Peradze: Saint Grigol Peradze ແມ່ນຕົວເລກດ້ານສາດສະ ໜາ ທີ່ມີຊື່ສຽງຂອງ ໂຈເຊັບ , ນັກປັດຊະຍາ, ນັກວິທະຍາສາດ, ນັກປະຫວັດສາດ, ແລະສາດສະດາຈານດ້ານສິດທິບັດໃນຍຸກສົງຄາມ.
Archimandrite Photius: Archimandrite Photius , ເກີດ Petr Nikitich Spassky , ແມ່ນປະໂລຫິດທີ່ມີອິດທິພົນແລະມີປະຕິກິລິຍາແລະມີຄວາມລຶກລັບ, ໄດ້ຮັບການແຕ່ງຕັ້ງ 1822 Archimandrite ຂອງ Saint George ຫຼື Yuriev Monastery ໃນ Novgorod. ແຕ່ປີ 1823 ເຖິງປີ 1825, ທ່ານແລະທ່ານ Alexey Arakcheyev ໄດ້ວາງແຜນການລົ້ມລະລາຍຂອງຄູ່ແຂ່ງທາງການເມືອງຂອງ Arakcheyev, ທ່ານ Alexander Nikolaevich Golitsyn, ລັດຖະມົນຕີກະຊວງສຶກສາທິການແລະການເມືອງ. ເຊັ່ນດຽວກັນກັບການປົກຄອງຂອງ Tsar Nicholas II ໃນເວລາຕໍ່ມາ, ນີ້ແມ່ນຍຸກແຫ່ງການກະບົດ, ການຕໍ່ຕ້ານແລະການຂັດແຍ້ງແລະການໂຕ້ຖຽງກັນ, ແລະ Photius, "ລັກສະນະລະຄອນແລະ hypnotic", ໄດ້ຖືກປຽບທຽບກັບ Rasputin.
Sophrony (Sakharov): ໄພ່ພົນ Sophrony , ທີ່ເອີ້ນກັນວ່າ ແອວເດີ Sophrony ຫຼື ພໍ່ Sophrony ແມ່ນ archimandrite ແລະ ໜຶ່ງ ໃນບັນດານັກບວດ Christian ທີ່ສັງເກດເຫັນໃນສະຕະວັດທີ 20. ລາວເປັນທີ່ຮູ້ຈັກດີທີ່ສຸດວ່າເປັນສານຸສິດແລະນັກຂຽນຊີວະປະຫວັດຂອງ St Silouan the Athonite ແລະນັກຂຽນຂອງ St Silouan, ແລະເປັນຜູ້ກໍ່ຕັ້ງວັດ Patriarchal Stavropegic ຂອງ St. John the Baptist ໃນ Tolleshunt Knights, Maldon, Essex, ອັງກິດ.
Tikhon (Shevkunov): Metropolitan Tikhon ແມ່ນອະທິການຂອງໂບດ Orthodox ລັດເຊຍແລະເປັນນັກຂຽນທີ່ມີຊື່ສຽງ. ລາວແມ່ນເມືອງ Metropolitan ຂອງ Pskov ແລະ Porkhov ແລະໃນປີ 2015–2018 ເປັນຫົວ ໜ້າ ອົງການປົກຄອງຕາເວັນຕົກຂອງນະຄອນມົສກູ ຊັ້ນສູງຂອງອານຸສາວະລີ Sretensky ໃນມອດໂກແຕ່ປີ 1995 ເຖິງປີ 2018. ອະທິການບໍດີ Tikhon ມັກຖືກກ່າວເຖິງວ່າເປັນການສາລະພາບສ່ວນຕົວຂອງປະທານາທິບໍດີລັດເຊຍ Vladimir Putin.
Archimandrite: Archimandrite ຫົວຂໍ້, ໃຊ້ໃນໂບດຄຣິສຕະຈັກຕາເວັນອອກ, ໃນເບື້ອງຕົ້ນໄດ້ກ່າວເຖິງພຣະອາຈານໃຫຍ່ຜູ້ ໜຶ່ງ ທີ່ອະທິການໄດ້ແຕ່ງຕັ້ງໃຫ້ຄວບຄຸມໂບດແລະວັດວາອາຮາມຫຼາຍແຫ່ງ, ຫຼືຕໍ່ພະອາຈານຂອງບາງວັດທີ່ຍິ່ງໃຫຍ່ແລະ ສຳ ຄັນ.
Archimania: archimania ແມ່ນສະຖາປັດຕະຍະ ກຳ ແລະນັກອອກແບບລວມ ໝູ່ ໃນເມືອງ Memphis, ເມືອງສິລະປະປະຫວັດສາດທາງໃຕ້ຂອງ Tennessee. ການລວບລວມໄດ້ຖືກສ້າງຕັ້ງຂຶ້ນໃນປີ 1995 ແລະ ນຳ ພາໂດຍ Todd Walker, FAIA, ແລະ Barry Alan Yoakum, FAIA.
Hierodulinae: The Hierodulinae ແມ່ນ subfamily ຂອງ mantids ອະທິຖານ, ຖືກນໍາໃຊ້ໃນເບື້ອງຕົ້ນໂດຍ Brunner von Wattenwyl. ມັນໄດ້ຖືກຟື້ນຟູຄືນເປັນສ່ວນ ໜຶ່ງ ຂອງການດັດແກ້ທີ່ ສຳ ຄັນຂອງການເກັບພາສີຂອງ mantid, ແລະປະຈຸບັນບັນຈຸ genera ທີ່ຖືກຈັດຢູ່ບ່ອນອື່ນໃນຄອບຄົວ Mantidae.
Archimantis: Archimantis ແມ່ນອະໄວຍະວະຂອງການອະທິຖານທີ່ພົບໃນອົດສະຕາລີ. ຊະນິດພັນເຫຼົ່ານີ້ມີຂະ ໜາດ ຕັ້ງແຕ່ 150 ມມເຖິງ 180 ມມ, ແລະສາມາດຂ້ອນຂ້າງຮຸກຮານເມື່ອເປັນຜູ້ໃຫຍ່ເຕັມທີ່.
Archimantis armata: Archimantis armata ແມ່ນຊະນິດຂອງການອະທິຖານຂອງ mantis ໃນຄອບຄົວ Mantidae.
Archimantis brunneriana: Archimantis brunneriana ແມ່ນຊະນິດຂອງການອະທິຖານໃນຄອບຄົວ Mantidae.
Archimantis gracilis: Archimantis gracilis ແມ່ນຊະນິດຂອງການອະທິຖານຂອງ mantis ໃນຄອບຄົວ Mantidae.
Archimantis latistyla: Archimantis latistyla , ທີ່ຮູ້ກັນທົ່ວໄປວ່ າ mantis ສີນ້ ຳ ຕານຂະ ໜາດ ໃຫຍ່ ແມ່ນຊະນິດຂອງຕົ້ນໄມ້ mantid ຂອງປະເທດອົດສະຕາລີ. The mantis ສີນ້ໍາຕານຂະຫນາດໃຫຍ່ມີສອງ subspecies, ເປັນຍ່ອຍທີ່ກວ້າງຂວາງແລະຜີ mantis ໄມ້ຈາກ Bundabergs Turtle Sands. ຜີທີ່ເປັນຜີບໍ່ແມ່ນຮຸກຮານຄືກັບຊະນິດທີ່ກວ້າງຂວາງແຕ່ມີ ໜ້າ ຈໍປ້ອງກັນທີ່ໃຊ້ເພື່ອເຮັດໃຫ້ mantis ປະກົດຕົວໃຫຍ່ຂື້ນໂດຍການລອກເອົາຂາເບື້ອງ ໜ້າ ລົງທາງອາກາດແລະວາງຫົວຂອງມັນລົງພ້ອມກັບເສົາອາກາດຂອງມັນ. ໂຕແມ່ສີນ້ ຳ ຕານຂະ ໜາດ ໃຫຍ່ແມ່ນສີນ້ ຳ ຕານອ່ອນໆພ້ອມກັບຜູ້ຍິງມີປີກສັ້ນແລະມີປີກຍາວ. ເຄື່ອງຍ່ອຍຈາກ Bundaberg ແມ່ນສີຄີມຈືດໆສີຂາວແລະມີຕາສີເຫຼືອງແລະສີ ດຳ ຢູ່ລະຫວ່າງແຂນ. ແມ່ຍີງສີນ້ ຳ ຕານຂະ ໜາດ ໃຫຍ່ມີປີກສັ້ນ - ປີກຂອງນາງຮອດພຽງແຕ່ເຄິ່ງ ໜຶ່ງ ຂອງທ້ອງຂອງນາງແລະນາງບໍ່ສາມາດບິນໄດ້ - ແຕ່ວ່າຜູ້ຊາຍປີກຍາວມີປີກທີ່ປົກຄຸມທ້ອງທັງ ໝົດ. ພວກມັນມີປີກສອງຄູ່ - ຄູ່ເທິງແມ່ນປີກປົກຄຸມແລະປີກລຸ່ມຊ່ວຍໃຫ້ mantis ບິນໄດ້.
monstrosa Archimantis: Archimantis monstrosa ແມ່ນຊະນິດຂອງ mantid ໃນຄອບຄົວ Mantidae. A. monstrosa , ຫຼື mantis monster, ໂດຍທົ່ວໄປຮອດລວງຍາວ 90 ມມຫຼືຫຼາຍກວ່ານັ້ນ. ມັນເປັນເລື່ອງ ທຳ ມະດາທີ່ບໍ່ຄ່ອຍຈະເຫັນດອກໄມ້ສີນ້ ຳ ຕານຂະ ໜາດ ໃຫຍ່ທີ່ມັກເຫັນ. A. monstrosa ທີ່ອາໄສຢູ່ໃກ້ແຄມຝັ່ງທະເລສາມາດມີ ຈຳ ນວນຫລາຍແລະບາງຄັ້ງກໍ່ຈະໂຈມຕີຜູ້ຖືກລ້າທີ່ໃຫຍ່ກວ່າ.
Archimantis quinquelobata: Archimantis quinquelobata ແມ່ນຊະນິດຂອງການອະທິຖານໃນຄອບຄົວ Mantidae.
Archimantis sobrina: Archimantis sobrina ແມ່ນຊະນິດຂອງການອະທິຖານຂອງ mantis ໃນຄອບຄົວ Mantidae.
Archimantis straminea: Archimantis straminea ແມ່ນຊະນິດຂອງການອະທິຖານໃນຄອບຄົວ Mantidae.
Archimantis vittata: Archimantis vittata ແມ່ນຊະນິດຂອງການອະທິຖານ mantis ໃນຄອບຄົວ Mantidae. ມັນໄດ້ຖືກພົບເຫັນຢູ່ໃນອົດສະຕາລີ.
ArchiMate: ArchiMate ແມ່ນພາສາແບບ ຈຳ ລອງແບບສະຖາປັດຕະຍະ ກຳ ວິສາຫະກິດທີ່ເປີດກວ້າງແລະເປັນເອກະລາດເພື່ອສະ ໜັບ ສະ ໜູນ ຄຳ ອະທິບາຍ, ການວິເຄາະແລະການເບິ່ງເຫັນສະຖາປັດຕະຍະ ກຳ ພາຍໃນແລະທົ່ວໂດເມນທຸລະກິດໃນແບບທີ່ບໍ່ມີຕົວຕົນ
Benno von Archimboldi: Benno von Archimboldi ແມ່ນຕົວລະຄອນປະດິດແຕ່ງໃນນະວະນິຍາຍປີ 2666 (2004) ໂດຍ Roberto Bolaño.
Giuseppe Arcimboldo: Giuseppe Arcimboldo ແມ່ນນັກແຕ້ມຮູບຄົນອີຕາລີທີ່ຮູ້ຈັກດີທີ່ສຸດ ສຳ ລັບການສ້າງຫົວຮູບຄົນທີ່ມີຈິນຕະນາການເຮັດດ້ວຍວັດຖຸຕ່າງໆເຊັ່ນ: ໝາກ ໄມ້, ຜັກ, ດອກໄມ້, ປາແລະປື້ມ.
ສີ່ອົງປະກອບ (Arcimboldo): The Four Elements ແມ່ນຊຸດຮູບແຕ້ມນ້ ຳ ມັນ 4 ແຜ່ນໂດຍນັກສິລະປິນຊາວອີຕາລີ Giuseppe Arcimboldo ເຊິ່ງຖືກສ້າງຂື້ນໃນປີ 1566, ໃນໄລຍະ Renaissance, ສຳ ລັບ Maximilian II, ພະມະຫາກະສັດ Roman Emperor. ຮູບແຕ້ມດັ່ງກ່າວໄດ້ພັນລະນາເຖິງໃບ ໜ້າ ຂອງມະນຸດໃນຮູບປະກອບຂອງຮູບສັດແລະວັດຖຸຕ່າງໆ. ອາກາດ ເປັນຕົວແທນຂອງນົກ, ໄຟ ໂດຍການເຜົາໄມ້ແລະແຄນ, ແຜ່ນດິນໂລກ ໂດຍສັດທີ່ດິນແລະ ນ້ ຳ ໂດຍສັດທະເລ. ຊຸດດັ່ງກ່າວພະຍາຍາມສະແດງການສ້າງຄວາມກົມກຽວຈາກຄວາມວຸ່ນວາຍໂດຍການຈັດວາງສັດປ່າຢ່າງລະມັດລະວັງເພື່ອປະກອບຮູບແຕ້ມໃນຂະນະທີ່ຍັງໄດ້ສັນລະເສີນ Maximilian ໂດຍແນະ ນຳ ວ່າລາວເປັນຜູ້ປົກຄອງທີ່ຄວບຄຸມແມ້ແຕ່ສີ່ອົງປະກອບຕົ້ນສະບັບ.
ບັນຊີລາຍຊື່ຂອງກະເບື້ອງທີ່ເປັນເອກະພາບຂອງ Euclidean: ຕາຕະລາງນີ້ສະແດງໃຫ້ເຫັນເສັ້ນທາງ 11 ຫລ່ຽມທີ່ເປັນເອກະພາບຂອງຍົນ Euclidean, ແລະໂຄ້ງສອງດ້ານຂອງມັນ.
LOL (ເກມວີດີໂອ): LOL , ທີ່ຮູ້ກັນໃນເອີຣົບວ່າ Bakushow ແລະໃນຍີ່ປຸ່ນວ່າ Archime DS , ແມ່ນເກມວີດີໂອ Nintendo DS. ເກມໄດ້ຖືກເຜີຍແຜ່ໂດຍ Skip Ltd ໃນປະເທດຍີ່ປຸ່ນ, Agetec ໃນອາເມລິກາ ເໜືອ, ແລະເກມ Rising Star Games ໃນ Europe.Developed ໂດຍກຸ່ມ ໜຶ່ງ ຄົນ 5 ຄົນທີ່ ນຳ ໂດຍ Kenichi Nishi, LOL ແມ່ນເກມທີ່ມີຄົນຫຼິ້ນຫຼາຍປະຕິບັດດ້ວຍຕົວໂຕ້ຕອບທີ່ຄ້າຍຄື PictoChat ເຊິ່ງ ເຄື່ອງຫຼີ້ນເຈົ້າພາບຖາມ ຄຳ ຖາມ, ຮຽກຮ້ອງໃຫ້ຜູ້ອື່ນຂຽນຫຼືແຕ້ມ ຄຳ ຕອບຂອງພວກເຂົາໃນ ໜ້າ ຈໍ DS touch.
Archimede: Archimede ແມ່ນແບບຟອມ Archimedes ຂອງຝຣັ່ງແລະອິຕາລີ. ມັນອາດຈະອ້າງອີງເຖິງ:
Archimède le clochard: Archimède le clochard ແມ່ນຮູບເງົາລະຄອນຝຣັ່ງປີ 1959 ທີ່ ກຳ ກັບໂດຍ Gilles Grangier. ມັນຍັງມີຊື່ວ່າ The Magnificent Tramp . ຮູບເງົາເລື່ອງນີ້ໄດ້ເຂົ້າໄປໃນງານເທດສະການຮູບເງົາສາກົນເບີລິນຄັ້ງທີ 9, ເຊິ່ງ Jean Gabin ໄດ້ຮັບລາງວັນນັກສະແດງລະຄອນເງິນ.
ເຮືອ ດຳ ນ້ ຳ Archimede-class: ຫ້ອງຮຽນ Archimede ແມ່ນກຸ່ມເຮືອ ດຳ ນ້ ຳ 4 ລຳ ທີ່ສ້າງຂຶ້ນ ສຳ ລັບ Regia Marina ໃນຕົ້ນຊຸມປີ 1930. ເຮືອດັ່ງກ່າວໄດ້ຕໍ່ສູ້ໃນສົງຄາມກາງເມືອງແອສປາໂຍນແລະໃນສົງຄາມໂລກຄັ້ງທີ 2. ພາຍໃຕ້ສີສັນຂອງປະເທດສະເປນ, ເຮືອເຫຼົ່ານີ້ແມ່ນເປັນທີ່ຮູ້ຈັກກັນໃນນາມ General Mola , ແລະຍັງຄົງໃຊ້ບໍລິການຈົນເຖິງປີ 1959.
ເຮືອ ດຳ ນ້ ຳ Italian Archimede (1939): Archimede ແມ່ນເຮືອ ດຳ ນ້ ຳ Brin -class ສ້າງ ສຳ ລັບກອງທັບເຮືອ Royal Italian Navy ໃນຊ່ວງປີ 1930.
Archimede: Archimede ແມ່ນແບບຟອມ Archimedes ຂອງຝຣັ່ງແລະອິຕາລີ. ມັນອາດຈະອ້າງອີງເຖິງ:
Archimede Fusillo: Archimede Fusillo ແມ່ນຜູ້ຂຽນປື້ມຂອງອົດສະຕາລີ ສຳ ລັບເດັກນ້ອຍແລະຜູ້ໃຫຍ່ໄວ ໜຸ່ມ.
Archimede Morleo: Archimede Morleo ແມ່ນນັກກິລາບານເຕະຊາວອິຕາລີຜູ້ທີ່ຫລິ້ນໃຫ້ສະໂມສອນ Eccellenza Apulia Casarano.
Archimede Nardi: Archimede Nardi ແມ່ນນັກເຕະບານມືອາຊີບຂອງອີຕາລີ.
ໂຮງງານໄຟຟ້າຮອບວຽນ Archimede: ໂຮງງານໄຟຟ້າ ປະສົມປະສານ Archimede ແມ່ນ ໂຮງ ງານຜະລິດພະລັງງານຜະລິດພະລັງງານແສງອາທິດລວມ (ISCC) ທີ່ໂຮງງານ Priolo Gargallo ໃກ້ Syracuse ໃນເມືອງ Sicily, ອີຕາລີ ພາກສ່ວນວົງຈອນປະສົມໄດ້ເປີດ ນຳ ໃຊ້ໃນປີ 2003, ແລະພາກສະ ໜາມ ແສງຕາເວັນໃນວັນທີ 14 ກໍລະກົດ 2010. ພາກສະ ໜາມ ແສງຕາເວັນແມ່ນແຫ່ງ ທຳ ອິດທີ່ໃຊ້ເກືອແຮ່ໃນການໂອນຄວາມຮ້ອນແລະການເກັບຮັກສາເຊິ່ງປະສົມປະສານກັບສະຖານທີ່ອາຍແກັສວົງຈອນລວມ. ມັນໃຊ້ເທັກໂນໂລຢີທີ່ພັດທະນາໂດຍ ENEA ແລະ Archimede Solar Energy ເຊິ່ງເປັນການຮ່ວມທຶນລະຫວ່າງ Angelantoni Industrie ແລະ Siemens Energy. Archimede ແມ່ນເປັນເຈົ້າຂອງແລະດໍາເນີນການໂດຍ Enel.
Archimede Vestri: Archimede Vestri (1846–1904) ແມ່ນນັກຮັກຊາດແລະສະຖາປະນິກອີຕາລີ, ເກີດຢູ່ໃນ Siena. ຄຽງຄູ່ກັບພໍ່ຂອງລາວ, Giovanni, ແລະເອື້ອຍຂອງລາວ, Baldovina Vestri, ພວກເຂົາຖືກບັງຄັບໃຫ້ຫນີຈາກ Siena ແລະເຮືອນຂອງພວກເຂົາ, Palazzo Vestri, ໃນປີ 1849. Baldovina ແມ່ນເພື່ອນທີ່ຮູ້ຈັກແລະສະ ໜັບ ສະ ໜູນ Giuseppe Garibaldi.
ເຮືອ ດຳ ນ້ ຳ Archimede-class: ຫ້ອງຮຽນ Archimede ແມ່ນກຸ່ມເຮືອ ດຳ ນ້ ຳ 4 ລຳ ທີ່ສ້າງຂຶ້ນ ສຳ ລັບ Regia Marina ໃນຕົ້ນຊຸມປີ 1930. ເຮືອດັ່ງກ່າວໄດ້ຕໍ່ສູ້ໃນສົງຄາມກາງເມືອງແອສປາໂຍນແລະໃນສົງຄາມໂລກຄັ້ງທີ 2. ພາຍໃຕ້ສີສັນຂອງປະເທດສະເປນ, ເຮືອເຫຼົ່ານີ້ແມ່ນເປັນທີ່ຮູ້ຈັກກັນໃນນາມ General Mola , ແລະຍັງຄົງໃຊ້ບໍລິການຈົນເຖິງປີ 1959.
ໂຮງງານໄຟຟ້າຮອບວຽນ Archimede: ໂຮງງານໄຟຟ້າ ປະສົມປະສານ Archimede ແມ່ນ ໂຮງ ງານຜະລິດພະລັງງານຜະລິດພະລັງງານແສງອາທິດລວມ (ISCC) ທີ່ໂຮງງານ Priolo Gargallo ໃກ້ Syracuse ໃນເມືອງ Sicily, ອີຕາລີ ພາກສ່ວນວົງຈອນປະສົມໄດ້ເປີດ ນຳ ໃຊ້ໃນປີ 2003, ແລະພາກສະ ໜາມ ແສງຕາເວັນໃນວັນທີ 14 ກໍລະກົດ 2010. ພາກສະ ໜາມ ແສງຕາເວັນແມ່ນແຫ່ງ ທຳ ອິດທີ່ໃຊ້ເກືອແຮ່ໃນການໂອນຄວາມຮ້ອນແລະການເກັບຮັກສາເຊິ່ງປະສົມປະສານກັບສະຖານທີ່ອາຍແກັສວົງຈອນລວມ. ມັນໃຊ້ເທັກໂນໂລຢີທີ່ພັດທະນາໂດຍ ENEA ແລະ Archimede Solar Energy ເຊິ່ງເປັນການຮ່ວມທຶນລະຫວ່າງ Angelantoni Industrie ແລະ Siemens Energy. Archimede ແມ່ນເປັນເຈົ້າຂອງແລະດໍາເນີນການໂດຍ Enel.
ລະບົບການກໍ່ສ້າງ Archimede: ລະບົບການກໍ່ສ້າງແບບ Archimede ແມ່ນເຕັກນິກການກໍ່ສ້າງທີ່ບັນລຸຮູບຊົງທີ່ເປັນຮູບຊົງຂອງ rhombic, ເລຂາຄະນິດທີ່ເຕັມໄປດ້ວຍພື້ນທີ່. ໃນອາເມລິກາ, ລະບົບເຫຼົ່ານີ້ສ່ວນໃຫຍ່ສ້າງຊອງຈົດ ໝາຍ ການກໍ່ສ້າງທີ່ປະກອບດ້ວຍຮູບຊົງແລະຂະ ໜາດ ນ້ອຍສອງກະດານ, ຄຸນລັກສະນະນີ້ຊ່ວຍໃຫ້ອຸດສາຫະ ກຳ ສູງສຸດ. ກະດານເຫຼົ່ານີ້ໂດຍທົ່ວໄປແລ້ວແມ່ນຖືກກົດດັນດ້ວຍການໃສ່ທໍ່ລະບາຍຄວາມຮ້ອນທີ່ມີໂຄງສ້າງຄ້າຍຄືກັບໂພລີຍູລີເທນ. ໃນທະວີບເອີຣົບແລະອາຊີ, ໂຄງປະກອບໄປສະນີແລະ beam ມັກສ້າງຮູບຊົງ dodecahedral ເຊິ່ງຫລັງຈາກນັ້ນກໍ່ເຕັມໄປດ້ວຍວັດສະດຸຫຸ້ມຫໍ່ທີ່ແຕກຕ່າງກັນ. ເຖິງແມ່ນວ່າເລຂາຄະນິດຂັ້ນພື້ນຖານບາງຄັ້ງກໍ່ມີເຮືອນທັງ ໝົດ, ແຕ່ລະບົບສ່ວນຫຼາຍແມ່ນລະບົບສັບຊ້ອນຂອງແຕ່ລະຈຸລັງທີ່ປະກອບເປັນພື້ນທີ່ ດຳ ລົງຊີວິດທີ່ມີຮູບຮ່າງຂອງ rhombic ເຊິ່ງສາມາດເປັນຫ້ອງຫລືພື້ນທີ່ ດຳ ລົງຊີວິດທີ່ກວ້າງກວ່າເມື່ອສົມທົບກັບໂມດູນ dodecahedral ທີ່ຢູ່ຕິດກັນ.
Archimède le clochard: Archimède le clochard ແມ່ນຮູບເງົາລະຄອນຝຣັ່ງປີ 1959 ທີ່ ກຳ ກັບໂດຍ Gilles Grangier. ມັນຍັງມີຊື່ວ່າ The Magnificent Tramp . ຮູບເງົາເລື່ອງນີ້ໄດ້ເຂົ້າໄປໃນງານເທດສະການຮູບເງົາສາກົນເບີລິນຄັ້ງທີ 9, ເຊິ່ງ Jean Gabin ໄດ້ຮັບລາງວັນນັກສະແດງລະຄອນເງິນ.
ໂຮງງານໄຟຟ້າຮອບວຽນ Archimede: ໂຮງງານໄຟຟ້າ ປະສົມປະສານ Archimede ແມ່ນ ໂຮງ ງານຜະລິດພະລັງງານຜະລິດພະລັງງານແສງອາທິດລວມ (ISCC) ທີ່ໂຮງງານ Priolo Gargallo ໃກ້ Syracuse ໃນເມືອງ Sicily, ອີຕາລີ ພາກສ່ວນວົງຈອນປະສົມໄດ້ເປີດ ນຳ ໃຊ້ໃນປີ 2003, ແລະພາກສະ ໜາມ ແສງຕາເວັນໃນວັນທີ 14 ກໍລະກົດ 2010. ພາກສະ ໜາມ ແສງຕາເວັນແມ່ນແຫ່ງ ທຳ ອິດທີ່ໃຊ້ເກືອແຮ່ໃນການໂອນຄວາມຮ້ອນແລະການເກັບຮັກສາເຊິ່ງປະສົມປະສານກັບສະຖານທີ່ອາຍແກັສວົງຈອນລວມ. ມັນໃຊ້ເທັກໂນໂລຢີທີ່ພັດທະນາໂດຍ ENEA ແລະ Archimede Solar Energy ເຊິ່ງເປັນການຮ່ວມທຶນລະຫວ່າງ Angelantoni Industrie ແລະ Siemens Energy. Archimede ແມ່ນເປັນເຈົ້າຂອງແລະດໍາເນີນການໂດຍ Enel.
Archimedean: ວິທີ Archimedean ໝາຍ ເຖິງຫຼືກ່ຽວຂ້ອງກັບຫລືທີ່ມີຊື່ໃນກຽດສັກສີຂອງນັກຄະນິດສາດຊາວເກຣັກ Archimedes ແລະອາດຈະອ້າງເຖິງ:
Archimedean: ວິທີ Archimedean ໝາຍ ເຖິງຫຼືກ່ຽວຂ້ອງກັບຫລືທີ່ມີຊື່ໃນກຽດສັກສີຂອງນັກຄະນິດສາດຊາວເກຣັກ Archimedes ແລະອາດຈະອ້າງເຖິງ:
ລາຊະວົງ Archimedean: Archimedean Dynasty ແມ່ນຄັ້ງ ທຳ ອິດຂອງເກມຄອມພິວເຕີ້ AquaNox , ຖືກພັດທະນາໂດຍ Massive Development ແລະຖືກພີມໂດຍ Blue Byte ໃນປີ 1996. ໃນວັນທີ 29 ກໍລະກົດ 2015, ຫຼັງຈາກທີ່ບໍ່ສາມາດໃຊ້ໄດ້ຫຼາຍປີ, ເກມໄດ້ຖືກປ່ອຍອອກມາ ໃໝ່ ໃນ gog ຕົວແທນ ຈຳ ໜ່າຍ ດິຈິຕອນ. com ກັບການສະຫນັບສະຫນູນ Windows.
ຄວາມຕື່ນເຕັ້ນ Archimedean: Archimedean Excogitation ແມ່ນຮູບປັ້ນບານລວດລາຍປີ 1987 ໂດຍ George Rhoads. ມັນຕັ້ງຢູ່ໃນ atrium ຂອງພິພິທະພັນວິທະຍາສາດໃນ Boston.
ຈຸດ Archimedean: ຈຸດ Archimedean ແມ່ນມຸມມອງທີ່ສົມມຸດຖານເຊິ່ງຄວາມຈິງຈຸດປະສົງສະເພາະໃດ ໜຶ່ງ ສາມາດເຂົ້າໃຈໄດ້ຢ່າງສົມບູນຫຼືເປັນຈຸດເລີ່ມຕົ້ນທີ່ ໜ້າ ເຊື່ອຖືຈາກການທີ່ຄົນ ໜຶ່ງ ສາມາດຫາເຫດຜົນ. ເວົ້າອີກຢ່າງ ໜຶ່ງ, ມຸມມອງຈາກຈຸດ Archimedean ອະທິບາຍເຖິງຄວາມ ເໝາະ ສົມຂອງການເອົາຕົວເອງອອກຈາກຈຸດປະສົງຂອງການສຶກສາເພື່ອໃຫ້ຄົນ ໜຶ່ງ ສາມາດເຫັນມັນກ່ຽວຂ້ອງກັບສິ່ງອື່ນໆທັງ ໝົດ ໃນຂະນະທີ່ຍັງມີຄວາມເປັນເອກະລາດ.
Archimedean Oath: The Archimedean Oath ແມ່ນລະຫັດການປະຕິບັດດ້ານຈັນຍາບັນ ສຳ ລັບວິສະວະກອນແລະນັກວິຊາການ, ຄ້າຍຄືກັບ Hippocratic Oath ໃຊ້ໃນໂລກທາງການແພດ ມັນໄດ້ຖືກສະເຫນີໃນປີ 1990 ໂດຍກຸ່ມນັກຮຽນຂອງ thecole polytechnique fédérale de Lausanne. ຕັ້ງແຕ່ນັ້ນມາ, Archimedean Oath ໄດ້ແຜ່ລາມໄປໂຮງຮຽນວິສະວະ ກຳ ເອີຣົບ ຈຳ ນວນ ໜຶ່ງ.
ຈຸດ Archimedean: ຈຸດ Archimedean ແມ່ນມຸມມອງທີ່ສົມມຸດຖານເຊິ່ງຄວາມຈິງຈຸດປະສົງສະເພາະໃດ ໜຶ່ງ ສາມາດເຂົ້າໃຈໄດ້ຢ່າງສົມບູນຫຼືເປັນຈຸດເລີ່ມຕົ້ນທີ່ ໜ້າ ເຊື່ອຖືຈາກການທີ່ຄົນ ໜຶ່ງ ສາມາດຫາເຫດຜົນ. ເວົ້າອີກຢ່າງ ໜຶ່ງ, ມຸມມອງຈາກຈຸດ Archimedean ອະທິບາຍເຖິງຄວາມ ເໝາະ ສົມຂອງການເອົາຕົວເອງອອກຈາກຈຸດປະສົງຂອງການສຶກສາເພື່ອໃຫ້ຄົນ ໜຶ່ງ ສາມາດເຫັນມັນກ່ຽວຂ້ອງກັບສິ່ງອື່ນໆທັງ ໝົດ ໃນຂະນະທີ່ຍັງມີຄວາມເປັນເອກະລາດ.
ສະກູ Archimedes: ສະ ກູ Archimedes , ເຊິ່ງເອີ້ນກັນວ່າສະ ກູລະບາຍນ້ ຳ , ຈັກສູບ ນ້ ຳ ສະກູ ຫລືສະ ກູຂອງອີຢິບ , ແມ່ນເຄື່ອງຈັກທີ່ໃຊ້ ສຳ ລັບໂອນນ້ ຳ ຈາກຮ່າງກາຍຂອງນ້ ຳ ທີ່ຕ່ ຳ ລົງສູ່ຄອງຊົນລະປະທານ. ນໍ້າໄດ້ຖືກຈັກສູບໂດຍການປ່ຽນ ໜ້າ ດິນທີ່ມີຮູບຮ່າງ screw ພາຍໃນທໍ່. ມັນຖືກຕັ້ງຊື່ຕາມນັກປັດຊະຍາຊາວເກຣັກ Archimedes ຜູ້ທີ່ໄດ້ບັນຍາຍມັນຄັ້ງ ທຳ ອິດປະມານ 234 ປີກ່ອນຄ. ສ. ເຄື່ອງເຈາະສະກູແມ່ນອຸປະກອນທີ່ຄ້າຍຄືກັນທີ່ສົ່ງວັດສະດຸສ່ວນໃຫຍ່ເຊັ່ນແປ້ງແລະເມັດພືດ.
Archimedean ແຂງ: ໃນທາງເລຂາຄະນິດ, ທາດແຂງ Archimedean ແມ່ນ ໜຶ່ງ ໃນ 13 ທາດແຂງທີ່ໄດ້ລວບລວມຂໍ້ມູນໂດຍ Archimedes. ພວກມັນແມ່ນ polyhedra ທີ່ເປັນເອກະພາບທີ່ມີຄວາມສົມດູນປະກອບດ້ວຍການປະຊຸມ polygons ປົກກະຕິໃນແນວຕັ້ງທີ່ຄ້າຍຄືກັນ, ບໍ່ລວມເອົາທາດລະລາຍທັງ 5 Platonic ແລະບໍ່ລວມເອົາພວງມະລາຍແລະສັດຕູພືດ. ພວກມັນແຕກຕ່າງຈາກຈຸດແຂງຂອງ Johnson, ເຊິ່ງໃບ ໜ້າ polygonal ປົກກະຕິບໍ່ໄດ້ພົບກັນໃນແນວຕັ້ງທີ່ຄ້າຍຄືກັນ.
Archimedean ແຂງ: ໃນທາງເລຂາຄະນິດ, ທາດແຂງ Archimedean ແມ່ນ ໜຶ່ງ ໃນ 13 ທາດແຂງທີ່ໄດ້ລວບລວມຂໍ້ມູນໂດຍ Archimedes. ພວກມັນແມ່ນ polyhedra ທີ່ເປັນເອກະພາບທີ່ມີຄວາມສົມດູນປະກອບດ້ວຍການປະຊຸມ polygons ປົກກະຕິໃນແນວຕັ້ງທີ່ຄ້າຍຄືກັນ, ບໍ່ລວມເອົາທາດລະລາຍທັງ 5 Platonic ແລະບໍ່ລວມເອົາພວງມະລາຍແລະສັດຕູພືດ. ພວກມັນແຕກຕ່າງຈາກຈຸດແຂງຂອງ Johnson, ເຊິ່ງໃບ ໜ້າ polygonal ປົກກະຕິບໍ່ໄດ້ພົບກັນໃນແນວຕັ້ງທີ່ຄ້າຍຄືກັນ.
ກ້ຽວວຽນ Archimedean: ກ້ຽວວຽນ Archimedean ແມ່ນກ້ຽວວຽນທີ່ມີຊື່ຕາມສະກຸນ Archimedes ນັກຄະນິດສາດເຣັກໃນສະຕະວັດທີ 3 BC ມັນແມ່ນສະຖານທີ່ທີ່ສອດຄ້ອງກັບສະຖານທີ່ຕ່າງໆຕາມການເວລາຂອງຈຸດທີ່ຍ້າຍອອກໄປຈາກຈຸດຄົງທີ່ທີ່ມີຄວາມໄວຄົງທີ່ຕາມເສັ້ນທີ່ ໝຸນ ກັບຄວາມໄວຂອງມຸມ. ຢ່າງເທົ່າທຽມກັນ, ໃນການປະສານງານຂົ້ວໂລກ ( r , θ ) ມັນສາມາດຖືກອະທິບາຍໂດຍສົມຜົນ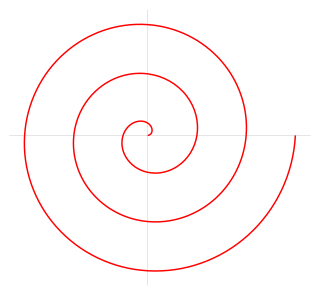
Conservatory Upper Archimedean: Archimedean Upper Conservatory ແມ່ນໂຮງຮຽນມັດທະຍົມສາທາລະນະໃນ Miami, Florida. Archimedean Upper Conservatory (AUC) ແມ່ນສະມາຊິກຂອງໂຮງຮຽນ Archimedean. ໂຮງຮຽນ Archimedean ແມ່ນໂຮງຮຽນ K-12 ທີ່ໄດ້ຮັບການຄຸ້ມຄອງແບບເປັນອິດສະຫຼະໂດຍຜ່ານລະບົບໂຮງຮຽນສາທາລະນະ 12 ແຫ່ງທີ່ສ້າງຕັ້ງຂື້ນໃນປີ 2002 ໂດຍບໍລິສັດ Archimedean Academy Inc. ໂຮງຮຽນ Archimedean ປະກອບມີສາມສູນການອະນຸລັກທີ່ເຮັດວຽກສູງສຸມໃສ່ວິຊາຄະນິດສາດແລະພາສາກະເຣັກ: Archimedean Academy, Archimedean Middle Conservatory, ທັງສອງແຫ່ງຊາດໄດ້ຮັບຮູ້ວ່າເປັນໂຮງຮຽນ Blue Ribbon 2011, ແລະ 2012 AdvancED SACS-CASI Accredited Archimedean Upper Conservatory. ໂຮງຮຽນ Archimedean ແມ່ນເຂດອະນຸລັກຂອງຄະນິດສາດແລະພາສາກະເຣັກ. ຫຼັກສູດທີ່ໄດ້ຮັບການປັບປຸງຂອງພວກເຂົາສຸມໃສ່ໃນຄວາມເລິກໃນ: ຄະນິດສາດທີ່ກ້າວ ໜ້າ ໃນພາສາອັງກິດແລະພາສາກະເຣັກ, ວິທະຍາສາດທີ່ກ້າວ ໜ້າ (7-12) ໂຄງການ" ຟີຊິກ ທຳ ອິດ", ແລະປັດຊະຍາ ສຳ ລັບເດັກ (6-12) ທີ່ມີຫົວຂໍ້ແລະແນວຄິດທີ່ເລືອກໃນດ້ານຈັນຍາບັນ, ການປຽບທຽບແລະເຫດຜົນ. ການຮັບໃຊ້ນັກຮຽນຫຼາຍພາສາຫຼາຍວັດທະນະ ທຳ, ຫຼາຍພາສາ 1,140 ແຫ່ງ, ໂຮງຮຽນ Archimedean ໄດ້ຈັດອັນດັບຢ່າງຖືກຕ້ອງໃນບັນດາໂຮງຮຽນລັດແລະເອກະຊົນທີ່ມີຜົນງານສູງສຸດໃນເຂດປົກຄອງ, ລັດ Florida ແລະປະເທດຊາດ. ຖະແຫຼງການພາລະກິດຂອງໂຮງຮຽນແມ່ນ `` ເພື່ອເລີ່ມຕົ້ນຈິດໃຈໄວ ໜຸ່ມ ໃນສິລະປະການຄິດໂດຍຜ່ານການສອນຄະນິດສາດແລະພາສາກະເຣັກ.
ມູນຄ່າຢ່າງແທ້ຈິງ (ພຶດຊະຄະນິດ): ໃນພຶດຊະຄະນິດ, ຄຸນຄ່າຢ່າງແທ້ຈິງ ແມ່ນ ໜ້າ ທີ່ທີ່ວັດແທກ "ຂະ ໜາດ" ຂອງອົງປະກອບໃນສະ ໜາມ ຫຼືໂດເມນລວມ. ທີ່ຊັດເຈນກວ່ານັ້ນ, ຖ້າ D ແມ່ນໂດເມນລວມ, ຫຼັງຈາກນັ້ນ ມູນຄ່າທີ່ແທ້ຈິງ ແມ່ນແຜນທີ່ | x | ຈາກ D ເຖິງຕົວເລກຕົວຈິງ R ພໍໃຈ:
ຊັບສິນ Archimedean: ໃນຄະນິດສາດແລະບົດວິເຄາະທີ່ບໍ່ມີຕົວຕົນ, ຊັບສິນ Archimedean , ຕັ້ງຊື່ຕາມຊື່ຄະນິດສາດດ້ານວັດຖຸບູຮານ Archimedes ຂອງ Syracuse, ແມ່ນຊັບສິນທີ່ຖືໂດຍໂຄງສ້າງພຶຊະຄະນິດ ຈຳ ນວນ ໜຶ່ງ, ເຊັ່ນ: ກຸ່ມທີ່ມີ ຄຳ ສັ່ງຫຼືມີມາດຕະຖານ, ແລະທົ່ງນາ. ຄຸນສົມບັດດັ່ງກ່າວຖືກສ້າງຂື້ນໂດຍປົກກະຕິລະບຸວ່າໃຫ້ສອງຕົວເລກ x ແລະ y , ມັນມີເລກເຕັມ n ເພື່ອວ່າ nx > y . ມັນຍັງ ໝາຍ ຄວາມວ່າຊຸດຕົວເລກ ທຳ ມະຊາດບໍ່ໄດ້ຖືກຜູກຢູ່ຂ້າງເທິງ. ເວົ້າໂດຍຫຍໍ້, ມັນແມ່ນຊັບສົມບັດຂອງການບໍ່ມີອົງປະກອບ ນ້ອຍ ຫລື ໃຫຍ່ທີ່ ບໍ່ມີຂອບເຂດ . ມັນແມ່ນ Otto Stolz ຜູ້ທີ່ໃຫ້ຊື່ຂອງ Archimedes ຍ້ອນວ່າມັນປະກົດວ່າເປັນ Axiom V ຂອງ Archimedes ' On the Sphere ແລະກະບອກ .
Archimedean ແຂງ: ໃນທາງເລຂາຄະນິດ, ທາດແຂງ Archimedean ແມ່ນ ໜຶ່ງ ໃນ 13 ທາດແຂງທີ່ໄດ້ລວບລວມຂໍ້ມູນໂດຍ Archimedes. ພວກມັນແມ່ນ polyhedra ທີ່ເປັນເອກະພາບທີ່ມີຄວາມສົມດູນປະກອບດ້ວຍການປະຊຸມ polygons ປົກກະຕິໃນແນວຕັ້ງທີ່ຄ້າຍຄືກັນ, ບໍ່ລວມເອົາທາດລະລາຍທັງ 5 Platonic ແລະບໍ່ລວມເອົາພວງມະລາຍແລະສັດຕູພືດ. ພວກມັນແຕກຕ່າງຈາກຈຸດແຂງຂອງ Johnson, ເຊິ່ງໃບ ໜ້າ polygonal ປົກກະຕິບໍ່ໄດ້ພົບກັນໃນແນວຕັ້ງທີ່ຄ້າຍຄືກັນ.
Archimedean ແຂງ: ໃນທາງເລຂາຄະນິດ, ທາດແຂງ Archimedean ແມ່ນ ໜຶ່ງ ໃນ 13 ທາດແຂງທີ່ໄດ້ລວບລວມຂໍ້ມູນໂດຍ Archimedes. ພວກມັນແມ່ນ polyhedra ທີ່ເປັນເອກະພາບທີ່ມີຄວາມສົມດູນປະກອບດ້ວຍການປະຊຸມ polygons ປົກກະຕິໃນແນວຕັ້ງທີ່ຄ້າຍຄືກັນ, ບໍ່ລວມເອົາທາດລະລາຍທັງ 5 Platonic ແລະບໍ່ລວມເອົາພວງມະລາຍແລະສັດຕູພືດ. ພວກມັນແຕກຕ່າງຈາກຈຸດແຂງຂອງ Johnson, ເຊິ່ງໃບ ໜ້າ polygonal ປົກກະຕິບໍ່ໄດ້ພົບກັນໃນແນວຕັ້ງທີ່ຄ້າຍຄືກັນ.
ຮູບວົງມົນ Archimedean: ໃນຮູບເລຂາຄະນິດ, ຮູບວົງມົນ Archimedean ແມ່ນ ຮູບວົງມົນ ໃດ ໜຶ່ງ ທີ່ສ້າງຈາກ arbelos ເຊິ່ງມີລັດສະ ໝີ ຄືກັນກັບແຕ່ລະວົງແຫວນຄູ່ແຝດ Archimedes. ຖ້າ arbelos ໄດ້ຮັບມາດຕະຖານເຊັ່ນວ່າເສັ້ນຜ່າກາງຂອງວົງກົມເຄິ່ງກາງ (ໃຫຍ່ທີ່ສຸດ) ຂອງມັນມີຄວາມຍາວ 1 ແລະ r ໝາຍ ເຖິງ radiius ຂອງວົງມົນເຄິ່ງ ໜຶ່ງ ຂອງວົງແຫວນພາຍໃນ, ຫຼັງຈາກນັ້ນລັດສະ ໝີ ρ ຂອງວົງວຽນ Archimedean ດັ່ງກ່າວແມ່ນໃຫ້ໂດຍ
ສີທີ່ເປັນເອກະພາບ: ໃນດ້ານເລຂາຄະນິດ, ສີທີ່ເປັນເອກະພາບ ແມ່ນຄຸນສົມບັດຂອງຕົວເລກທີ່ເປັນເອກະພາບທີ່ມີສີສັນໃຫ້ເປັນຮູບແບບ vertex-transitive. ຕົວຊີ້ວັດທີ່ແຕກຕ່າງກັນສາມາດສະແດງອອກໃນຕົວເລກເລຂາຄະນິດດຽວກັນກັບໃບ ໜ້າ ປະຕິບັດຕາມຮູບແບບສີທີ່ແຕກຕ່າງກັນ.
Pi: ໝາຍ ເລກ π ແມ່ນເລກຄະນິດສາດຄົງທີ່. ມັນຖືກ ກຳ ນົດເປັນອັດຕາສ່ວນຂອງວົງກົມຂອງວົງກົມກັບເສັ້ນຜ່າສູນກາງຂອງມັນ, ແລະມັນຍັງມີ ຄຳ ນິຍາມທຽບເທົ່າກັນ. ມັນປະກົດຢູ່ໃນຫຼາຍສູດໃນທຸກຂົງເຂດຂອງຄະນິດສາດແລະຟີຊິກ. ການນໍາໃຊ້ເປັນທີ່ຮູ້ຈັກທໍາອິດຂອງπຈົດຫມາຍສະບັບກເຣັກເປັນຕົວແທນຂອງອັດຕາສ່ວນຂອງ circumference ວົງຂອງເສັ້ນຜ່າສູນກາງຂອງຕົນແມ່ນ by ແວວນັກຄະນິດສາດ William Jones ໃນ 1706. ມັນແມ່ນປະມານເທົ່າທຽມກັນທີ່ 3,14159. ມັນໄດ້ຖືກສະແດງໂດຍຕົວອັກສອນກະເຣັກ " π " ຕັ້ງແຕ່ກາງສະຕະວັດທີ 18, ແລະຖືກສະກົດອອກເປັນ " pi ". ມັນຍັງຖືກເອີ້ນວ່າຄົງທີ່ຂອງ Archimedes .
Copula (ທິດສະດີຄວາມເປັນໄປໄດ້): ໃນທິດສະດີແລະສະຖິຕິຄວາມເປັນໄປໄດ້, copula ແມ່ນ ໜ້າ ທີ່ການແຈກຢາຍ multivariate ສຳ ລັບການແຈກຢາຍຄວາມເປັນໄປໄດ້ຂອງຂອບຂອງແຕ່ລະຕົວແປທີ່ເປັນເອກະພາບໃນໄລຍະຫ່າງ [0, 1]. Copulas ຖືກ ນຳ ໃຊ້ເພື່ອອະທິບາຍ / ສ້າງແບບ ຈຳ ລອງການເພິ່ງພາອາໄສ (inter-correlation) ລະຫວ່າງຕົວປ່ຽນແບບສຸ່ມ. ຊື່ຂອງພວກເຂົາ, ຖືກ ນຳ ສະ ເໜີ ໂດຍນັກຄະນິດສາດ Abe Sklar ທີ່ ນຳ ໃຊ້ໃນປີ 1959, ແມ່ນມາຈາກພາສາລາຕິນ ສຳ ລັບ "ການເຊື່ອມໂຍງ" ຫຼື "ສາຍ", ຄ້າຍຄືກັນແຕ່ບໍ່ກ່ຽວຂ້ອງກັບຄູຝີມືດ້ານພາສາສາດ Copulas ໄດ້ຖືກ ນຳ ໃຊ້ຢ່າງກວ້າງຂວາງໃນດ້ານການເງິນດ້ານປະລິມານເພື່ອສ້າງແບບ ຈຳ ລອງແລະຫຼຸດຜ່ອນຄວາມສ່ຽງຂອງຫາງແລະການ ນຳ ໃຊ້ໂປແກຼມການເພີ່ມປະສິດທິພາບດ້ານການຄ້າ.
ແຂງກາຕາ: ໃນຄະນິດສາດ, ພາສາກາຕາລັງແຂງ , ຫຼື Archimedean dual , ແມ່ນ polyhedron ຄູ່ກັບ Archimedean ແຂງ. ມີດິນດ່ຽວ 13 ກາຕາ. ພວກມັນຖືກຕັ້ງຊື່ໃຫ້ເປັນນັກຄະນິດສາດຊາວເບລຢ້ຽນຊື່Eugène Catalan, ຜູ້ທີ່ອະທິບາຍພວກມັນໃນປີ 1865
ທິດສະດີ Hahn ທີ່ຝັງໄວ້: ໃນວິຊາຄະນິດສາດ - ໂດຍສະເພາະໃນຂົງເຂດຂອງພຶດຊະຄະນິດພຶດຊະຄະນິດທີ່ກ່ຽວຂ້ອງກັບໂຄງສ້າງທີ່ຖືກສັ່ງໃນກຸ່ມ abelian - ທິດສະດີການຝັງ Hahn ໃຫ້ ຄຳ ອະທິບາຍງ່າຍໆກ່ຽວກັບກຸ່ມ abelian ທີ່ຖືກຈັດລຽງຕາມເສັ້ນ. ມັນຖືກຕັ້ງຊື່ຕາມຊື່ Hans Hahn.
ຊັບສິນ Archimedean: ໃນຄະນິດສາດແລະບົດວິເຄາະທີ່ບໍ່ມີຕົວຕົນ, ຊັບສິນ Archimedean , ຕັ້ງຊື່ຕາມຊື່ຄະນິດສາດດ້ານວັດຖຸບູຮານ Archimedes ຂອງ Syracuse, ແມ່ນຊັບສິນທີ່ຖືໂດຍໂຄງສ້າງພຶຊະຄະນິດ ຈຳ ນວນ ໜຶ່ງ, ເຊັ່ນ: ກຸ່ມທີ່ມີ ຄຳ ສັ່ງຫຼືມີມາດຕະຖານ, ແລະທົ່ງນາ. ຄຸນສົມບັດດັ່ງກ່າວຖືກສ້າງຂື້ນໂດຍປົກກະຕິລະບຸວ່າໃຫ້ສອງຕົວເລກ x ແລະ y , ມັນມີເລກເຕັມ n ເພື່ອວ່າ nx > y . ມັນຍັງ ໝາຍ ຄວາມວ່າຊຸດຕົວເລກ ທຳ ມະຊາດບໍ່ໄດ້ຖືກຜູກຢູ່ຂ້າງເທິງ. ເວົ້າໂດຍຫຍໍ້, ມັນແມ່ນຊັບສົມບັດຂອງການບໍ່ມີອົງປະກອບ ນ້ອຍ ຫລື ໃຫຍ່ທີ່ ບໍ່ມີຂອບເຂດ . ມັນແມ່ນ Otto Stolz ຜູ້ທີ່ໃຫ້ຊື່ຂອງ Archimedes ຍ້ອນວ່າມັນປະກົດວ່າເປັນ Axiom V ຂອງ Archimedes ' On the Sphere ແລະກະບອກ .
ເສັ້ນສະແດງ Archimedean: ໃນຂົງເຂດຄະນິດສາດຂອງທິດສະດີກາຟິກ, ກາຟິກ Archimedean ແມ່ນເສັ້ນສະແດງທີ່ປະກອບເປັນໂຄງກະດູກຂອງ ໜຶ່ງ ໃນບັນດາທາດແຂງ Archimedean. ມີກາຟິກ Archimedean ມີ 13 ເສັ້ນ, ແລະທັງ ໝົດ ແມ່ນກາບກອນປົກກະຕິ, ເປັນໂພສະນາການ, ແລະຍັງມີກາຟ Hamiltonian.
ກຸ່ມ Archimedean: ໃນຄະນິດສາດທີ່ບໍ່ມີຕົວຕົນ, ສາຂາຂອງຄະນິດສາດ, ກຸ່ມ Archimedean ແມ່ນ ກຸ່ມທີ່ ມີໃບສັ່ງຊື້ແບບເສັ້ນທີ່ຊັບສິນ Archimedean ຖື: ທຸກໆສອງອົງປະກອບຂອງກຸ່ມບວກແມ່ນຖືກຜູກມັດດ້ວຍຕົວຄູນຂອງແຕ່ລະຄົນ. ຊຸດ R ຂອງ ຈຳ ນວນຕົວຈິງພ້ອມກັບການ ດຳ ເນີນງານຂອງການເພີ່ມແລະການພົວພັນຕາມ ລຳ ດັບຕາມປົກກະຕິລະຫວ່າງຄູ່ຂອງ ຈຳ ນວນແມ່ນກຸ່ມ Archimedean. ໂດຍຜົນຂອງ Otto Hölder, ທຸກໆກຸ່ມ Archimedean ແມ່ນ isomorphic ກັບກຸ່ມຍ່ອຍຂອງກຸ່ມນີ້. ຊື່ "Archimedean" ແມ່ນມາຈາກ Otto Stolz, ຜູ້ທີ່ຕັ້ງຊື່ຊັບສິນ Archimedean ຫຼັງຈາກທີ່ມີລັກສະນະດັ່ງກ່າວໃນຜົນງານຂອງ Archimedes.
ໂຄນຮັງເຜີ້ງເປັນເອກະພາບ: ໃນດ້ານເລຂາຄະນິດ, ຮັງເຜີ້ງທີ່ເປັນເອກະພາບ ແມ່ນການທົດແທນທີ່ເປັນເອກະພາບເຊິ່ງເຕັມໄປດ້ວຍພື້ນທີ່ Euclidean ສາມມິຕິທີ່ມີຈຸລັງໂພໂລຫະເອກະພາບທີ່ບໍ່ຊ້ ຳ ຊ້ອນກັນ.
ບັນຊີລາຍຊື່ຂອງກະເບື້ອງທີ່ເປັນເອກະພາບຂອງ Euclidean: ຕາຕະລາງນີ້ສະແດງໃຫ້ເຫັນເສັ້ນທາງ 11 ຫລ່ຽມທີ່ເປັນເອກະພາບຂອງຍົນ Euclidean, ແລະໂຄ້ງສອງດ້ານຂອງມັນ.
ກຸ່ມ Archimedean: ໃນຄະນິດສາດທີ່ບໍ່ມີຕົວຕົນ, ສາຂາຂອງຄະນິດສາດ, ກຸ່ມ Archimedean ແມ່ນ ກຸ່ມທີ່ ມີໃບສັ່ງຊື້ແບບເສັ້ນທີ່ຊັບສິນ Archimedean ຖື: ທຸກໆສອງອົງປະກອບຂອງກຸ່ມບວກແມ່ນຖືກຜູກມັດດ້ວຍຕົວຄູນຂອງແຕ່ລະຄົນ. ຊຸດ R ຂອງ ຈຳ ນວນຕົວຈິງພ້ອມກັບການ ດຳ ເນີນງານຂອງການເພີ່ມແລະການພົວພັນຕາມ ລຳ ດັບຕາມປົກກະຕິລະຫວ່າງຄູ່ຂອງ ຈຳ ນວນແມ່ນກຸ່ມ Archimedean. ໂດຍຜົນຂອງ Otto Hölder, ທຸກໆກຸ່ມ Archimedean ແມ່ນ isomorphic ກັບກຸ່ມຍ່ອຍຂອງກຸ່ມນີ້. ຊື່ "Archimedean" ແມ່ນມາຈາກ Otto Stolz, ຜູ້ທີ່ຕັ້ງຊື່ຊັບສິນ Archimedean ຫຼັງຈາກທີ່ມີລັກສະນະດັ່ງກ່າວໃນຜົນງານຂອງ Archimedes.
Archimedean ສັ່ງຊ່ອງ vector: ໃນຄະນິດສາດ, ໂດຍສະເພາະໃນທິດສະດີຕາມ ລຳ ດັບ, ຄວາມ ສຳ ພັນຄູ່ ໃນຊ່ອງ vector ໃນໄລຍະຕົວເລກທີ່ແທ້ຈິງຫຼືສັບຊ້ອນຖືກເອີ້ນວ່າ Archimedean ຖ້າ ສຳ ລັບທຸກຄົນ ເມື່ອໃດກໍ່ຕາມມີບາງ ດັ່ງ​ນັ້ນ ສຳ ລັບເລກເຕັມໃນທາງບວກ ຫຼັງຈາກນັ້ນຈໍາເປັນ Archimedean (ທາງສ່ວນຫນ້າຂອງ) ຄໍາສັ່ງ vector vector ແມ່ນ ພື້ນທີ່ vector ທີ່ສັ່ງ (ກ່ອນ) ທີ່ມີຄໍາສັ່ງແມ່ນ Archimedean. ຊ່ອງ vector ທີ່ຢູ່ເບື້ອງຕົ້ນ ເອີ້ນວ່າ ເກືອບ Archimedean ຖ້າ ສຳ ລັບທຸກຄົນ ເມື່ອໃດກໍ່ຕາມທີ່ມີຢູ່ ດັ່ງ​ນັ້ນ ສຳ ລັບເລກເຕັມໃນທາງບວກ ແລ້ວ
Archimedean ສັ່ງຊ່ອງ vector: ໃນຄະນິດສາດ, ໂດຍສະເພາະໃນທິດສະດີຕາມ ລຳ ດັບ, ຄວາມ ສຳ ພັນຄູ່ ໃນຊ່ອງ vector ໃນໄລຍະຕົວເລກທີ່ແທ້ຈິງຫຼືສັບຊ້ອນຖືກເອີ້ນວ່າ Archimedean ຖ້າ ສຳ ລັບທຸກຄົນ ເມື່ອໃດກໍ່ຕາມມີບາງ ດັ່ງ​ນັ້ນ ສຳ ລັບເລກເຕັມໃນທາງບວກ ຫຼັງຈາກນັ້ນຈໍາເປັນ Archimedean (ທາງສ່ວນຫນ້າຂອງ) ຄໍາສັ່ງ vector vector ແມ່ນ ພື້ນທີ່ vector ທີ່ສັ່ງ (ກ່ອນ) ທີ່ມີຄໍາສັ່ງແມ່ນ Archimedean. ຊ່ອງ vector ທີ່ຢູ່ເບື້ອງຕົ້ນ ເອີ້ນວ່າ ເກືອບ Archimedean ຖ້າ ສຳ ລັບທຸກຄົນ ເມື່ອໃດກໍ່ຕາມທີ່ມີຢູ່ ດັ່ງ​ນັ້ນ ສຳ ລັບເລກເຕັມໃນທາງບວກ ແລ້ວ
ຊັບສິນ Archimedean: ໃນຄະນິດສາດແລະບົດວິເຄາະທີ່ບໍ່ມີຕົວຕົນ, ຊັບສິນ Archimedean , ຕັ້ງຊື່ຕາມຊື່ຄະນິດສາດດ້ານວັດຖຸບູຮານ Archimedes ຂອງ Syracuse, ແມ່ນຊັບສິນທີ່ຖືໂດຍໂຄງສ້າງພຶຊະຄະນິດ ຈຳ ນວນ ໜຶ່ງ, ເຊັ່ນ: ກຸ່ມທີ່ມີ ຄຳ ສັ່ງຫຼືມີມາດຕະຖານ, ແລະທົ່ງນາ. ຄຸນສົມບັດດັ່ງກ່າວຖືກສ້າງຂື້ນໂດຍປົກກະຕິລະບຸວ່າໃຫ້ສອງຕົວເລກ x ແລະ y , ມັນມີເລກເຕັມ n ເພື່ອວ່າ nx > y . ມັນຍັງ ໝາຍ ຄວາມວ່າຊຸດຕົວເລກ ທຳ ມະຊາດບໍ່ໄດ້ຖືກຜູກຢູ່ຂ້າງເທິງ. ເວົ້າໂດຍຫຍໍ້, ມັນແມ່ນຊັບສົມບັດຂອງການບໍ່ມີອົງປະກອບ ນ້ອຍ ຫລື ໃຫຍ່ທີ່ ບໍ່ມີຂອບເຂດ . ມັນແມ່ນ Otto Stolz ຜູ້ທີ່ໃຫ້ຊື່ຂອງ Archimedes ຍ້ອນວ່າມັນປະກົດວ່າເປັນ Axiom V ຂອງ Archimedes ' On the Sphere ແລະກະບອກ .
Archimedean ສັ່ງຊ່ອງ vector: ໃນຄະນິດສາດ, ໂດຍສະເພາະໃນທິດສະດີຕາມ ລຳ ດັບ, ຄວາມ ສຳ ພັນຄູ່ ໃນຊ່ອງ vector ໃນໄລຍະຕົວເລກທີ່ແທ້ຈິງຫຼືສັບຊ້ອນຖືກເອີ້ນວ່າ Archimedean ຖ້າ ສຳ ລັບທຸກຄົນ ເມື່ອໃດກໍ່ຕາມມີບາງ ດັ່ງ​ນັ້ນ ສຳ ລັບເລກເຕັມໃນທາງບວກ ຫຼັງຈາກນັ້ນຈໍາເປັນ Archimedean (ທາງສ່ວນຫນ້າຂອງ) ຄໍາສັ່ງ vector vector ແມ່ນ ພື້ນທີ່ vector ທີ່ສັ່ງ (ກ່ອນ) ທີ່ມີຄໍາສັ່ງແມ່ນ Archimedean. ຊ່ອງ vector ທີ່ຢູ່ເບື້ອງຕົ້ນ ເອີ້ນວ່າ ເກືອບ Archimedean ຖ້າ ສຳ ລັບທຸກຄົນ ເມື່ອໃດກໍ່ຕາມທີ່ມີຢູ່ ດັ່ງ​ນັ້ນ ສຳ ລັບເລກເຕັມໃນທາງບວກ ແລ້ວ
ທິດສະດີເລກ Algebraic: ທິດສະດີເລກ Algebraic ແມ່ນສາຂາຂອງທິດສະດີເລກທີ່ ນຳ ໃຊ້ເຕັກນິກຂອງພຶດຊະຄະນິດພຶດຊະຄະນິດເພື່ອສຶກສາເລກເຕັມ, ຕົວເລກທີ່ສົມເຫດສົມຜົນແລະການ ນຳ ໃຊ້ທົ່ວໄປ. ຄຳ ຖາມທິດສະດີກ່ຽວກັບຕົວເລກແມ່ນສະແດງເຖິງຄຸນລັກສະນະຂອງວັດຖຸພຶດຊະຄະນິດເຊັ່ນ: ທົ່ງນາເລກຄະນິດສາດແລະວົງແຫວນຂອງຕົວເລກ, ຂົງເຂດທີ່ ຈຳ ກັດ, ແລະຂົງເຂດການເຮັດວຽກ. ຄຸນສົມບັດເຫຼົ່ານີ້, ເຊັ່ນວ່າວົງແຫວນໃດ ໜຶ່ງ ຍອມຮັບປັດໄຈທີ່ເປັນເອກະລັກ, ພຶດຕິ ກຳ ຂອງອຸດົມການ, ແລະກຸ່ມ Galois ຂອງຂົງເຂດສາມາດແກ້ໄຂ ຄຳ ຖາມທີ່ມີຄວາມ ສຳ ຄັນຕົ້ນຕໍໃນທິດສະດີ ຈຳ ນວນ, ເຊັ່ນວ່າການມີວິທີແກ້ໄຂໃຫ້ສົມຜົນຂອງ Diophantine.
ຈຸດ Archimedean: ຈຸດ Archimedean ແມ່ນມຸມມອງທີ່ສົມມຸດຖານເຊິ່ງຄວາມຈິງຈຸດປະສົງສະເພາະໃດ ໜຶ່ງ ສາມາດເຂົ້າໃຈໄດ້ຢ່າງສົມບູນຫຼືເປັນຈຸດເລີ່ມຕົ້ນທີ່ ໜ້າ ເຊື່ອຖືຈາກການທີ່ຄົນ ໜຶ່ງ ສາມາດຫາເຫດຜົນ. ເວົ້າອີກຢ່າງ ໜຶ່ງ, ມຸມມອງຈາກຈຸດ Archimedean ອະທິບາຍເຖິງຄວາມ ເໝາະ ສົມຂອງການເອົາຕົວເອງອອກຈາກຈຸດປະສົງຂອງການສຶກສາເພື່ອໃຫ້ຄົນ ໜຶ່ງ ສາມາດເຫັນມັນກ່ຽວຂ້ອງກັບສິ່ງອື່ນໆທັງ ໝົດ ໃນຂະນະທີ່ຍັງມີຄວາມເປັນເອກະລາດ.