Archimedean solid, Archimedean principle, Archimedean property

Archimedean ແຂງ: ໃນທາງເລຂາຄະນິດ, ທາດແຂງ Archimedean ແມ່ນ ໜຶ່ງ ໃນ 13 ທາດແຂງທີ່ໄດ້ລວບລວມໂດຍ Archimedes. ພວກມັນແມ່ນ polyhedra ທີ່ເປັນເອກະພາບປະສົມປະສານຂອງການປະຊຸມ polygons ປົກກະຕິໃນແນວຕັ້ງທີ່ຄ້າຍຄືກັນ, ບໍ່ລວມເອົາທາດລະລາຍທັງ 5 Platonic ແລະບໍ່ລວມເອົາພວງມະລາຍແລະປ້ອງກັນພະຍາດ. ພວກມັນແຕກຕ່າງຈາກຈຸດແຂງຂອງ Johnson, ເຊິ່ງໃບ ໜ້າ polygonal ປົກກະຕິບໍ່ໄດ້ພົບກັນໃນແນວຕັ້ງທີ່ຄ້າຍຄືກັນ.
ຫຼັກການ Archimedean: ຫຼັກການ Archimedean ອາດຈະອີງໃສ່: ຫຼັກການຂອງ Archimedes, ເຊິ່ງເປັນຫຼັກການທີ່ກ່ຽວຂ້ອງກັບການໄຫຼວຽນຂອງການຍ້າຍຖິ່ນຖານ ຊັບສິນ Archimedean, ຊັບສິນທາງຄະນິດສາດຂອງຕົວເລກແລະໂຄງສ້າງພຶດຊະຄະນິດອື່ນໆ
ຊັບສິນ Archimedean: ໃນຄະນິດສາດແລະການວິເຄາະທີ່ບໍ່ມີຕົວຕົນ, ຊັບສິນ Archimedean , ທີ່ຕັ້ງຊື່ຕາມຊື່ຄະນິດສາດຊັ້ນສູງຂອງເກຼັກ Archimedes of Syracuse, ແມ່ນຊັບສິນທີ່ຖືກຈັດຂື້ນໂດຍໂຄງສ້າງກ່ຽວກັບພຶດຊະຄະນິດບາງຢ່າງ, ເຊັ່ນ: ກຸ່ມທີ່ມີ ຄຳ ສັ່ງຫຼືມາດຕະຖານ, ແລະທົ່ງນາ. ຄຸນສົມບັດ, ທີ່ຖືກສ້າງຂື້ນໂດຍປົກກະຕິລະບຸວ່າໃຫ້ສອງຕົວເລກ x ແລະ y , ມັນຈະມີເລກເຕັມ n ເພື່ອວ່າ nx > y . ມັນຍັງຫມາຍຄວາມວ່າຊຸດຂອງຕົວເລກທໍາມະຊາດບໍ່ໄດ້ຖືກຜູກຢູ່ຂ້າງເທິງ. ເວົ້າໂດຍຫຍໍ້, ມັນແມ່ນຊັບສົມບັດຂອງການບໍ່ມີອົງປະກອບ ນ້ອຍ ຫລື ໃຫຍ່ທີ່ ບໍ່ມີຂອບເຂດ . ມັນແມ່ນ Otto Stolz ຜູ້ທີ່ໃຫ້ຊື່ຂອງ Archimedes ຍ້ອນວ່າມັນປະກົດວ່າເປັນ Axiom V ຂອງ Archimedes ' On the Sphere ແລະກະບອກ .
ຊັບສິນ Archimedean: ໃນຄະນິດສາດແລະການວິເຄາະທີ່ບໍ່ມີຕົວຕົນ, ຊັບສິນ Archimedean , ທີ່ຕັ້ງຊື່ຕາມຊື່ຄະນິດສາດຊັ້ນສູງຂອງເກຼັກ Archimedes of Syracuse, ແມ່ນຊັບສິນທີ່ຖືກຈັດຂື້ນໂດຍໂຄງສ້າງກ່ຽວກັບພຶດຊະຄະນິດບາງຢ່າງ, ເຊັ່ນ: ກຸ່ມທີ່ມີ ຄຳ ສັ່ງຫຼືມາດຕະຖານ, ແລະທົ່ງນາ. ຄຸນສົມບັດ, ທີ່ຖືກສ້າງຂື້ນໂດຍປົກກະຕິລະບຸວ່າໃຫ້ສອງຕົວເລກ x ແລະ y , ມັນຈະມີເລກເຕັມ n ເພື່ອວ່າ nx > y . ມັນຍັງຫມາຍຄວາມວ່າຊຸດຂອງຕົວເລກທໍາມະຊາດບໍ່ໄດ້ຖືກຜູກຢູ່ຂ້າງເທິງ. ເວົ້າໂດຍຫຍໍ້, ມັນແມ່ນຊັບສົມບັດຂອງການບໍ່ມີອົງປະກອບ ນ້ອຍ ຫລື ໃຫຍ່ທີ່ ບໍ່ມີຂອບເຂດ . ມັນແມ່ນ Otto Stolz ຜູ້ທີ່ໃຫ້ຊື່ຂອງ Archimedes ຍ້ອນວ່າມັນປະກົດວ່າເປັນ Axiom V ຂອງ Archimedes ' On the Sphere ແລະກະບອກ .
ສະກູ Archimedes: ສະ ກູຂອງ Archimedes , ເຊິ່ງເອີ້ນກັນວ່າສະ ກູລະບາຍນ້ ຳ , ຈັກສູບ ນ້ ຳ ສະກູ ຫລືສະ ກູຂອງອີຢິບ , ແມ່ນເຄື່ອງຈັກທີ່ໃຊ້ ສຳ ລັບໂອນນ້ ຳ ຈາກຮ່າງກາຍຂອງນ້ ຳ ທີ່ຕ່ ຳ ລົງສູ່ຄອງຊົນລະປະທານ. ນໍ້າໄດ້ຖືກຈັກສູບໂດຍການຫັນ ໜ້າ ດິນທີ່ມີຮູບຮ່າງ screw ພາຍໃນທໍ່. ມັນຖືກຕັ້ງຊື່ຕາມນັກປັດຊະຍາຊາວເກຣັກ Archimedes ຜູ້ທີ່ໄດ້ບັນຍາຍມັນຄັ້ງ ທຳ ອິດປະມານ 234 ປີກ່ອນຄ. ສ. ເຄື່ອງເຈາະສະກູແມ່ນອຸປະກອນທີ່ຄ້າຍຄືກັນທີ່ສົ່ງວັດສະດຸສ່ວນໃຫຍ່ເຊັ່ນແປ້ງແລະເມັດພືດ.
ຊັບສິນ Archimedean: ໃນຄະນິດສາດແລະການວິເຄາະທີ່ບໍ່ມີຕົວຕົນ, ຊັບສິນ Archimedean , ທີ່ຕັ້ງຊື່ຕາມຊື່ຄະນິດສາດຊັ້ນສູງຂອງເກຼັກ Archimedes of Syracuse, ແມ່ນຊັບສິນທີ່ຖືກຈັດຂື້ນໂດຍໂຄງສ້າງກ່ຽວກັບພຶດຊະຄະນິດບາງຢ່າງ, ເຊັ່ນ: ກຸ່ມທີ່ມີ ຄຳ ສັ່ງຫຼືມາດຕະຖານ, ແລະທົ່ງນາ. ຄຸນສົມບັດ, ທີ່ຖືກສ້າງຂື້ນໂດຍປົກກະຕິລະບຸວ່າໃຫ້ສອງຕົວເລກ x ແລະ y , ມັນຈະມີເລກເຕັມ n ເພື່ອວ່າ nx > y . ມັນຍັງຫມາຍຄວາມວ່າຊຸດຂອງຕົວເລກທໍາມະຊາດບໍ່ໄດ້ຖືກຜູກຢູ່ຂ້າງເທິງ. ເວົ້າໂດຍຫຍໍ້, ມັນແມ່ນຊັບສົມບັດຂອງການບໍ່ມີອົງປະກອບ ນ້ອຍ ຫລື ໃຫຍ່ທີ່ ບໍ່ມີຂອບເຂດ . ມັນແມ່ນ Otto Stolz ຜູ້ທີ່ໃຫ້ຊື່ຂອງ Archimedes ຍ້ອນວ່າມັນປະກົດວ່າເປັນ Axiom V ຂອງ Archimedes ' On the Sphere ແລະກະບອກ .
ຊັບສິນ Archimedean: ໃນຄະນິດສາດແລະການວິເຄາະທີ່ບໍ່ມີຕົວຕົນ, ຊັບສິນ Archimedean , ທີ່ຕັ້ງຊື່ຕາມຊື່ຄະນິດສາດຊັ້ນສູງຂອງເກຼັກ Archimedes of Syracuse, ແມ່ນຊັບສິນທີ່ຖືກຈັດຂື້ນໂດຍໂຄງສ້າງກ່ຽວກັບພຶດຊະຄະນິດບາງຢ່າງ, ເຊັ່ນ: ກຸ່ມທີ່ມີ ຄຳ ສັ່ງຫຼືມາດຕະຖານ, ແລະທົ່ງນາ. ຄຸນສົມບັດ, ທີ່ຖືກສ້າງຂື້ນໂດຍປົກກະຕິລະບຸວ່າໃຫ້ສອງຕົວເລກ x ແລະ y , ມັນຈະມີເລກເຕັມ n ເພື່ອວ່າ nx > y . ມັນຍັງຫມາຍຄວາມວ່າຊຸດຂອງຕົວເລກທໍາມະຊາດບໍ່ໄດ້ຖືກຜູກຢູ່ຂ້າງເທິງ. ເວົ້າໂດຍຫຍໍ້, ມັນແມ່ນຊັບສົມບັດຂອງການບໍ່ມີອົງປະກອບ ນ້ອຍ ຫລື ໃຫຍ່ທີ່ ບໍ່ມີຂອບເຂດ . ມັນແມ່ນ Otto Stolz ຜູ້ທີ່ໃຫ້ຊື່ຂອງ Archimedes ຍ້ອນວ່າມັນປະກົດວ່າເປັນ Axiom V ຂອງ Archimedes ' On the Sphere ແລະກະບອກ .
Archimedean ແຂງ: ໃນທາງເລຂາຄະນິດ, ທາດແຂງ Archimedean ແມ່ນ ໜຶ່ງ ໃນ 13 ທາດແຂງທີ່ໄດ້ລວບລວມໂດຍ Archimedes. ພວກມັນແມ່ນ polyhedra ທີ່ເປັນເອກະພາບປະສົມປະສານຂອງການປະຊຸມ polygons ປົກກະຕິໃນແນວຕັ້ງທີ່ຄ້າຍຄືກັນ, ບໍ່ລວມເອົາທາດລະລາຍທັງ 5 Platonic ແລະບໍ່ລວມເອົາພວງມະລາຍແລະປ້ອງກັນພະຍາດ. ພວກມັນແຕກຕ່າງຈາກຈຸດແຂງຂອງ Johnson, ເຊິ່ງໃບ ໜ້າ polygonal ປົກກະຕິບໍ່ໄດ້ພົບກັນໃນແນວຕັ້ງທີ່ຄ້າຍຄືກັນ.
Archimedean ແຂງ: ໃນທາງເລຂາຄະນິດ, ທາດແຂງ Archimedean ແມ່ນ ໜຶ່ງ ໃນ 13 ທາດແຂງທີ່ໄດ້ລວບລວມໂດຍ Archimedes. ພວກມັນແມ່ນ polyhedra ທີ່ເປັນເອກະພາບປະສົມປະສານຂອງການປະຊຸມ polygons ປົກກະຕິໃນແນວຕັ້ງທີ່ຄ້າຍຄືກັນ, ບໍ່ລວມເອົາທາດລະລາຍທັງ 5 Platonic ແລະບໍ່ລວມເອົາພວງມະລາຍແລະປ້ອງກັນພະຍາດ. ພວກມັນແຕກຕ່າງຈາກຈຸດແຂງຂອງ Johnson, ເຊິ່ງໃບ ໜ້າ polygonal ປົກກະຕິບໍ່ໄດ້ພົບກັນໃນແນວຕັ້ງທີ່ຄ້າຍຄືກັນ.
ກ້ຽວວຽນ Archimedean: ກ້ຽວວຽນ Archimedean ແມ່ນກ້ຽວວຽນທີ່ມີຊື່ຕາມສະກຸນ Archimedes ນັກຄະນິດສາດເຣັກໃນສະຕະວັດທີ 3 ກ່ອນຄ. ສ. ມັນແມ່ນສະຖານທີ່ທີ່ສອດຄ້ອງກັບສະຖານທີ່ຕ່າງໆຕາມການເວລາຂອງຈຸດທີ່ຍ້າຍອອກໄປຈາກຈຸດຄົງທີ່ທີ່ມີຄວາມໄວຄົງທີ່ຕາມເສັ້ນທີ່ ໝຸນ ກັບຄວາມໄວຂອງມຸມ. ເທົ່າທຽມກັນ, ໃນການປະສານງານຂົ້ວໂລກ ( r , θ ) ມັນສາມາດອະທິບາຍໄດ້ໂດຍສົມຜົນ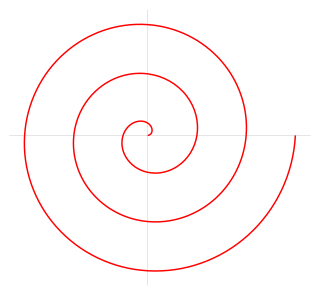
ກະເບື້ອງ Euclidean ໂດຍ convex polygons ປົກກະຕິ: ການ ຍັບຍັ້ງການ ບິນຂອງຍົນ Euclidean ໂດຍ polycons ປົກກະຕິ ໄດ້ຖືກ ນຳ ໃຊ້ຢ່າງກວ້າງຂວາງຕັ້ງແຕ່ສະ ໄໝ ເກົ່າ ການ ບຳ ບັດທາງຄະນິດສາດທີ່ເປັນລະບົບ ທຳ ອິດແມ່ນຂອງ Kepler ໃນ Harmonices Mundi ຂອງລາວ.
ວິທີການຂອງທິດສະດີກົນຈັກ: ວິທີການກ່ຽວກັບທິດສະດີກົນຈັກ , ຍັງຖືກເອີ້ນວ່າ The Method , ຖືວ່າເປັນ ໜຶ່ງ ໃນບັນດາຜົນງານທີ່ມີຊີວິດລອດທີ່ ສຳ ຄັນຂອງ Polymath Archimedes ຂອງກເຣັກໂບຮານ. ວິທີໃຊ້ເວລາຮູບແບບຂອງຈົດຫມາຍສະບັບຈາກ Archimedes ກັບ Eratosthenes, ຫ້ອງສະຫມຸດຫົວຫນ້າຢູ່ຫໍສະຫມຸດຂອງ Alexandria ໄດ້, ແລະປະກອບດ້ວຍທໍາອິດ attested ໃຊ້ຢ່າງຊັດເຈນຂອງຕັດແຍກອອກ. ວຽກງານດັ່ງກ່າວໄດ້ຖືກຄິດໃນເບື້ອງຕົ້ນວ່າຈະຫາຍໄປ, ແຕ່ໃນປີ 1906 ໄດ້ຖືກຄົ້ນພົບຄືນ ໃໝ່ ໃນງານສະເຫຼີມສະຫຼອງ Archimedes Palimpsest. palimpsest ປະກອບມີບັນຊີຂອງ Archimedes ກ່ຽວກັບ "ວິທີການກົນຈັກ", ດັ່ງນັ້ນເອີ້ນວ່າຍ້ອນວ່າມັນອີງໃສ່ກົດຫມາຍຂອງ lever, ເຊິ່ງໄດ້ຖືກສະແດງໃຫ້ເຫັນຄັ້ງທໍາອິດໂດຍ Archimedes, ແລະສູນກາງຂອງມະຫາຊົນ, ເຊິ່ງລາວໄດ້ພົບເຫັນຫລາຍຮູບແບບພິເສດ.
ມູນຄ່າຢ່າງແທ້ຈິງ (ພຶດຊະຄະນິດ): ໃນພຶດຊະຄະນິດ, ຄຸນຄ່າຢ່າງແທ້ຈິງ ແມ່ນ ໜ້າ ທີ່ທີ່ວັດແທກ "ຂະ ໜາດ" ຂອງອົງປະກອບໃນສະ ໜາມ ຫຼືໂດເມນລວມ. ທີ່ຊັດເຈນກວ່ານັ້ນ, ຖ້າ D ແມ່ນໂດເມນລວມ, ຫຼັງຈາກນັ້ນ ມູນຄ່າຢ່າງແທ້ຈິງ ແມ່ນແຜນທີ່ | x | ຈາກ D ເຖິງຕົວເລກຕົວຈິງ R ພໍໃຈ:
The Archimedeans: Archimedeans ແມ່ນສັງຄົມຄະນິດສາດຂອງມະຫາວິທະຍາໄລ Cambridge, ສ້າງຕັ້ງຂຶ້ນໃນປີ 1935. ປະຈຸບັນມີສະມາຊິກທີ່ມີການເຄື່ອນໄຫວຫຼາຍກວ່າ 2000 ຄົນ, ເຊິ່ງຫຼາຍຄົນແມ່ນນັກສຶກສາເກົ່າ, ເຮັດໃຫ້ມັນກາຍເປັນ ໜຶ່ງ ໃນສັງຄົມນັກຮຽນທີ່ໃຫຍ່ທີ່ສຸດໃນ Cambridge. ສັງຄົມຈັດການໂອ້ລົມເປັນປະ ຈຳ ຢູ່ສູນວິທະຍາສາດຄະນິດສາດ, ລວມທັງໃນອະດີດໂດຍນັກເວົ້າທີ່ມີຊື່ສຽງໃນພາກວິຊາຄະນິດສາດ. ມັນເຜີຍແຜ່ວາລະສານສອງສະບັບຄື Eureka ແລະ QARCH .
Archimedes: Archimedes of Syracuse ແມ່ນນັກຄະນິດສາດ, ນັກຟີຊິກ, ວິສະວະກອນ, ນັກປະດິດ, ແລະນັກດາລາສາດ. ເຖິງວ່າຈະມີລາຍລະອຽດ ໜ້ອຍ ໜຶ່ງ ກ່ຽວກັບຊີວິດຂອງລາວ, ແຕ່ລາວຖືວ່າເປັນ ໜຶ່ງ ໃນນັກວິທະຍາສາດຊັ້ນ ນຳ ໃນສະ ໄໝ ເກົ່າແກ່. ຖືວ່າເປັນນັກຄະນິດສາດທີ່ຍິ່ງໃຫຍ່ທີ່ສຸດໃນປະຫວັດສາດບູຮານ, ແລະ ໜຶ່ງ ໃນສິ່ງທີ່ຍິ່ງໃຫຍ່ທີ່ສຸດໃນທຸກເວລາ, Archimedes ໄດ້ຄາດຄະເນການຄິດໄລ່ແລະການວິເຄາະທີ່ທັນສະ ໄໝ ໂດຍການ ນຳ ໃຊ້ແນວຄວາມຄິດຂອງຂະ ໜາດ ນ້ອຍແລະວິທີການ ໝົດ ແຮງເພື່ອເອົາມາໃຊ້ແລະພິສູດຢ່າງເລິກເຊິ່ງກ່ຽວກັບທິດສະດີທິດສະດີທາງເລຂາຄະນິດ, ລວມທັງ : ພື້ນທີ່ຂອງວົງມົນ; ພື້ນທີ່ແລະບໍລິມາດຂອງພື້ນທີ່; ເນື້ອທີ່ຂອງຮູບໄຂ່; ພື້ນທີ່ພາຍໃຕ້ parabola ເປັນ; ປະລິມານຂອງສ່ວນຂອງ paraboloid ຂອງການປະຕິວັດ; ປະລິມານຂອງສ່ວນຂອງ hyperboloid ຂອງການປະຕິວັດ; ແລະພື້ນທີ່ຂອງກ້ຽວວຽນ.
ບັນຫາການລ້ຽງສັດຂອງ Archimedes: ບັນຫາການລ້ຽງສັດຂອງ Archimedes ແມ່ນເປັນປັນຫາໃນການວິເຄາະ Diophantine, ການສຶກສາສົມຜົນຂອງ polynomial ກັບວິທີແກ້ໄຂແບບເຕັມ. ເນື່ອງຈາກ Archimedes, ບັນຫາກ່ຽວຂ້ອງກັບການຄິດໄລ່ ຈຳ ນວນງົວໃນຝູງສັດພະເຈົ້າແສງຕາເວັນຈາກຂໍ້ ຈຳ ກັດທີ່ ກຳ ນົດໄວ້. ບັນຫາດັ່ງກ່າວຖືກຄົ້ນພົບໂດຍ Gotthold Ephraim Lessing ໃນ ໜັງ ສືໃບລານກເຣັກບັນຈຸບົດກະວີຂອງສີ່ສິບສີ່ເສັ້ນ, ໃນຫໍສະ ໝຸດ Herzog August ໃນWolfenbüttel, ປະເທດເຢຍລະມັນໃນປີ 1773.
ບັນຫາການລ້ຽງສັດຂອງ Archimedes: ບັນຫາການລ້ຽງສັດຂອງ Archimedes ແມ່ນເປັນປັນຫາໃນການວິເຄາະ Diophantine, ການສຶກສາສົມຜົນຂອງ polynomial ກັບວິທີແກ້ໄຂແບບເຕັມ. ເນື່ອງຈາກ Archimedes, ບັນຫາກ່ຽວຂ້ອງກັບການຄິດໄລ່ ຈຳ ນວນງົວໃນຝູງສັດພະເຈົ້າແສງຕາເວັນຈາກຂໍ້ ຈຳ ກັດທີ່ ກຳ ນົດໄວ້. ບັນຫາດັ່ງກ່າວຖືກຄົ້ນພົບໂດຍ Gotthold Ephraim Lessing ໃນ ໜັງ ສືໃບລານກເຣັກບັນຈຸບົດກະວີຂອງສີ່ສິບສີ່ເສັ້ນ, ໃນຫໍສະ ໝຸດ Herzog August ໃນWolfenbüttel, ປະເທດເຢຍລະມັນໃນປີ 1773.
ຮອຍທພບຂອງ Archimedes: ຮອຍທພບຂອງ Archimedes ແມ່ນອາວຸດວັດຖຸບູຮານທີ່ຖືກສ້າງຂື້ນໂດຍ Archimedes ເພື່ອປ້ອງກັນສ່ວນທະເລຂອງ ກຳ ແພງເມືອງ Syracuse ຕໍ່ຕ້ານການບຸກໂຈມຕີທີ່ສວຍງາມ. ເຖິງແມ່ນວ່າລັກສະນະທີ່ແນ່ນອນຂອງມັນຍັງບໍ່ຈະແຈ້ງ, ບັນຊີຂອງນັກປະຫວັດສາດບູຮານເບິ່ງຄືວ່າພັນລະນາເຖິງວ່າມັນເປັນແບບຊະນິດຂອງເຄນທີ່ຕິດກັບເຄື່ອງເຈາະທີ່ສາມາດຍົກເຮືອໂຈມຕີໄດ້ສ່ວນ ໜຶ່ງ ອອກຈາກນ້ ຳ, ຈາກນັ້ນກໍ່ອາດຈະເຮັດໃຫ້ເຮືອດັ່ງກ່າວຕົກລົງຫຼືຕົກລົງຢ່າງກະທັນຫັນ ມັນ. ມັນຖືກຖິ້ມລົງໃສ່ເຮືອສັດຕູ, ເຊິ່ງຫຼັງຈາກນັ້ນກໍ່ຈະແກວ່ງຕົວເອງແລະ ທຳ ລາຍ ກຳ ປັ່ນ.
Pi: ໝາຍ ເລກ π ແມ່ນເລກຄະນິດສາດຄົງທີ່. ມັນຖືກ ກຳ ນົດເປັນອັດຕາສ່ວນຂອງວົງກົມຂອງວົງກົມກັບເສັ້ນຜ່າສູນກາງຂອງມັນ, ແລະມັນຍັງມີ ຄຳ ນິຍາມທຽບເທົ່າກັນ. ມັນປະກົດຢູ່ໃນຫຼາຍສູດໃນທຸກຂົງເຂດຂອງຄະນິດສາດແລະຟີຊິກ. ການນໍາໃຊ້ເປັນທີ່ຮູ້ຈັກທໍາອິດຂອງπຈົດຫມາຍສະບັບກເຣັກເປັນຕົວແທນຂອງອັດຕາສ່ວນຂອງ circumference ວົງຂອງເສັ້ນຜ່າສູນກາງຂອງຕົນແມ່ນ by ແວວນັກຄະນິດສາດ William Jones ໃນ 1706. ມັນແມ່ນປະມານເທົ່າທຽມກັນທີ່ 3,14159. ມັນໄດ້ຖືກສະແດງໂດຍຕົວອັກສອນກະເຣັກ " π " ຕັ້ງແຕ່ກາງສະຕະວັດທີ 18, ແລະຖືກສະກົດອອກເປັນ " pi ". ມັນຍັງຖືກເອີ້ນວ່າຄົງທີ່ຂອງ Archimedes .
ຢູ່ໃນຂອບເຂດແລະທໍ່ກົມ: ໃນ Sphere ແລະ Cylinder ແມ່ນວຽກງານ ໜຶ່ງ ທີ່ຖືກຕີພິມໂດຍ Archimedes ເປັນສອງເຫຼັ້ມ c. 225 ສ. ສ. ມັນມີລາຍລະອຽດພິເສດທີ່ສຸດກ່ຽວກັບວິທີການຄົ້ນຫາພື້ນທີ່ຂອງຂອບແລະປະລິມານຂອງບານທີ່ບັນຈຸແລະຄ່າທີ່ຄ້າຍຄືກັນ ສຳ ລັບກະບອກ, ແລະເປັນຜູ້ ທຳ ອິດທີ່ເຮັດເຊັ່ນນັ້ນ.
ໝາຍ ເລກ Archimedes: ໃນນະໂຍບາຍດ້ານນ້ ຳ viscous, ຈຳ ນວນ Archimedes ( Ar ), ແມ່ນ ຈຳ ນວນມິຕິທີ່ໃຊ້ໃນການ ກຳ ນົດການເຄື່ອນໄຫວຂອງທາດແຫຼວຍ້ອນຄວາມແຕກຕ່າງຄວາມ ໜາ ແໜ້ນ, ຕັ້ງຊື່ຕາມນັກວິທະຍາສາດແລະນັກຄະນິດສາດຊາວເກຼັກບູຮານ Archimedes.
Archimedes Palimpsest: The Archimedes Palimpsest ແມ່ນ parchment codex palimpsest, ໃນເບື້ອງຕົ້ນແມ່ນ ສຳ ເນົາ Byzantine Greek ຂອງການລວບລວມຂອງ Archimedes ແລະຜູ້ຂຽນອື່ນໆ. ທຸກໆຮູບພາບແລະຂໍ້ມູນຈາກການບັນທຶກສາມາດໃຊ້ໄດ້ໃນອິນເຕີເນັດທີ່ Archimedes Digital Palimpsest, ພາຍໃຕ້ Creative Commons License CC BY.
ການປ່ຽນແປງຂອງແຮງດັນແບບແນວຕັ້ງ: ການປ່ຽນແປງຂອງຄວາມກົດດັນແບບແນວຕັ້ງ ແມ່ນການປ່ຽນແປງຂອງຄວາມກົດດັນທີ່ເປັນ ໜ້າ ທີ່ຂອງການສູງ. ອີງຕາມທາດແຫຼວໃນ ຄຳ ຖາມແລະສະພາບການທີ່ຖືກກ່າວເຖິງ, ມັນອາດຈະມີຄວາມແຕກຕ່າງກັນຢ່າງຫຼວງຫຼາຍໃນແຕ່ລະດ້ານຕາມລວງກວ້າງເຊັ່ນດຽວກັນ, ແລະການປ່ຽນແປງເຫຼົ່ານີ້ມີຄວາມກ່ຽວຂ້ອງໃນສະພາບການຂອງແຮງກົດດັນແລະຜົນກະທົບຂອງມັນ. ເຖິງຢ່າງໃດກໍ່ຕາມ, ການປ່ຽນແປງທາງແນວຕັ້ງແມ່ນມີຄວາມ ສຳ ຄັນເປັນພິເສດ, ຍ້ອນວ່າມັນເປັນຜົນມາຈາກການດຶງແຮງໂນ້ມຖ່ວງໃສ່ທາດແຫຼວ; ຄືກັນກັບ ສຳ ລັບນ້ ຳ ທີ່ໃຫ້ໃນລະດັບດຽວກັນ, ການຫຼຸດລົງຂອງລະດັບຄວາມສູງພາຍໃນມັນເທົ່າກັບຖັນທີ່ສູງກວ່າຂອງນ້ ຳ ໜັກ ທີ່ມີນ້ ຳ ໜັກ ລົງໃນຈຸດນັ້ນ.
ຫຼັກການຂອງ Archimedes: ຫລັກການຂອງ Archimedes ລະ ບຸວ່າແຮງກະຕຸ້ນທີ່ຂຶ້ນໄປເທິງທີ່ຖືກປ່ອຍອອກຈາກຮ່າງກາຍທີ່ຖືກຈຸ່ມລົງໃນນໍ້າ, ບໍ່ວ່າຈະເຕັມຫຼືບາງສ່ວນ, ເທົ່າກັບນ້ ຳ ໜັກ ຂອງທາດແຫຼວທີ່ຮ່າງກາຍຍ້າຍອອກ. ຫຼັກການຂອງ Archimedes ແມ່ນກົດ ໝາຍ ຂອງຟີຊິກພື້ນຖານຕໍ່ກັບກົນຈັກນ້ ຳ. ມັນຖືກສ້າງຂື້ນໂດຍ Archimedes of Syracuse.
ສະກູ Archimedes: ສະ ກູຂອງ Archimedes , ເຊິ່ງເອີ້ນກັນວ່າສະ ກູລະບາຍນ້ ຳ , ຈັກສູບ ນ້ ຳ ສະກູ ຫລືສະ ກູຂອງອີຢິບ , ແມ່ນເຄື່ອງຈັກທີ່ໃຊ້ ສຳ ລັບໂອນນ້ ຳ ຈາກຮ່າງກາຍຂອງນ້ ຳ ທີ່ຕ່ ຳ ລົງສູ່ຄອງຊົນລະປະທານ. ນໍ້າໄດ້ຖືກຈັກສູບໂດຍການຫັນ ໜ້າ ດິນທີ່ມີຮູບຮ່າງ screw ພາຍໃນທໍ່. ມັນຖືກຕັ້ງຊື່ຕາມນັກປັດຊະຍາຊາວເກຣັກ Archimedes ຜູ້ທີ່ໄດ້ບັນຍາຍມັນຄັ້ງ ທຳ ອິດປະມານ 234 ປີກ່ອນຄ. ສ. ເຄື່ອງເຈາະສະກູແມ່ນອຸປະກອນທີ່ຄ້າຍຄືກັນທີ່ສົ່ງວັດສະດຸສ່ວນໃຫຍ່ເຊັ່ນແປ້ງແລະເມັດພືດ.
Ostomachion: Ostomachion , ເຊິ່ງເອີ້ນກັນວ່າ loculus Archimedius ແລະຍັງເປັນ syntomachion , ແມ່ນສົນທິສັນຍາທາງຄະນິດສາດທີ່ມີຊື່ວ່າ Archimedes. ຜົນງານດັ່ງກ່າວໄດ້ລອດຊີວິດມາເປັນສ່ວນ ໜຶ່ງ ໃນສະບັບພາສາອາຣັບແລະ ສຳ ເນົາ, ໜັງ ສື Archimedes Palimpsest , ຂອງຕົວ ໜັງ ສືກເຣັກເກົ່າແກ່ທີ່ຜະລິດໃນຍຸກ Byzantine ຄຳ ວ່າ Ostomachion ມີຕົ້ນ ກຳ ເນີດມາຈາກພາສາກະເຣັກὈστομάχιονເຊິ່ງມີຄວາມ ໝາຍ ວ່າ "ການຕໍ່ສູ້ກັບກະດູກ", ຈາກὀστέον ( osteon ), "ກະດູກ" ແລະμάχη ( mache ), "ການຕໍ່ສູ້, ການຕໍ່ສູ້, ການຕໍ່ສູ້". ໃຫ້ສັງເກດວ່າ ໜັງ ສືໃບລານອ້າງເຖິງ ຄຳ ວ່າ " Stomachion " ເຊິ່ງເປັນການສໍ້ລາດບັງຫຼວງທີ່ປາກົດຂື້ນມາຈາກພາສາກະເຣັກເດີມ. Ausonius ໃຫ້ພວກເຮົາມີຊື່ທີ່ຖືກຕ້ອງວ່າ "Ostomachion". The Ostomachion ທີ່ລາວອະທິບາຍແມ່ນປິດສະ ໜາ ຄ້າຍຄືກັບຮູບຊົງກະຈົກແລະຖືກຫຼີ້ນບາງທີໂດຍຫຼາຍໆຄົນທີ່ມີກະດູກເຮັດ. ມັນບໍ່ເປັນທີ່ຮູ້ຈັກວ່າມີອາຍຸໃດ, ການສືບສວນທາງເລຂາຄະນິດຂອງ Archimedes ກ່ຽວກັບຕົວເລກ, ຫລືເກມ. Victorinus, Bassus Ennodius ແລະ Lucretius ໄດ້ເວົ້າກ່ຽວກັບເກມເຊັ່ນກັນ.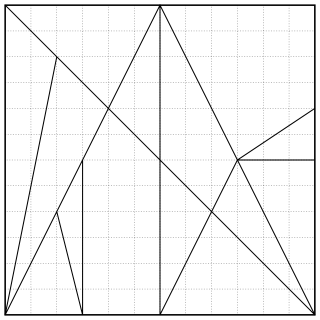
axioms ຂອງ Hilbert: axioms ຂອງ Hilbert ແມ່ນຊຸດຂອງ 20 ສົມມຸດຕິຖານທີ່ສະເຫນີໂດຍ David Hilbert ໃນປີ 1899 ໃນປື້ມ Grundlagen der Geometrie ຂອງລາວ ເປັນພື້ນຖານສໍາລັບການປິ່ນປົວທີ່ທັນສະໄຫມຂອງເລຂາຄະນິດ Euclidean. axiomatization ທັນສະໄຫມທີ່ມີຊື່ສຽງຂອງເລຂາຄະນິດຂອງ Euclidean ແມ່ນຂອງ Alfred Tarski ແລະຂອງ George Birkhoff.
Eureka (ຄຳ ສັບ): Eureka ແມ່ນ ຄຳ ສັບທີ່ໃຊ້ເພື່ອສະເຫຼີມສະຫຼອງການຄົ້ນພົບຫຼືການປະດິດສ້າງ. ມັນແມ່ນການແປ ຄຳ ອຸທອນທີ່ເວົ້າເຖິງນັກຄະນິດສາດຊາວເກຣັກບູຮານແລະນັກປະດິດ Archimedes.
ບັນຫາການລ້ຽງສັດຂອງ Archimedes: ບັນຫາການລ້ຽງສັດຂອງ Archimedes ແມ່ນເປັນປັນຫາໃນການວິເຄາະ Diophantine, ການສຶກສາສົມຜົນຂອງ polynomial ກັບວິທີແກ້ໄຂແບບເຕັມ. ເນື່ອງຈາກ Archimedes, ບັນຫາກ່ຽວຂ້ອງກັບການຄິດໄລ່ ຈຳ ນວນງົວໃນຝູງສັດພະເຈົ້າແສງຕາເວັນຈາກຂໍ້ ຈຳ ກັດທີ່ ກຳ ນົດໄວ້. ບັນຫາດັ່ງກ່າວຖືກຄົ້ນພົບໂດຍ Gotthold Ephraim Lessing ໃນ ໜັງ ສືໃບລານກເຣັກບັນຈຸບົດກະວີຂອງສີ່ສິບສີ່ເສັ້ນ, ໃນຫໍສະ ໝຸດ Herzog August ໃນWolfenbüttel, ປະເທດເຢຍລະມັນໃນປີ 1773.
ວົງຄູ່ແຝດ: ໃນຮູບເລຂາຄະນິດ, ວົງຄູ່ແຝດ ແມ່ນສອງວົງພິເສດທີ່ກ່ຽວຂ້ອງກັບ arbelos.An arbelos ຖືກ ກຳ ນົດໂດຍສາມຈຸດ collinear A , B , ແລະ C , ແລະເປັນເຂດສາມຫລ່ຽມໂຄ້ງມົນລະຫວ່າງສາມຫລ່ຽມວົງຈອນທີ່ມີ AB , BC , ແລະ AC ເປັນຂອງພວກເຂົາ ເສັ້ນຜ່າສູນກາງ. ຖ້າ arbelos ຖືກແບ່ງອອກເປັນສອງຂົງເຂດນ້ອຍໆໂດຍແບ່ງສາຍໂດຍຜ່ານຈຸດສູນກາງຂອງ A , B , ແລະ C , ຕາມເສັ້ນສາຍ ABC , ຫຼັງຈາກນັ້ນ, ວົງແຫວນຄູ່ແຝດທັງສອງຢູ່ໃນ ໜຶ່ງ ໃນສອງພາກພື້ນນີ້, ກົງກັນຂ້າມກັບສອງ semicircular ຂອງມັນ ທັງສອງດ້ານແລະສ່ວນທີ່ແຕກແຍກ.
ວົງຄູ່ແຝດ: ໃນຮູບເລຂາຄະນິດ, ວົງຄູ່ແຝດ ແມ່ນສອງວົງພິເສດທີ່ກ່ຽວຂ້ອງກັບ arbelos.An arbelos ຖືກ ກຳ ນົດໂດຍສາມຈຸດ collinear A , B , ແລະ C , ແລະເປັນເຂດສາມຫລ່ຽມໂຄ້ງມົນລະຫວ່າງສາມຫລ່ຽມວົງຈອນທີ່ມີ AB , BC , ແລະ AC ເປັນຂອງພວກເຂົາ ເສັ້ນຜ່າສູນກາງ. ຖ້າ arbelos ຖືກແບ່ງອອກເປັນສອງຂົງເຂດນ້ອຍໆໂດຍແບ່ງສາຍໂດຍຜ່ານຈຸດສູນກາງຂອງ A , B , ແລະ C , ຕາມເສັ້ນສາຍ ABC , ຫຼັງຈາກນັ້ນ, ວົງແຫວນຄູ່ແຝດທັງສອງຢູ່ໃນ ໜຶ່ງ ໃນສອງພາກພື້ນນີ້, ກົງກັນຂ້າມກັບສອງ semicircular ຂອງມັນ ທັງສອງດ້ານແລະສ່ວນທີ່ແຕກແຍກ.
Pi: ໝາຍ ເລກ π ແມ່ນເລກຄະນິດສາດຄົງທີ່. ມັນຖືກ ກຳ ນົດເປັນອັດຕາສ່ວນຂອງວົງກົມຂອງວົງກົມກັບເສັ້ນຜ່າສູນກາງຂອງມັນ, ແລະມັນຍັງມີ ຄຳ ນິຍາມທຽບເທົ່າກັນ. ມັນປະກົດຢູ່ໃນຫຼາຍສູດໃນທຸກຂົງເຂດຂອງຄະນິດສາດແລະຟີຊິກ. ການນໍາໃຊ້ເປັນທີ່ຮູ້ຈັກທໍາອິດຂອງπຈົດຫມາຍສະບັບກເຣັກເປັນຕົວແທນຂອງອັດຕາສ່ວນຂອງ circumference ວົງຂອງເສັ້ນຜ່າສູນກາງຂອງຕົນແມ່ນ by ແວວນັກຄະນິດສາດ William Jones ໃນ 1706. ມັນແມ່ນປະມານເທົ່າທຽມກັນທີ່ 3,14159. ມັນໄດ້ຖືກສະແດງໂດຍຕົວອັກສອນກະເຣັກ " π " ຕັ້ງແຕ່ກາງສະຕະວັດທີ 18, ແລະຖືກສະກົດອອກເປັນ " pi ". ມັນຍັງຖືກເອີ້ນວ່າຄົງທີ່ຂອງ Archimedes .
axioms ຂອງ Hilbert: axioms ຂອງ Hilbert ແມ່ນຊຸດຂອງ 20 ສົມມຸດຕິຖານທີ່ສະເຫນີໂດຍ David Hilbert ໃນປີ 1899 ໃນປື້ມ Grundlagen der Geometrie ຂອງລາວ ເປັນພື້ນຖານສໍາລັບການປິ່ນປົວທີ່ທັນສະໄຫມຂອງເລຂາຄະນິດ Euclidean. axiomatization ທັນສະໄຫມທີ່ມີຊື່ສຽງຂອງເລຂາຄະນິດຂອງ Euclidean ແມ່ນຂອງ Alfred Tarski ແລະຂອງ George Birkhoff.
ໝາຍ ເລກ Archimedes: ໃນນະໂຍບາຍດ້ານນ້ ຳ viscous, ຈຳ ນວນ Archimedes ( Ar ), ແມ່ນ ຈຳ ນວນມິຕິທີ່ໃຊ້ໃນການ ກຳ ນົດການເຄື່ອນໄຫວຂອງທາດແຫຼວຍ້ອນຄວາມແຕກຕ່າງຄວາມ ໜາ ແໜ້ນ, ຕັ້ງຊື່ຕາມນັກວິທະຍາສາດແລະນັກຄະນິດສາດຊາວເກຼັກບູຮານ Archimedes.
Ostomachion: Ostomachion , ເຊິ່ງເອີ້ນກັນວ່າ loculus Archimedius ແລະຍັງເປັນ syntomachion , ແມ່ນສົນທິສັນຍາທາງຄະນິດສາດທີ່ມີຊື່ວ່າ Archimedes. ຜົນງານດັ່ງກ່າວໄດ້ລອດຊີວິດມາເປັນສ່ວນ ໜຶ່ງ ໃນສະບັບພາສາອາຣັບແລະ ສຳ ເນົາ, ໜັງ ສື Archimedes Palimpsest , ຂອງຕົວ ໜັງ ສືກເຣັກເກົ່າແກ່ທີ່ຜະລິດໃນຍຸກ Byzantine ຄຳ ວ່າ Ostomachion ມີຕົ້ນ ກຳ ເນີດມາຈາກພາສາກະເຣັກὈστομάχιονເຊິ່ງມີຄວາມ ໝາຍ ວ່າ "ການຕໍ່ສູ້ກັບກະດູກ", ຈາກὀστέον ( osteon ), "ກະດູກ" ແລະμάχη ( mache ), "ການຕໍ່ສູ້, ການຕໍ່ສູ້, ການຕໍ່ສູ້". ໃຫ້ສັງເກດວ່າ ໜັງ ສືໃບລານອ້າງເຖິງ ຄຳ ວ່າ " Stomachion " ເຊິ່ງເປັນການສໍ້ລາດບັງຫຼວງທີ່ປາກົດຂື້ນມາຈາກພາສາກະເຣັກເດີມ. Ausonius ໃຫ້ພວກເຮົາມີຊື່ທີ່ຖືກຕ້ອງວ່າ "Ostomachion". The Ostomachion ທີ່ລາວອະທິບາຍແມ່ນປິດສະ ໜາ ຄ້າຍຄືກັບຮູບຊົງກະຈົກແລະຖືກຫຼີ້ນບາງທີໂດຍຫຼາຍໆຄົນທີ່ມີກະດູກເຮັດ. ມັນບໍ່ເປັນທີ່ຮູ້ຈັກວ່າມີອາຍຸໃດ, ການສືບສວນທາງເລຂາຄະນິດຂອງ Archimedes ກ່ຽວກັບຕົວເລກ, ຫລືເກມ. Victorinus, Bassus Ennodius ແລະ Lucretius ໄດ້ເວົ້າກ່ຽວກັບເກມເຊັ່ນກັນ.
ການປ່ຽນແປງຂອງແຮງດັນແບບແນວຕັ້ງ: ການປ່ຽນແປງຂອງຄວາມກົດດັນແບບແນວຕັ້ງ ແມ່ນການປ່ຽນແປງຂອງຄວາມກົດດັນທີ່ເປັນ ໜ້າ ທີ່ຂອງການສູງ. ອີງຕາມທາດແຫຼວໃນ ຄຳ ຖາມແລະສະພາບການທີ່ຖືກກ່າວເຖິງ, ມັນອາດຈະມີຄວາມແຕກຕ່າງກັນຢ່າງຫຼວງຫຼາຍໃນແຕ່ລະດ້ານຕາມລວງກວ້າງເຊັ່ນດຽວກັນ, ແລະການປ່ຽນແປງເຫຼົ່ານີ້ມີຄວາມກ່ຽວຂ້ອງໃນສະພາບການຂອງແຮງກົດດັນແລະຜົນກະທົບຂອງມັນ. ເຖິງຢ່າງໃດກໍ່ຕາມ, ການປ່ຽນແປງທາງແນວຕັ້ງແມ່ນມີຄວາມ ສຳ ຄັນເປັນພິເສດ, ຍ້ອນວ່າມັນເປັນຜົນມາຈາກການດຶງແຮງໂນ້ມຖ່ວງໃສ່ທາດແຫຼວ; ຄືກັນກັບ ສຳ ລັບນ້ ຳ ທີ່ໃຫ້ໃນລະດັບດຽວກັນ, ການຫຼຸດລົງຂອງລະດັບຄວາມສູງພາຍໃນມັນເທົ່າກັບຖັນທີ່ສູງກວ່າຂອງນ້ ຳ ໜັກ ທີ່ມີນ້ ຳ ໜັກ ລົງໃນຈຸດນັ້ນ.
axioms ຂອງ Hilbert: axioms ຂອງ Hilbert ແມ່ນຊຸດຂອງ 20 ສົມມຸດຕິຖານທີ່ສະເຫນີໂດຍ David Hilbert ໃນປີ 1899 ໃນປື້ມ Grundlagen der Geometrie ຂອງລາວ ເປັນພື້ນຖານສໍາລັບການປິ່ນປົວທີ່ທັນສະໄຫມຂອງເລຂາຄະນິດ Euclidean. axiomatization ທັນສະໄຫມທີ່ມີຊື່ສຽງຂອງເລຂາຄະນິດຂອງ Euclidean ແມ່ນຂອງ Alfred Tarski ແລະຂອງ George Birkhoff.
ຫຼັກການຂອງ Archimedes: ຫລັກການຂອງ Archimedes ລະ ບຸວ່າແຮງກະຕຸ້ນທີ່ຂຶ້ນໄປເທິງທີ່ຖືກປ່ອຍອອກຈາກຮ່າງກາຍທີ່ຖືກຈຸ່ມລົງໃນນໍ້າ, ບໍ່ວ່າຈະເຕັມຫຼືບາງສ່ວນ, ເທົ່າກັບນ້ ຳ ໜັກ ຂອງທາດແຫຼວທີ່ຮ່າງກາຍຍ້າຍອອກ. ຫຼັກການຂອງ Archimedes ແມ່ນກົດ ໝາຍ ຂອງຟີຊິກພື້ນຖານຕໍ່ກັບກົນຈັກນ້ ຳ. ມັນຖືກສ້າງຂື້ນໂດຍ Archimedes of Syracuse.
ຮູບສີ່ຫລ່ຽມຂອງ Archimedes: ໃນຮູບເລຂາຄະນິດ, Archimedes 'quadruplets' ແມ່ນສີ່ວົງກົມໃຫຍ່ທີ່ກ່ຽວຂ້ອງກັບ arbelos. ແນະ ນຳ ໂດຍ Frank Power ໃນຊ່ວງລະດູຮ້ອນປີ 1998, ແຕ່ລະແຫ່ງມີເນື້ອທີ່ຄືກັນກັບວົງແຫວນຄູ່ແຝດ Archimedes, ເຮັດໃຫ້ພວກມັນເປັນວົງກົມ Archimedean.
ບັນຫາການລ້ຽງສັດຂອງ Archimedes: ບັນຫາການລ້ຽງສັດຂອງ Archimedes ແມ່ນເປັນປັນຫາໃນການວິເຄາະ Diophantine, ການສຶກສາສົມຜົນຂອງ polynomial ກັບວິທີແກ້ໄຂແບບເຕັມ. ເນື່ອງຈາກ Archimedes, ບັນຫາກ່ຽວຂ້ອງກັບການຄິດໄລ່ ຈຳ ນວນງົວໃນຝູງສັດພະເຈົ້າແສງຕາເວັນຈາກຂໍ້ ຈຳ ກັດທີ່ ກຳ ນົດໄວ້. ບັນຫາດັ່ງກ່າວຖືກຄົ້ນພົບໂດຍ Gotthold Ephraim Lessing ໃນ ໜັງ ສືໃບລານກເຣັກບັນຈຸບົດກະວີຂອງສີ່ສິບສີ່ເສັ້ນ, ໃນຫໍສະ ໝຸດ Herzog August ໃນWolfenbüttel, ປະເທດເຢຍລະມັນໃນປີ 1773.
ສະກູ Archimedes: ສະ ກູຂອງ Archimedes , ເຊິ່ງເອີ້ນກັນວ່າສະ ກູລະບາຍນ້ ຳ , ຈັກສູບ ນ້ ຳ ສະກູ ຫລືສະ ກູຂອງອີຢິບ , ແມ່ນເຄື່ອງຈັກທີ່ໃຊ້ ສຳ ລັບໂອນນ້ ຳ ຈາກຮ່າງກາຍຂອງນ້ ຳ ທີ່ຕ່ ຳ ລົງສູ່ຄອງຊົນລະປະທານ. ນໍ້າໄດ້ຖືກຈັກສູບໂດຍການຫັນ ໜ້າ ດິນທີ່ມີຮູບຮ່າງ screw ພາຍໃນທໍ່. ມັນຖືກຕັ້ງຊື່ຕາມນັກປັດຊະຍາຊາວເກຣັກ Archimedes ຜູ້ທີ່ໄດ້ບັນຍາຍມັນຄັ້ງ ທຳ ອິດປະມານ 234 ປີກ່ອນຄ. ສ. ເຄື່ອງເຈາະສະກູແມ່ນອຸປະກອນທີ່ຄ້າຍຄືກັນທີ່ສົ່ງວັດສະດຸສ່ວນໃຫຍ່ເຊັ່ນແປ້ງແລະເມັດພືດ.
ກັງຫັນເຈາະ: ກັງຫັນກັງ ຫລື Archimedean ແມ່ນ ກັງຫັນ ນ້ ຳ ເຊິ່ງໃຊ້ຫຼັກການຂອງ ໝໍ້ Archimedean ເພື່ອປ່ຽນພະລັງງານທີ່ມີທ່າແຮງຂອງນ້ ຳ ໃນລະດັບສູງຂື້ນສູ່ບ່ອນເຮັດວຽກ. ມັນອາດຈະຖືກປຽບທຽບກັບລໍ້ນໍ້າ. ກັງຫັນປະກອບມີໂລໂກ້ໃນຮູບຊົງຂອງສະກູ Archimedean ເຊິ່ງ ໝູນ ວຽນຢູ່ໃນເຕົ່າ semicircular. ນ້ ຳ ໄຫລເຂົ້າສູ່ກັງຫັນແລະນ້ ຳ ໜັກ ຂອງມັນກົດດັນລົງໃສ່ກ້ອງກັງຫັນ, ເຊິ່ງມັນຈະເຮັດໃຫ້ກັງຫັນປ່ຽນ. ນ້ ຳ ໄຫລອອກມາຢ່າງສິ້ນເຊີງຈາກສິ້ນກັງຫັນລົງສູ່ແມ່ນ້ ຳ. ສົ້ນດ້ານເທິງຂອງສະກູແມ່ນເຊື່ອມຕໍ່ກັບເຄື່ອງປັ່ນໄຟໂດຍຜ່ານກ່ອງເກຍ.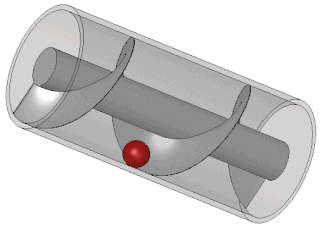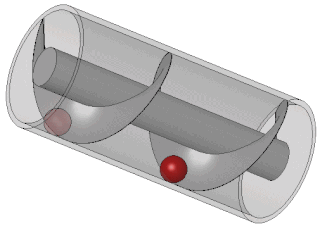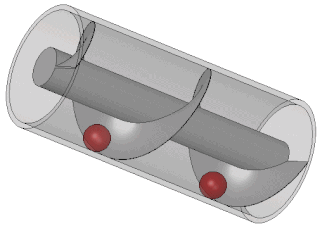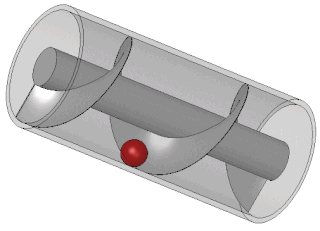
ກ້ຽວວຽນ Archimedean: ກ້ຽວວຽນ Archimedean ແມ່ນກ້ຽວວຽນທີ່ມີຊື່ຕາມສະກຸນ Archimedes ນັກຄະນິດສາດເຣັກໃນສະຕະວັດທີ 3 ກ່ອນຄ. ສ. ມັນແມ່ນສະຖານທີ່ທີ່ສອດຄ້ອງກັບສະຖານທີ່ຕ່າງໆຕາມການເວລາຂອງຈຸດທີ່ຍ້າຍອອກໄປຈາກຈຸດຄົງທີ່ທີ່ມີຄວາມໄວຄົງທີ່ຕາມເສັ້ນທີ່ ໝຸນ ກັບຄວາມໄວຂອງມຸມ. ເທົ່າທຽມກັນ, ໃນການປະສານງານຂົ້ວໂລກ ( r , θ ) ມັນສາມາດອະທິບາຍໄດ້ໂດຍສົມຜົນ
ຊັບສິນ Archimedean: ໃນຄະນິດສາດແລະການວິເຄາະທີ່ບໍ່ມີຕົວຕົນ, ຊັບສິນ Archimedean , ທີ່ຕັ້ງຊື່ຕາມຊື່ຄະນິດສາດຊັ້ນສູງຂອງເກຼັກ Archimedes of Syracuse, ແມ່ນຊັບສິນທີ່ຖືກຈັດຂື້ນໂດຍໂຄງສ້າງກ່ຽວກັບພຶດຊະຄະນິດບາງຢ່າງ, ເຊັ່ນ: ກຸ່ມທີ່ມີ ຄຳ ສັ່ງຫຼືມາດຕະຖານ, ແລະທົ່ງນາ. ຄຸນສົມບັດ, ທີ່ຖືກສ້າງຂື້ນໂດຍປົກກະຕິລະບຸວ່າໃຫ້ສອງຕົວເລກ x ແລະ y , ມັນຈະມີເລກເຕັມ n ເພື່ອວ່າ nx > y . ມັນຍັງຫມາຍຄວາມວ່າຊຸດຂອງຕົວເລກທໍາມະຊາດບໍ່ໄດ້ຖືກຜູກຢູ່ຂ້າງເທິງ. ເວົ້າໂດຍຫຍໍ້, ມັນແມ່ນຊັບສົມບັດຂອງການບໍ່ມີອົງປະກອບ ນ້ອຍ ຫລື ໃຫຍ່ທີ່ ບໍ່ມີຂອບເຂດ . ມັນແມ່ນ Otto Stolz ຜູ້ທີ່ໃຫ້ຊື່ຂອງ Archimedes ຍ້ອນວ່າມັນປະກົດວ່າເປັນ Axiom V ຂອງ Archimedes ' On the Sphere ແລະກະບອກ .
ຫຼັກການຂອງ Archimedes: ຫລັກການຂອງ Archimedes ລະ ບຸວ່າແຮງກະຕຸ້ນທີ່ຂຶ້ນໄປເທິງທີ່ຖືກປ່ອຍອອກຈາກຮ່າງກາຍທີ່ຖືກຈຸ່ມລົງໃນນໍ້າ, ບໍ່ວ່າຈະເຕັມຫຼືບາງສ່ວນ, ເທົ່າກັບນ້ ຳ ໜັກ ຂອງທາດແຫຼວທີ່ຮ່າງກາຍຍ້າຍອອກ. ຫຼັກການຂອງ Archimedes ແມ່ນກົດ ໝາຍ ຂອງຟີຊິກພື້ນຖານຕໍ່ກັບກົນຈັກນ້ ຳ. ມັນຖືກສ້າງຂື້ນໂດຍ Archimedes of Syracuse.
ວົງຄູ່ແຝດ: ໃນຮູບເລຂາຄະນິດ, ວົງຄູ່ແຝດ ແມ່ນສອງວົງພິເສດທີ່ກ່ຽວຂ້ອງກັບ arbelos.An arbelos ຖືກ ກຳ ນົດໂດຍສາມຈຸດ collinear A , B , ແລະ C , ແລະເປັນເຂດສາມຫລ່ຽມໂຄ້ງມົນລະຫວ່າງສາມຫລ່ຽມວົງຈອນທີ່ມີ AB , BC , ແລະ AC ເປັນຂອງພວກເຂົາ ເສັ້ນຜ່າສູນກາງ. ຖ້າ arbelos ຖືກແບ່ງອອກເປັນສອງຂົງເຂດນ້ອຍໆໂດຍແບ່ງສາຍໂດຍຜ່ານຈຸດສູນກາງຂອງ A , B , ແລະ C , ຕາມເສັ້ນສາຍ ABC , ຫຼັງຈາກນັ້ນ, ວົງແຫວນຄູ່ແຝດທັງສອງຢູ່ໃນ ໜຶ່ງ ໃນສອງພາກພື້ນນີ້, ກົງກັນຂ້າມກັບສອງ semicircular ຂອງມັນ ທັງສອງດ້ານແລະສ່ວນທີ່ແຕກແຍກ.
ວິທີການຂອງທິດສະດີກົນຈັກ: ວິທີການກ່ຽວກັບທິດສະດີກົນຈັກ , ຍັງຖືກເອີ້ນວ່າ The Method , ຖືວ່າເປັນ ໜຶ່ງ ໃນບັນດາຜົນງານທີ່ມີຊີວິດລອດທີ່ ສຳ ຄັນຂອງ Polymath Archimedes ຂອງກເຣັກໂບຮານ. ວິທີໃຊ້ເວລາຮູບແບບຂອງຈົດຫມາຍສະບັບຈາກ Archimedes ກັບ Eratosthenes, ຫ້ອງສະຫມຸດຫົວຫນ້າຢູ່ຫໍສະຫມຸດຂອງ Alexandria ໄດ້, ແລະປະກອບດ້ວຍທໍາອິດ attested ໃຊ້ຢ່າງຊັດເຈນຂອງຕັດແຍກອອກ. ວຽກງານດັ່ງກ່າວໄດ້ຖືກຄິດໃນເບື້ອງຕົ້ນວ່າຈະຫາຍໄປ, ແຕ່ໃນປີ 1906 ໄດ້ຖືກຄົ້ນພົບຄືນ ໃໝ່ ໃນງານສະເຫຼີມສະຫຼອງ Archimedes Palimpsest. palimpsest ປະກອບມີບັນຊີຂອງ Archimedes ກ່ຽວກັບ "ວິທີການກົນຈັກ", ດັ່ງນັ້ນເອີ້ນວ່າຍ້ອນວ່າມັນອີງໃສ່ກົດຫມາຍຂອງ lever, ເຊິ່ງໄດ້ຖືກສະແດງໃຫ້ເຫັນຄັ້ງທໍາອິດໂດຍ Archimedes, ແລະສູນກາງຂອງມະຫາຊົນ, ເຊິ່ງລາວໄດ້ພົບເຫັນຫລາຍຮູບແບບພິເສດ.
Buoyancy: Buoyancy , ຫຼື upthrust , ແມ່ນຜົນບັງຄັບໃຊ້ທີ່ຂື້ນຂື້ນຂ້າງເທິງໂດຍທາດແຫຼວທີ່ຕໍ່ຕ້ານກັບນ້ ຳ ໜັກ ຂອງວັດຖຸບາງສ່ວນຫຼືບາງສ່ວນທີ່ຝັງເລິກ. ໃນຖັນຂອງນ້ ຳ, ຄວາມກົດດັນເພີ່ມຂື້ນດ້ວຍຄວາມເລິກເຊິ່ງເປັນຜົນມາຈາກນ້ ຳ ໜັກ ຂອງນ້ ຳ ທີ່ລົ້ນ. ດັ່ງນັ້ນຄວາມກົດດັນທີ່ຢູ່ທາງລຸ່ມຂອງຖັນຂອງແຫຼວແມ່ນໃຫຍ່ກວ່າຢູ່ດ້ານເທິງຂອງຖັນ. ເຊັ່ນດຽວກັນ, ຄວາມກົດດັນຢູ່ທາງລຸ່ມຂອງວັດຖຸທີ່ຖືກຈຸ່ມລົງໃນນໍ້າຈະໃຫຍ່ກວ່າຢູ່ເທິງສຸດຂອງວັດຖຸ. ຄວາມແຕກຕ່າງຂອງຄວາມກົດດັນສົ່ງຜົນໃຫ້ມີການຂື້ນເທິງສຸດຂອງວັດຖຸ. ຂະ ໜາດ ຂອງຜົນບັງຄັບໃຊ້ແມ່ນອັດຕາສ່ວນກັບຄວາມແຕກຕ່າງຂອງຄວາມກົດດັນ, ແລະທຽບເທົ່າກັບນ້ ຳ ໜັກ ຂອງແຫຼວທີ່ຖ້າບໍ່ດັ່ງນັ້ນຈະຍຶດເອົາປະລິມານທີ່ຂົມລົງຂອງວັດຖຸເຊັ່ນ: ນ້ ຳ ທີ່ຖືກຍົກຍ້າຍ.
axioms ຂອງ Hilbert: axioms ຂອງ Hilbert ແມ່ນຊຸດຂອງ 20 ສົມມຸດຕິຖານທີ່ສະເຫນີໂດຍ David Hilbert ໃນປີ 1899 ໃນປື້ມ Grundlagen der Geometrie ຂອງລາວ ເປັນພື້ນຖານສໍາລັບການປິ່ນປົວທີ່ທັນສະໄຫມຂອງເລຂາຄະນິດ Euclidean. axiomatization ທັນສະໄຫມທີ່ມີຊື່ສຽງຂອງເລຂາຄະນິດຂອງ Euclidean ແມ່ນຂອງ Alfred Tarski ແລະຂອງ George Birkhoff.
ບັນຫາການລ້ຽງສັດຂອງ Archimedes: ບັນຫາການລ້ຽງສັດຂອງ Archimedes ແມ່ນເປັນປັນຫາໃນການວິເຄາະ Diophantine, ການສຶກສາສົມຜົນຂອງ polynomial ກັບວິທີແກ້ໄຂແບບເຕັມ. ເນື່ອງຈາກ Archimedes, ບັນຫາກ່ຽວຂ້ອງກັບການຄິດໄລ່ ຈຳ ນວນງົວໃນຝູງສັດພະເຈົ້າແສງຕາເວັນຈາກຂໍ້ ຈຳ ກັດທີ່ ກຳ ນົດໄວ້. ບັນຫາດັ່ງກ່າວຖືກຄົ້ນພົບໂດຍ Gotthold Ephraim Lessing ໃນ ໜັງ ສືໃບລານກເຣັກບັນຈຸບົດກະວີຂອງສີ່ສິບສີ່ເສັ້ນ, ໃນຫໍສະ ໝຸດ Herzog August ໃນWolfenbüttel, ປະເທດເຢຍລະມັນໃນປີ 1773.
Pi: ໝາຍ ເລກ π ແມ່ນເລກຄະນິດສາດຄົງທີ່. ມັນຖືກ ກຳ ນົດເປັນອັດຕາສ່ວນຂອງວົງກົມຂອງວົງກົມກັບເສັ້ນຜ່າສູນກາງຂອງມັນ, ແລະມັນຍັງມີ ຄຳ ນິຍາມທຽບເທົ່າກັນ. ມັນປະກົດຢູ່ໃນຫຼາຍສູດໃນທຸກຂົງເຂດຂອງຄະນິດສາດແລະຟີຊິກ. ການນໍາໃຊ້ເປັນທີ່ຮູ້ຈັກທໍາອິດຂອງπຈົດຫມາຍສະບັບກເຣັກເປັນຕົວແທນຂອງອັດຕາສ່ວນຂອງ circumference ວົງຂອງເສັ້ນຜ່າສູນກາງຂອງຕົນແມ່ນ by ແວວນັກຄະນິດສາດ William Jones ໃນ 1706. ມັນແມ່ນປະມານເທົ່າທຽມກັນທີ່ 3,14159. ມັນໄດ້ຖືກສະແດງໂດຍຕົວອັກສອນກະເຣັກ " π " ຕັ້ງແຕ່ກາງສະຕະວັດທີ 18, ແລະຖືກສະກົດອອກເປັນ " pi ". ມັນຍັງຖືກເອີ້ນວ່າຄົງທີ່ຂອງ Archimedes .
ຫຼັກການຂອງ Archimedes: ຫລັກການຂອງ Archimedes ລະ ບຸວ່າແຮງກະຕຸ້ນທີ່ຂຶ້ນໄປເທິງທີ່ຖືກປ່ອຍອອກຈາກຮ່າງກາຍທີ່ຖືກຈຸ່ມລົງໃນນໍ້າ, ບໍ່ວ່າຈະເຕັມຫຼືບາງສ່ວນ, ເທົ່າກັບນ້ ຳ ໜັກ ຂອງທາດແຫຼວທີ່ຮ່າງກາຍຍ້າຍອອກ. ຫຼັກການຂອງ Archimedes ແມ່ນກົດ ໝາຍ ຂອງຟີຊິກພື້ນຖານຕໍ່ກັບກົນຈັກນ້ ຳ. ມັນຖືກສ້າງຂື້ນໂດຍ Archimedes of Syracuse.
ສະກູ Archimedes: ສະ ກູຂອງ Archimedes , ເຊິ່ງເອີ້ນກັນວ່າສະ ກູລະບາຍນ້ ຳ , ຈັກສູບ ນ້ ຳ ສະກູ ຫລືສະ ກູຂອງອີຢິບ , ແມ່ນເຄື່ອງຈັກທີ່ໃຊ້ ສຳ ລັບໂອນນ້ ຳ ຈາກຮ່າງກາຍຂອງນ້ ຳ ທີ່ຕ່ ຳ ລົງສູ່ຄອງຊົນລະປະທານ. ນໍ້າໄດ້ຖືກຈັກສູບໂດຍການຫັນ ໜ້າ ດິນທີ່ມີຮູບຮ່າງ screw ພາຍໃນທໍ່. ມັນຖືກຕັ້ງຊື່ຕາມນັກປັດຊະຍາຊາວເກຣັກ Archimedes ຜູ້ທີ່ໄດ້ບັນຍາຍມັນຄັ້ງ ທຳ ອິດປະມານ 234 ປີກ່ອນຄ. ສ. ເຄື່ອງເຈາະສະກູແມ່ນອຸປະກອນທີ່ຄ້າຍຄືກັນທີ່ສົ່ງວັດສະດຸສ່ວນໃຫຍ່ເຊັ່ນແປ້ງແລະເມັດພືດ.
ກ້ຽວວຽນ Archimedean: ກ້ຽວວຽນ Archimedean ແມ່ນກ້ຽວວຽນທີ່ມີຊື່ຕາມສະກຸນ Archimedes ນັກຄະນິດສາດເຣັກໃນສະຕະວັດທີ 3 ກ່ອນຄ. ສ. ມັນແມ່ນສະຖານທີ່ທີ່ສອດຄ້ອງກັບສະຖານທີ່ຕ່າງໆຕາມການເວລາຂອງຈຸດທີ່ຍ້າຍອອກໄປຈາກຈຸດຄົງທີ່ທີ່ມີຄວາມໄວຄົງທີ່ຕາມເສັ້ນທີ່ ໝຸນ ກັບຄວາມໄວຂອງມຸມ. ເທົ່າທຽມກັນ, ໃນການປະສານງານຂົ້ວໂລກ ( r , θ ) ມັນສາມາດອະທິບາຍໄດ້ໂດຍສົມຜົນ
ວົງຄູ່ແຝດ: ໃນຮູບເລຂາຄະນິດ, ວົງຄູ່ແຝດ ແມ່ນສອງວົງພິເສດທີ່ກ່ຽວຂ້ອງກັບ arbelos.An arbelos ຖືກ ກຳ ນົດໂດຍສາມຈຸດ collinear A , B , ແລະ C , ແລະເປັນເຂດສາມຫລ່ຽມໂຄ້ງມົນລະຫວ່າງສາມຫລ່ຽມວົງຈອນທີ່ມີ AB , BC , ແລະ AC ເປັນຂອງພວກເຂົາ ເສັ້ນຜ່າສູນກາງ. ຖ້າ arbelos ຖືກແບ່ງອອກເປັນສອງຂົງເຂດນ້ອຍໆໂດຍແບ່ງສາຍໂດຍຜ່ານຈຸດສູນກາງຂອງ A , B , ແລະ C , ຕາມເສັ້ນສາຍ ABC , ຫຼັງຈາກນັ້ນ, ວົງແຫວນຄູ່ແຝດທັງສອງຢູ່ໃນ ໜຶ່ງ ໃນສອງພາກພື້ນນີ້, ກົງກັນຂ້າມກັບສອງ semicircular ຂອງມັນ ທັງສອງດ້ານແລະສ່ວນທີ່ແຕກແຍກ.
ວິທີການຂອງທິດສະດີກົນຈັກ: ວິທີການກ່ຽວກັບທິດສະດີກົນຈັກ , ຍັງຖືກເອີ້ນວ່າ The Method , ຖືວ່າເປັນ ໜຶ່ງ ໃນບັນດາຜົນງານທີ່ມີຊີວິດລອດທີ່ ສຳ ຄັນຂອງ Polymath Archimedes ຂອງກເຣັກໂບຮານ. ວິທີໃຊ້ເວລາຮູບແບບຂອງຈົດຫມາຍສະບັບຈາກ Archimedes ກັບ Eratosthenes, ຫ້ອງສະຫມຸດຫົວຫນ້າຢູ່ຫໍສະຫມຸດຂອງ Alexandria ໄດ້, ແລະປະກອບດ້ວຍທໍາອິດ attested ໃຊ້ຢ່າງຊັດເຈນຂອງຕັດແຍກອອກ. ວຽກງານດັ່ງກ່າວໄດ້ຖືກຄິດໃນເບື້ອງຕົ້ນວ່າຈະຫາຍໄປ, ແຕ່ໃນປີ 1906 ໄດ້ຖືກຄົ້ນພົບຄືນ ໃໝ່ ໃນງານສະເຫຼີມສະຫຼອງ Archimedes Palimpsest. palimpsest ປະກອບມີບັນຊີຂອງ Archimedes ກ່ຽວກັບ "ວິທີການກົນຈັກ", ດັ່ງນັ້ນເອີ້ນວ່າຍ້ອນວ່າມັນອີງໃສ່ກົດຫມາຍຂອງ lever, ເຊິ່ງໄດ້ຖືກສະແດງໃຫ້ເຫັນຄັ້ງທໍາອິດໂດຍ Archimedes, ແລະສູນກາງຂອງມະຫາຊົນ, ເຊິ່ງລາວໄດ້ພົບເຫັນຫລາຍຮູບແບບພິເສດ.
David M. Eddy: David M. Eddy ແມ່ນນັກວິຊາການແພດ, ນັກວິຊາການດ້ານຈິດຕະສາດ, ແລະນັກວິເຄາະດ້ານສຸຂະພາບອາເມລິກາເຊິ່ງໄດ້ເຮັດວຽກໃນການຮຽນແບບທາງດ້ານຄະນິດສາດຂອງບັນດາພະຍາດ, ຄຳ ແນະ ນຳ ໃນການປະຕິບັດດ້ານຄລີນິກ, ແລະຢາທີ່ອີງໃສ່ຫຼັກຖານ. 4 ຈຸດເດັ່ນຂອງການເຮັດວຽກຂອງລາວໄດ້ຖືກສະຫຼຸບໂດຍສະຖາບັນການແພດສະຖາບັນວິທະຍາສາດແຫ່ງຊາດວ່າ:" ຫຼາຍກວ່າ 25 ປີທີ່ຜ່ານມາ, Eddy ໄດ້ຂຽນບົດ ສຳ ມະນາກ່ຽວກັບບົດບາດຂອງ ຄຳ ແນະ ນຳ ໃນການຕັດສິນໃຈດ້ານການແພດ, ຮູບແບບ Markov ທຳ ອິດທີ່ ນຳ ໃຊ້ກັບຄລີນິກ ບັນຫາ, ແລະມາດຖານຕົ້ນສະບັບ ສຳ ລັບການຕັດສິນໃຈຄຸ້ມຄອງ; ລາວແມ່ນຜູ້ ທຳ ອິດທີ່ໃຊ້ແລະເຜີຍແຜ່ ຄຳ ວ່າ 'ອີງໃສ່ຫຼັກຖານ'.
David M. Eddy: David M. Eddy ແມ່ນນັກວິຊາການແພດ, ນັກວິຊາການດ້ານຈິດຕະສາດ, ແລະນັກວິເຄາະດ້ານສຸຂະພາບອາເມລິກາເຊິ່ງໄດ້ເຮັດວຽກໃນການຮຽນແບບທາງດ້ານຄະນິດສາດຂອງບັນດາພະຍາດ, ຄຳ ແນະ ນຳ ໃນການປະຕິບັດດ້ານຄລີນິກ, ແລະຢາທີ່ອີງໃສ່ຫຼັກຖານ. 4 ຈຸດເດັ່ນຂອງການເຮັດວຽກຂອງລາວໄດ້ຖືກສະຫຼຸບໂດຍສະຖາບັນການແພດສະຖາບັນວິທະຍາສາດແຫ່ງຊາດວ່າ:" ຫຼາຍກວ່າ 25 ປີທີ່ຜ່ານມາ, Eddy ໄດ້ຂຽນບົດ ສຳ ມະນາກ່ຽວກັບບົດບາດຂອງ ຄຳ ແນະ ນຳ ໃນການຕັດສິນໃຈດ້ານການແພດ, ຮູບແບບ Markov ທຳ ອິດທີ່ ນຳ ໃຊ້ກັບຄລີນິກ ບັນຫາ, ແລະມາດຖານຕົ້ນສະບັບ ສຳ ລັບການຕັດສິນໃຈຄຸ້ມຄອງ; ລາວແມ່ນຜູ້ ທຳ ອິດທີ່ໃຊ້ແລະເຜີຍແຜ່ ຄຳ ວ່າ 'ອີງໃສ່ຫຼັກຖານ'.
Archimedes-lab.org: Archimedes-lab.org ແມ່ນໂຄງການພັດທະນາໂດຍບໍ່ເສຍຄ່າແລະຮ່ວມມືກັນພັດທະນາແລະຮັກສາໂດຍ Gianni A. Sarcone ແລະ Marie-Jo Waeber, ນັກຂຽນແລະນັກຂຽນສອງຄົນທີ່ມີປະສົບການຫລາຍກ່ວາສາມສິບປີໃນຂົງເຂດແນວຄິດສາຍຕາແລະການສຶກສາ. ໂຄງການການສຶກສານີ້ແມ່ນສ່ວນ ໜຶ່ງ ຂອງອົງ ການ Open Education Consortium ແລະມັນຖືກຄວບຄຸມໂດຍເຄືອຂ່າຍທີ່ປຶກສາຂອງຜູ້ຊ່ຽວຊານທີ່ຊ່ຽວຊານດ້ານການສຶກສາທາງອິນເຕີເນັດ.
Archimedes (1797): Archimedes ໄດ້ຖືກເປີດຕົວຢູ່ທີ່ Sunderland ໃນປີ 1796 ຫຼື 1797. ນາງໄດ້ຊື້ຂາຍລະຫວ່າງອັງກິດແລະ Baltic ຈົນກ່ວາລັດຖະບານອັງກິດໄດ້ປະຕິບັດໃຫ້ນາງເປັນລົດຂົນສົ່ງ c.1809. ນາງໄດ້ສູນເສຍໄປໃນເດືອນທັນວາ 1811 ໃນຂະນະທີ່ກັບມາຈາກບານຕິກ.
Archimedes (bryozoan): Archimedes ແມ່ນສະກຸນຂອງ bryozoans ທີ່ເປັນຂອງຄອບຄົວ Fenestellidae. ການ ນຳ ໃຊ້ ຄຳ ສັບທີ່ມີຊື່ວ່າ Archimedes ຄັ້ງ ທຳ ອິດໃນປີ 1838.
Archimedes (CAD): Archimedes - "The Open CAD" - ແມ່ນໂປແກຼມອອກແບບທີ່ຊ່ວຍໃຫ້ຄອມພິວເຕີ້ (CAD) ກຳ ລັງຖືກພັດທະນາດ້ວຍການປ້ອນຂໍ້ມູນໂດຍກົງຈາກສະຖາປະນິກແລະບໍລິສັດສະຖາປັດຕະຍະ ກຳ. ດ້ວຍປັດຊະຍາການອອກແບບນີ້, ນັກພັດທະນາຫວັງວ່າຈະສ້າງໂປແກຼມທີ່ ເໝາະ ສົມກັບສະຖາປັດຕະຍະ ກຳ ກ່ວາ AutoCAD ທີ່ມີການ ນຳ ໃຊ້ຢ່າງກວ້າງຂວາງໃນປະຈຸບັນ, ແລະຊອບແວ CAD ອື່ນໆ. ໂປແກຼມແມ່ນຊອບແວເສລີທີ່ປ່ອຍອອກມາພາຍໃຕ້ໃບອະນຸຍາດສາທາລະນະ Eclipse.
Archimedes (bryozoan): Archimedes ແມ່ນສະກຸນຂອງ bryozoans ທີ່ເປັນຂອງຄອບຄົວ Fenestellidae. ການ ນຳ ໃຊ້ ຄຳ ສັບທີ່ມີຊື່ວ່າ Archimedes ຄັ້ງ ທຳ ອິດໃນປີ 1838.
Archimedes ຫມາກ: Acorn Archimedes ແມ່ນຄອບຄົວຄອມພິວເຕີສ່ວນບຸກຄົນທີ່ຖືກອອກແບບໂດຍ Acorn Computers ຂອງ Cambridge, ປະເທດອັງກິດ. ລະບົບດັ່ງກ່າວແມ່ນອີງໃສ່ໂປແກຼມສະຖາປັດຕະຍະ ກຳ ARM ຂອງ Acorn ເອງແລະລະບົບປະຕິບັດການທີ່ເປັນເຈົ້າຂອງ Arthur ແລະ RISC OS. ຮູບແບບ ທຳ ອິດຖືກ ນຳ ສະ ເໜີ ໃນປີ 1987, ແລະລະບົບຕ່າງໆໃນຄອບຄົວ Archimedes ໄດ້ຖືກຂາຍຈົນເຖິງກາງຊຸມປີ 1990.
Archimedes ຫມາກ: Acorn Archimedes ແມ່ນຄອບຄົວຄອມພິວເຕີສ່ວນບຸກຄົນທີ່ຖືກອອກແບບໂດຍ Acorn Computers ຂອງ Cambridge, ປະເທດອັງກິດ. ລະບົບດັ່ງກ່າວແມ່ນອີງໃສ່ໂປແກຼມສະຖາປັດຕະຍະ ກຳ ARM ຂອງ Acorn ເອງແລະລະບົບປະຕິບັດການທີ່ເປັນເຈົ້າຂອງ Arthur ແລະ RISC OS. ຮູບແບບ ທຳ ອິດຖືກ ນຳ ສະ ເໜີ ໃນປີ 1987, ແລະລະບົບຕ່າງໆໃນຄອບຄົວ Archimedes ໄດ້ຖືກຂາຍຈົນເຖິງກາງຊຸມປີ 1990.
Archimedes (crater): ອາຄານ Archimedes ແມ່ນກະດານຂະ ໜາດ ໃຫຍ່ທີ່ມີຜົນກະທົບຕາມຈັນທະເລຢູ່ແຄມຝັ່ງທາງຕາເວັນອອກຂອງ Mare Imbrium. ເສັ້ນຜ່າສູນກາງຂອງມັນແມ່ນ 81 ກມ.
Archimedes (disambiguation): Archimedes ແມ່ນນັກວິຊາຄະນິດສາດແລະນັກວິສະວະກອນຂອງປະເທດເກຣັກບູຮານ.
Archimedes (bryozoan): Archimedes ແມ່ນສະກຸນຂອງ bryozoans ທີ່ເປັນຂອງຄອບຄົວ Fenestellidae. ການ ນຳ ໃຊ້ ຄຳ ສັບທີ່ມີຊື່ວ່າ Archimedes ຄັ້ງ ທຳ ອິດໃນປີ 1838.
Archimedes (ເຮືອ): ເຮືອຫລາຍ ລຳ ໄດ້ຖືກຕັ້ງຊື່ວ່າ Archimedes ສຳ ລັບ Archimedes: Archimedes (1797) ຖືກເປີດຕົວຢູ່ Sunderland. ນາງໄດ້ຊື້ຂາຍລະຫວ່າງອັງກິດແລະ Baltic ຈົນກ່ວາລັດຖະບານອັງກິດປະຕິບັດນາງເປັນການຂົນສົ່ງ c.1809. ນາງໄດ້ສູນເສຍໄປໃນເດືອນທັນວາ 1811 ໃນຂະນະທີ່ກັບມາຈາກບານຕິກ. SS Archimedes ແມ່ນເຮືອຜະລິດອາຍນ້ ຳ ທີ່ຜະລິດຢູ່ປະເທດອັງກິດໃນປີ 1839, ແລະເຄື່ອງຈັກຜະລິດອາຍນ້ ຳ ແບບ ທຳ ອິດຂອງໂລກທີ່ຖືກຂັບເຄື່ອນໂດຍ ໝໍ້ ພັບ. SS Archimedes (1859) , ຂອງ 1,086 GRT, ຖືກສ້າງຂຶ້ນໂດຍ Palmer Bros. & CO., Newcastle upon Tyne. ໃນປີ 1867 ແລະ 1868 ນາງໄດ້ວາງສາຍໂທລະເລກລະຫວ່າງດານມາກແລະນໍເວແລະເດນມາກແລະອັງກິດ. ເຮືອ Archimedes (ປີ 1911) , ໃນ ຈຳ ນວນ 6,869 GRT ຖືກສ້າງຂຶ້ນ ສຳ ລັບ Den Line, ຜູ້ທີ່ໃຫ້ຊື່ນາງວ່າ Den of Airlie . ໃນປີຕໍ່ໄປ, Liverpool, Brazil & River Plate Navigation ໄດ້ຊື້ນາງແລະຕັ້ງຊື່ໃຫ້ນາງວ່າ Archimedes . Admiralty ໄດ້ຮຽກຮ້ອງໃຫ້ນາງຢູ່ໃນໄລຍະ WWI ແລະນາງໄດ້ຮັບໃຊ້ເປັນເຮືອຂົນສົ່ງຈາກປີ 1914-1919. ໃນປີ 1932 ຮ້ານ Steamers Ben Line ໄດ້ຊື້ນາງແລະໄດ້ປ່ຽນຊື່ນາງວ່າ Benmacdhui . ນາງໄດ້ຕີລະເບີດຝັງດິນໃນປີ 1941 ແລະຈົມລົງໃນ Spurn Head.
Archimedes ຫມາກ: Acorn Archimedes ແມ່ນຄອບຄົວຄອມພິວເຕີສ່ວນບຸກຄົນທີ່ຖືກອອກແບບໂດຍ Acorn Computers ຂອງ Cambridge, ປະເທດອັງກິດ. ລະບົບດັ່ງກ່າວແມ່ນອີງໃສ່ໂປແກຼມສະຖາປັດຕະຍະ ກຳ ARM ຂອງ Acorn ເອງແລະລະບົບປະຕິບັດການທີ່ເປັນເຈົ້າຂອງ Arthur ແລະ RISC OS. ຮູບແບບ ທຳ ອິດຖືກ ນຳ ສະ ເໜີ ໃນປີ 1987, ແລະລະບົບຕ່າງໆໃນຄອບຄົວ Archimedes ໄດ້ຖືກຂາຍຈົນເຖິງກາງຊຸມປີ 1990.
Archimedes ຫມາກ: Acorn Archimedes ແມ່ນຄອບຄົວຄອມພິວເຕີສ່ວນບຸກຄົນທີ່ຖືກອອກແບບໂດຍ Acorn Computers ຂອງ Cambridge, ປະເທດອັງກິດ. ລະບົບດັ່ງກ່າວແມ່ນອີງໃສ່ໂປແກຼມສະຖາປັດຕະຍະ ກຳ ARM ຂອງ Acorn ເອງແລະລະບົບປະຕິບັດການທີ່ເປັນເຈົ້າຂອງ Arthur ແລະ RISC OS. ຮູບແບບ ທຳ ອິດຖືກ ນຳ ສະ ເໜີ ໃນປີ 1987, ແລະລະບົບຕ່າງໆໃນຄອບຄົວ Archimedes ໄດ້ຖືກຂາຍຈົນເຖິງກາງຊຸມປີ 1990.
Archimedes Palimpsest: The Archimedes Palimpsest ແມ່ນ parchment codex palimpsest, ໃນເບື້ອງຕົ້ນແມ່ນ ສຳ ເນົາ Byzantine Greek ຂອງການລວບລວມຂອງ Archimedes ແລະຜູ້ຂຽນອື່ນໆ. ທຸກໆຮູບພາບແລະຂໍ້ມູນຈາກການບັນທຶກສາມາດໃຊ້ໄດ້ໃນອິນເຕີເນັດທີ່ Archimedes Digital Palimpsest, ພາຍໃຕ້ Creative Commons License CC BY.
ມູນນິທິ Archimedes: ມູນນິທິ Archimedes ແມ່ນອົງການເອກະລາດທີ່ຖືກສ້າງຕັ້ງຂື້ນໂດຍລັດຖະບານ Estonian ໃນປີ 1997 ໂດຍມີຈຸດປະສົງເພື່ອປະສານງານແລະຈັດຕັ້ງປະຕິບັດບັນດາໂຄງການແລະໂຄງການລະດັບຊາດແລະຕ່າງປະເທດທີ່ແຕກຕ່າງກັນໃນດ້ານການຝຶກອົບຮົມ, ການສຶກສາ, ການຄົ້ນຄວ້າ, ການພັດທະນາເຕັກໂນໂລຢີແລະນະວັດຕະ ກຳ.
Archimedes Geo3D: Archimedes Geo3D ແມ່ນຊຸດຊອບແວ ສຳ ລັບເລຂາຄະນິດແບບເຄື່ອນໄຫວໃນສາມຂະ ໜາດ. ມັນໄດ້ຖືກປ່ອຍອອກມາໃນປະເທດເຢຍລະມັນໃນເດືອນມີນາ 2006 ແລະໄດ້ຮັບລາງວັນລັດຖະບານເຢຍລະມັນ ສຳ ລັບຊອບແວການສຶກສາດີເດັ່ນໃນປີ 2007.
ກຸ່ມ Archimedes: ກຸ່ມ Archimedes ແມ່ນອົງການສືບລັບເອກະຊົນທີ່ຕັ້ງຢູ່ Tel Aviv ເຊິ່ງໄດ້ ດຳ ເນີນການໂຄສະນາການເມືອງໂດຍໃຊ້ສື່ສັງຄົມຕັ້ງແຕ່ປີ 2017.
Archimedes: Archimedes of Syracuse ແມ່ນນັກຄະນິດສາດ, ນັກຟີຊິກ, ວິສະວະກອນ, ນັກປະດິດ, ແລະນັກດາລາສາດ. ເຖິງວ່າຈະມີລາຍລະອຽດ ໜ້ອຍ ໜຶ່ງ ກ່ຽວກັບຊີວິດຂອງລາວ, ແຕ່ລາວຖືວ່າເປັນ ໜຶ່ງ ໃນນັກວິທະຍາສາດຊັ້ນ ນຳ ໃນສະ ໄໝ ເກົ່າແກ່. ຖືວ່າເປັນນັກຄະນິດສາດທີ່ຍິ່ງໃຫຍ່ທີ່ສຸດໃນປະຫວັດສາດບູຮານ, ແລະ ໜຶ່ງ ໃນສິ່ງທີ່ຍິ່ງໃຫຍ່ທີ່ສຸດໃນທຸກເວລາ, Archimedes ໄດ້ຄາດຄະເນການຄິດໄລ່ແລະການວິເຄາະທີ່ທັນສະ ໄໝ ໂດຍການ ນຳ ໃຊ້ແນວຄວາມຄິດຂອງຂະ ໜາດ ນ້ອຍແລະວິທີການ ໝົດ ແຮງເພື່ອເອົາມາໃຊ້ແລະພິສູດຢ່າງເລິກເຊິ່ງກ່ຽວກັບທິດສະດີທິດສະດີທາງເລຂາຄະນິດ, ລວມທັງ : ພື້ນທີ່ຂອງວົງມົນ; ພື້ນທີ່ແລະບໍລິມາດຂອງພື້ນທີ່; ເນື້ອທີ່ຂອງຮູບໄຂ່; ພື້ນທີ່ພາຍໃຕ້ parabola ເປັນ; ປະລິມານຂອງສ່ວນຂອງ paraboloid ຂອງການປະຕິວັດ; ປະລິມານຂອງສ່ວນຂອງ hyperboloid ຂອງການປະຕິວັດ; ແລະພື້ນທີ່ຂອງກ້ຽວວຽນ.
Archimedes Palimpsest: The Archimedes Palimpsest ແມ່ນ parchment codex palimpsest, ໃນເບື້ອງຕົ້ນແມ່ນ ສຳ ເນົາ Byzantine Greek ຂອງການລວບລວມຂອງ Archimedes ແລະຜູ້ຂຽນອື່ນໆ. ທຸກໆຮູບພາບແລະຂໍ້ມູນຈາກການບັນທຶກສາມາດໃຊ້ໄດ້ໃນອິນເຕີເນັດທີ່ Archimedes Digital Palimpsest, ພາຍໃຕ້ Creative Commons License CC BY.
ພວກເຮົາສາມາດເຮັດໄດ້ດີກວ່າ: ພວກເຮົາສາມາດເຮັດໄດ້ດີກວ່າ ນີ້ແມ່ນການເຄື່ອນໄຫວຂັ້ນຮາກຖານຢູ່ໃນລັດ Oregon ຂອງສະຫະລັດ, ເຊິ່ງມີຈຸດປະສົງເພື່ອໃຫ້ພົນລະເມືອງແລະຜູ້ມີສ່ວນຮ່ວມເຂົ້າຮ່ວມອອກແບບລະບົບການດູແລສຸຂະພາບທີ່ "ເຮັດວຽກໄດ້ດີກວ່າ ສຳ ລັບທຸກໆຄົນ." ເປົ້າ ໝາຍ ຂອງ Kitzhaber ແມ່ນເພື່ອຊອກຫາວິທີທາງໃນການວາງເງິນທີ່ໃຊ້ໃນການຮັກສາສຸຂະພາບ, ເຊິ່ງໃນປີ 2006 ມີປະມານ 6.3 ຕື້ໂດລາໃນລັດ Oregon, ເພື່ອ ນຳ ໃຊ້ທີ່ດີກວ່າ. ໃນປີນັ້ນ, ມັນແມ່ນ ໜຶ່ງ ໃນສາມອົງກອນທີ່ໄດ້ຮັບລະດັບການສະ ໜັບ ສະ ໜູນ ທີ່ເພີ່ມຂຶ້ນຢ່າງຫຼວງຫຼາຍຈາກມູນນິທິສຸຂະພາບ Northwest; ກອງທຶນຊ່ວຍເຫຼືອລ້າຂອງຕົນລວມທັງ ໝົດ 82,000 ໂດລາ.
Archimedes Palimpsest: The Archimedes Palimpsest ແມ່ນ parchment codex palimpsest, ໃນເບື້ອງຕົ້ນແມ່ນ ສຳ ເນົາ Byzantine Greek ຂອງການລວບລວມຂອງ Archimedes ແລະຜູ້ຂຽນອື່ນໆ. ທຸກໆຮູບພາບແລະຂໍ້ມູນຈາກການບັນທຶກສາມາດໃຊ້ໄດ້ໃນອິນເຕີເນັດທີ່ Archimedes Digital Palimpsest, ພາຍໃຕ້ Creative Commons License CC BY.
ການປ່ຽນແປງຂອງແຮງດັນແບບແນວຕັ້ງ: ການປ່ຽນແປງຂອງຄວາມກົດດັນແບບແນວຕັ້ງ ແມ່ນການປ່ຽນແປງຂອງຄວາມກົດດັນທີ່ເປັນ ໜ້າ ທີ່ຂອງການສູງ. ອີງຕາມທາດແຫຼວໃນ ຄຳ ຖາມແລະສະພາບການທີ່ຖືກກ່າວເຖິງ, ມັນອາດຈະມີຄວາມແຕກຕ່າງກັນຢ່າງຫຼວງຫຼາຍໃນແຕ່ລະດ້ານຕາມລວງກວ້າງເຊັ່ນດຽວກັນ, ແລະການປ່ຽນແປງເຫຼົ່ານີ້ມີຄວາມກ່ຽວຂ້ອງໃນສະພາບການຂອງແຮງກົດດັນແລະຜົນກະທົບຂອງມັນ. ເຖິງຢ່າງໃດກໍ່ຕາມ, ການປ່ຽນແປງທາງແນວຕັ້ງແມ່ນມີຄວາມ ສຳ ຄັນເປັນພິເສດ, ຍ້ອນວ່າມັນເປັນຜົນມາຈາກການດຶງແຮງໂນ້ມຖ່ວງໃສ່ທາດແຫຼວ; ຄືກັນກັບ ສຳ ລັບນ້ ຳ ທີ່ໃຫ້ໃນລະດັບດຽວກັນ, ການຫຼຸດລົງຂອງລະດັບຄວາມສູງພາຍໃນມັນເທົ່າກັບຖັນທີ່ສູງກວ່າຂອງນ້ ຳ ໜັກ ທີ່ມີນ້ ຳ ໜັກ ລົງໃນຈຸດນັ້ນ.
Archimedes Patti: Archimedes Leonidas Attilio Patti ເປັນພັນໂທກອງພົນໃນກອງທັບສະຫະລັດອາເມລິກາແລະເປັນເຈົ້າ ໜ້າ ທີ່ຫ້ອງການບໍລິການຍຸດທະສາດທີ່ເປັນຫົວ ໜ້າ ປະຕິບັດງານຢູ່ Kunming ແລະ Hanoi ໃນປີ 1945. Patti ແມ່ນເປັນທີ່ຮູ້ຈັກວ່າໄດ້ເຮັດວຽກຢ່າງໃກ້ຊິດກັບViệt Minh ແລະHồChí Minh, ຫົວ ໜ້າ ຄະນະ. ການເຄື່ອນໄຫວເອກະລາດຂອງຫວຽດນາມແລະອະນາຄົດຂອງປະທານປະເທດພາກ ເໜືອ ຫວຽດນາມ.
ບຸກຄະລິກກະພາບ Usenet: ບຸກຄະລິກກະພາບຂອງ Usenet ແມ່ນ ບຸກຄົນທີ່ ມີຊື່ສຽງໃນອິນເຕີເນັດໂດຍສະເພາະແມ່ນບຸກຄົນທີ່ໄດ້ຮັບຄວາມນິຍົມໃນລະດັບໃດ ໜຶ່ງ ຈາກການລົງໃນ Usenet ເຊິ່ງເປັນເຄືອຂ່າຍທົ່ວໂລກຂອງຜູ້ໃຊ້ຄອມພິວເຕີທີ່ມີຫົວຂໍ້ທີ່ຫຼາກຫຼາຍເພື່ອສົນທະນາ. ນັບຕັ້ງແຕ່ໄດ້ຮັບການສ້າງຕັ້ງມາ, ສຳ ນັກຂ່າວ Usenet ໄດ້ດຶງດູດຜູ້ຄົນຢ່າງຫຼວງຫຼາຍລົງປະກາດທຸກຮູບແບບຂອງຄວາມຈິງ, ການເລົ່າເລື່ອງ, ທິດສະດີ, ຄວາມຄິດເຫັນແລະຄວາມເຊື່ອຕ່າງໆ. ໂປສເຕີໃນ Usenet ບາງຄົນໄດ້ບັນລຸຊື່ສຽງແລະຄົນດັງໃນວົງການ Usenet ຈຳ ນວນ ໜຶ່ງ ເນື່ອງຈາກຄວາມຄິດທີ່ຜິດປົກກະຕິ, ບໍ່ແມ່ນແນວຄວາມຄິດຂອງພວກເຂົາ, ຫລືຍ້ອນວ່າການຂຽນແລະການຕອບຂອງພວກເຂົາຖືກພິຈາລະນາໂດຍສະເພາະແມ່ນເລື່ອງຕະຫຼົກຫລືແປກປະຫຼາດ.
ຫຼັກການຂອງ Archimedes: ຫລັກການຂອງ Archimedes ລະ ບຸວ່າແຮງກະຕຸ້ນທີ່ຂຶ້ນໄປເທິງທີ່ຖືກປ່ອຍອອກຈາກຮ່າງກາຍທີ່ຖືກຈຸ່ມລົງໃນນໍ້າ, ບໍ່ວ່າຈະເຕັມຫຼືບາງສ່ວນ, ເທົ່າກັບນ້ ຳ ໜັກ ຂອງທາດແຫຼວທີ່ຮ່າງກາຍຍ້າຍອອກ. ຫຼັກການຂອງ Archimedes ແມ່ນກົດ ໝາຍ ຂອງຟີຊິກພື້ນຖານຕໍ່ກັບກົນຈັກນ້ ຳ. ມັນຖືກສ້າງຂື້ນໂດຍ Archimedes of Syracuse.
ສັນຕາມລວງຍາວ Archimedes: Archimedes Ridge [el. 1,585 ຟຸດ (483 ມ)] ເປັນສັນຕາມລວງຍາວໃນ North Slope Borough, Alaska, ໃນສະຫະລັດ.
Archimedes Russell: Archimedes Russell ແມ່ນສະຖາປານິກອາເມລິກາທີ່ເຄື່ອນໄຫວທີ່ສຸດໃນເຂດ Syracuse, New York.
ສະກູ Archimedes: ສະ ກູຂອງ Archimedes , ເຊິ່ງເອີ້ນກັນວ່າສະ ກູລະບາຍນ້ ຳ , ຈັກສູບ ນ້ ຳ ສະກູ ຫລືສະ ກູຂອງອີຢິບ , ແມ່ນເຄື່ອງຈັກທີ່ໃຊ້ ສຳ ລັບໂອນນ້ ຳ ຈາກຮ່າງກາຍຂອງນ້ ຳ ທີ່ຕ່ ຳ ລົງສູ່ຄອງຊົນລະປະທານ. ນໍ້າໄດ້ຖືກຈັກສູບໂດຍການຫັນ ໜ້າ ດິນທີ່ມີຮູບຮ່າງ screw ພາຍໃນທໍ່. ມັນຖືກຕັ້ງຊື່ຕາມນັກປັດຊະຍາຊາວເກຣັກ Archimedes ຜູ້ທີ່ໄດ້ບັນຍາຍມັນຄັ້ງ ທຳ ອິດປະມານ 234 ປີກ່ອນຄ. ສ. ເຄື່ອງເຈາະສະກູແມ່ນອຸປະກອນທີ່ຄ້າຍຄືກັນທີ່ສົ່ງວັດສະດຸສ່ວນໃຫຍ່ເຊັ່ນແປ້ງແລະເມັດພືດ.
Ostomachion: Ostomachion , ເຊິ່ງເອີ້ນກັນວ່າ loculus Archimedius ແລະຍັງເປັນ syntomachion , ແມ່ນສົນທິສັນຍາທາງຄະນິດສາດທີ່ມີຊື່ວ່າ Archimedes. ຜົນງານດັ່ງກ່າວໄດ້ລອດຊີວິດມາເປັນສ່ວນ ໜຶ່ງ ໃນສະບັບພາສາອາຣັບແລະ ສຳ ເນົາ, ໜັງ ສື Archimedes Palimpsest , ຂອງຕົວ ໜັງ ສືກເຣັກເກົ່າແກ່ທີ່ຜະລິດໃນຍຸກ Byzantine ຄຳ ວ່າ Ostomachion ມີຕົ້ນ ກຳ ເນີດມາຈາກພາສາກະເຣັກὈστομάχιονເຊິ່ງມີຄວາມ ໝາຍ ວ່າ "ການຕໍ່ສູ້ກັບກະດູກ", ຈາກὀστέον ( osteon ), "ກະດູກ" ແລະμάχη ( mache ), "ການຕໍ່ສູ້, ການຕໍ່ສູ້, ການຕໍ່ສູ້". ໃຫ້ສັງເກດວ່າ ໜັງ ສືໃບລານອ້າງເຖິງ ຄຳ ວ່າ " Stomachion " ເຊິ່ງເປັນການສໍ້ລາດບັງຫຼວງທີ່ປາກົດຂື້ນມາຈາກພາສາກະເຣັກເດີມ. Ausonius ໃຫ້ພວກເຮົາມີຊື່ທີ່ຖືກຕ້ອງວ່າ "Ostomachion". The Ostomachion ທີ່ລາວອະທິບາຍແມ່ນປິດສະ ໜາ ຄ້າຍຄືກັບຮູບຊົງກະຈົກແລະຖືກຫຼີ້ນບາງທີໂດຍຫຼາຍໆຄົນທີ່ມີກະດູກເຮັດ. ມັນບໍ່ເປັນທີ່ຮູ້ຈັກວ່າມີອາຍຸໃດ, ການສືບສວນທາງເລຂາຄະນິດຂອງ Archimedes ກ່ຽວກັບຕົວເລກ, ຫລືເກມ. Victorinus, Bassus Ennodius ແລະ Lucretius ໄດ້ເວົ້າກ່ຽວກັບເກມເຊັ່ນກັນ.
Trajano Archimedes: Archimedes "Archie" Trajano (1956–1977) ແມ່ນນັກເຄື່ອນໄຫວນັກສຶກສາຟິລິບປິນໃນລະຫວ່າງກົດ ໝາຍ Martial ໃນປະເທດຟີລິບປິນເຊິ່ງການເສຍຊີວິດຂອງນາງແມ່ນ Imee Marcos, ລູກສາວຂອງອະດີດນັກກົດ ໝາຍ Ferdinand Marcos.
Archimedes ແລະ Seagle: Archimedes and the Seagle (1984) ແມ່ນນະວະນິຍາຍຂອງນັກຂຽນຊາວອົດສະຕາລີ David Ireland. ມັນໄດ້ຮັບຫລຽນ ຄຳ ALS Gold ໃນປີ 1985.
ຊັບສິນ Archimedean: ໃນຄະນິດສາດແລະການວິເຄາະທີ່ບໍ່ມີຕົວຕົນ, ຊັບສິນ Archimedean , ທີ່ຕັ້ງຊື່ຕາມຊື່ຄະນິດສາດຊັ້ນສູງຂອງເກຼັກ Archimedes of Syracuse, ແມ່ນຊັບສິນທີ່ຖືກຈັດຂື້ນໂດຍໂຄງສ້າງກ່ຽວກັບພຶດຊະຄະນິດບາງຢ່າງ, ເຊັ່ນ: ກຸ່ມທີ່ມີ ຄຳ ສັ່ງຫຼືມາດຕະຖານ, ແລະທົ່ງນາ. ຄຸນສົມບັດ, ທີ່ຖືກສ້າງຂື້ນໂດຍປົກກະຕິລະບຸວ່າໃຫ້ສອງຕົວເລກ x ແລະ y , ມັນຈະມີເລກເຕັມ n ເພື່ອວ່າ nx > y . ມັນຍັງຫມາຍຄວາມວ່າຊຸດຂອງຕົວເລກທໍາມະຊາດບໍ່ໄດ້ຖືກຜູກຢູ່ຂ້າງເທິງ. ເວົ້າໂດຍຫຍໍ້, ມັນແມ່ນຊັບສົມບັດຂອງການບໍ່ມີອົງປະກອບ ນ້ອຍ ຫລື ໃຫຍ່ທີ່ ບໍ່ມີຂອບເຂດ . ມັນແມ່ນ Otto Stolz ຜູ້ທີ່ໃຫ້ຊື່ຂອງ Archimedes ຍ້ອນວ່າມັນປະກົດວ່າເປັນ Axiom V ຂອງ Archimedes ' On the Sphere ແລະກະບອກ .
ອຸໂມງໃຕ້ດິນລອຍນ້ ຳ: ອຸໂມງທາງໃຕ້ດິນລອຍ ( SFT ), ເຊິ່ງເອີ້ນກັນວ່າ ຂົວທໍ່ລອຍນໍ້າ ( SFTB ), ອຸໂມງທີ່ຖືກໂຈະ , ຫຼື ຂົວ Archimedes , ແມ່ນການອອກແບບທີ່ຖືກສະ ເໜີ ສຳ ລັບອຸໂມງທີ່ລອຍຢູ່ໃນນ້ ຳ, ສະ ໜັບ ສະ ໜູນ ໂດຍຄວາມຍາວຂອງມັນ.
ອຸໂມງໃຕ້ດິນລອຍນ້ ຳ: ອຸໂມງທາງໃຕ້ດິນລອຍ ( SFT ), ເຊິ່ງເອີ້ນກັນວ່າ ຂົວທໍ່ລອຍນໍ້າ ( SFTB ), ອຸໂມງທີ່ຖືກໂຈະ , ຫຼື ຂົວ Archimedes , ແມ່ນການອອກແບບທີ່ຖືກສະ ເໜີ ສຳ ລັບອຸໂມງທີ່ລອຍຢູ່ໃນນ້ ຳ, ສະ ໜັບ ສະ ໜູນ ໂດຍຄວາມຍາວຂອງມັນ.
ບັນຫາການລ້ຽງສັດຂອງ Archimedes: ບັນຫາການລ້ຽງສັດຂອງ Archimedes ແມ່ນເປັນປັນຫາໃນການວິເຄາະ Diophantine, ການສຶກສາສົມຜົນຂອງ polynomial ກັບວິທີແກ້ໄຂແບບເຕັມ. ເນື່ອງຈາກ Archimedes, ບັນຫາກ່ຽວຂ້ອງກັບການຄິດໄລ່ ຈຳ ນວນງົວໃນຝູງສັດພະເຈົ້າແສງຕາເວັນຈາກຂໍ້ ຈຳ ກັດທີ່ ກຳ ນົດໄວ້. ບັນຫາດັ່ງກ່າວຖືກຄົ້ນພົບໂດຍ Gotthold Ephraim Lessing ໃນ ໜັງ ສືໃບລານກເຣັກບັນຈຸບົດກະວີຂອງສີ່ສິບສີ່ເສັ້ນ, ໃນຫໍສະ ໝຸດ Herzog August ໃນWolfenbüttel, ປະເທດເຢຍລະມັນໃນປີ 1773.
Archimedes (bryozoan): Archimedes ແມ່ນສະກຸນຂອງ bryozoans ທີ່ເປັນຂອງຄອບຄົວ Fenestellidae. ການ ນຳ ໃຊ້ ຄຳ ສັບທີ່ມີຊື່ວ່າ Archimedes ຄັ້ງ ທຳ ອິດໃນປີ 1838.
Archimedes (bryozoan): Archimedes ແມ່ນສະກຸນຂອງ bryozoans ທີ່ເປັນຂອງຄອບຄົວ Fenestellidae. ການ ນຳ ໃຊ້ ຄຳ ສັບທີ່ມີຊື່ວ່າ Archimedes ຄັ້ງ ທຳ ອິດໃນປີ 1838.
Pi: ໝາຍ ເລກ π ແມ່ນເລກຄະນິດສາດຄົງທີ່. ມັນຖືກ ກຳ ນົດເປັນອັດຕາສ່ວນຂອງວົງກົມຂອງວົງກົມກັບເສັ້ນຜ່າສູນກາງຂອງມັນ, ແລະມັນຍັງມີ ຄຳ ນິຍາມທຽບເທົ່າກັນ. ມັນປະກົດຢູ່ໃນຫຼາຍສູດໃນທຸກຂົງເຂດຂອງຄະນິດສາດແລະຟີຊິກ. ການນໍາໃຊ້ເປັນທີ່ຮູ້ຈັກທໍາອິດຂອງπຈົດຫມາຍສະບັບກເຣັກເປັນຕົວແທນຂອງອັດຕາສ່ວນຂອງ circumference ວົງຂອງເສັ້ນຜ່າສູນກາງຂອງຕົນແມ່ນ by ແວວນັກຄະນິດສາດ William Jones ໃນ 1706. ມັນແມ່ນປະມານເທົ່າທຽມກັນທີ່ 3,14159. ມັນໄດ້ຖືກສະແດງໂດຍຕົວອັກສອນກະເຣັກ " π " ຕັ້ງແຕ່ກາງສະຕະວັດທີ 18, ແລະຖືກສະກົດອອກເປັນ " pi ". ມັນຍັງຖືກເອີ້ນວ່າຄົງທີ່ຂອງ Archimedes .
Archimedes (crater): ອາຄານ Archimedes ແມ່ນກະດານຂະ ໜາດ ໃຫຍ່ທີ່ມີຜົນກະທົບຕາມຈັນທະເລຢູ່ແຄມຝັ່ງທາງຕາເວັນອອກຂອງ Mare Imbrium. ເສັ້ນຜ່າສູນກາງຂອງມັນແມ່ນ 81 ກມ.
Archimedes (bryozoan): Archimedes ແມ່ນສະກຸນຂອງ bryozoans ທີ່ເປັນຂອງຄອບຄົວ Fenestellidae. ການ ນຳ ໃຊ້ ຄຳ ສັບທີ່ມີຊື່ວ່າ Archimedes ຄັ້ງ ທຳ ອິດໃນປີ 1838.
Archimedes (bryozoan): Archimedes ແມ່ນສະກຸນຂອງ bryozoans ທີ່ເປັນຂອງຄອບຄົວ Fenestellidae. ການ ນຳ ໃຊ້ ຄຳ ສັບທີ່ມີຊື່ວ່າ Archimedes ຄັ້ງ ທຳ ອິດໃນປີ 1838.
Archimedes (bryozoan): Archimedes ແມ່ນສະກຸນຂອງ bryozoans ທີ່ເປັນຂອງຄອບຄົວ Fenestellidae. ການ ນຳ ໃຊ້ ຄຳ ສັບທີ່ມີຊື່ວ່າ Archimedes ຄັ້ງ ທຳ ອິດໃນປີ 1838.
Archimedes (bryozoan): Archimedes ແມ່ນສະກຸນຂອງ bryozoans ທີ່ເປັນຂອງຄອບຄົວ Fenestellidae. ການ ນຳ ໃຊ້ ຄຳ ສັບທີ່ມີຊື່ວ່າ Archimedes ຄັ້ງ ທຳ ອິດໃນປີ 1838.
Buoyancy: Buoyancy , ຫຼື upthrust , ແມ່ນຜົນບັງຄັບໃຊ້ທີ່ຂື້ນຂື້ນຂ້າງເທິງໂດຍທາດແຫຼວທີ່ຕໍ່ຕ້ານກັບນ້ ຳ ໜັກ ຂອງວັດຖຸບາງສ່ວນຫຼືບາງສ່ວນທີ່ຝັງເລິກ. ໃນຖັນຂອງນ້ ຳ, ຄວາມກົດດັນເພີ່ມຂື້ນດ້ວຍຄວາມເລິກເຊິ່ງເປັນຜົນມາຈາກນ້ ຳ ໜັກ ຂອງນ້ ຳ ທີ່ລົ້ນ. ດັ່ງນັ້ນຄວາມກົດດັນທີ່ຢູ່ທາງລຸ່ມຂອງຖັນຂອງແຫຼວແມ່ນໃຫຍ່ກວ່າຢູ່ດ້ານເທິງຂອງຖັນ. ເຊັ່ນດຽວກັນ, ຄວາມກົດດັນຢູ່ທາງລຸ່ມຂອງວັດຖຸທີ່ຖືກຈຸ່ມລົງໃນນໍ້າຈະໃຫຍ່ກວ່າຢູ່ເທິງສຸດຂອງວັດຖຸ. ຄວາມແຕກຕ່າງຂອງຄວາມກົດດັນສົ່ງຜົນໃຫ້ມີການຂື້ນເທິງສຸດຂອງວັດຖຸ. ຂະ ໜາດ ຂອງຜົນບັງຄັບໃຊ້ແມ່ນອັດຕາສ່ວນກັບຄວາມແຕກຕ່າງຂອງຄວາມກົດດັນ, ແລະທຽບເທົ່າກັບນ້ ຳ ໜັກ ຂອງແຫຼວທີ່ຖ້າບໍ່ດັ່ງນັ້ນຈະຍຶດເອົາປະລິມານທີ່ຂົມລົງຂອງວັດຖຸເຊັ່ນ: ນ້ ຳ ທີ່ຖືກຍົກຍ້າຍ.
Archimedes (bryozoan): Archimedes ແມ່ນສະກຸນຂອງ bryozoans ທີ່ເປັນຂອງຄອບຄົວ Fenestellidae. ການ ນຳ ໃຊ້ ຄຳ ສັບທີ່ມີຊື່ວ່າ Archimedes ຄັ້ງ ທຳ ອິດໃນປີ 1838.
Archimedes (bryozoan): Archimedes ແມ່ນສະກຸນຂອງ bryozoans ທີ່ເປັນຂອງຄອບຄົວ Fenestellidae. ການ ນຳ ໃຊ້ ຄຳ ສັບທີ່ມີຊື່ວ່າ Archimedes ຄັ້ງ ທຳ ອິດໃນປີ 1838.
Archimedes (bryozoan): Archimedes ແມ່ນສະກຸນຂອງ bryozoans ທີ່ເປັນຂອງຄອບຄົວ Fenestellidae. ການ ນຳ ໃຊ້ ຄຳ ສັບທີ່ມີຊື່ວ່າ Archimedes ຄັ້ງ ທຳ ອິດໃນປີ 1838.
Archimedes (bryozoan): Archimedes ແມ່ນສະກຸນຂອງ bryozoans ທີ່ເປັນຂອງຄອບຄົວ Fenestellidae. ການ ນຳ ໃຊ້ ຄຳ ສັບທີ່ມີຊື່ວ່າ Archimedes ຄັ້ງ ທຳ ອິດໃນປີ 1838.
ໝາຍ ເລກ Archimedes: ໃນນະໂຍບາຍດ້ານນ້ ຳ viscous, ຈຳ ນວນ Archimedes ( Ar ), ແມ່ນ ຈຳ ນວນມິຕິທີ່ໃຊ້ໃນການ ກຳ ນົດການເຄື່ອນໄຫວຂອງທາດແຫຼວຍ້ອນຄວາມແຕກຕ່າງຄວາມ ໜາ ແໜ້ນ, ຕັ້ງຊື່ຕາມນັກວິທະຍາສາດແລະນັກຄະນິດສາດຊາວເກຼັກບູຮານ Archimedes.
Archimedes: Archimedes of Syracuse ແມ່ນນັກຄະນິດສາດ, ນັກຟີຊິກ, ວິສະວະກອນ, ນັກປະດິດ, ແລະນັກດາລາສາດ. ເຖິງວ່າຈະມີລາຍລະອຽດ ໜ້ອຍ ໜຶ່ງ ກ່ຽວກັບຊີວິດຂອງລາວ, ແຕ່ລາວຖືວ່າເປັນ ໜຶ່ງ ໃນນັກວິທະຍາສາດຊັ້ນ ນຳ ໃນສະ ໄໝ ເກົ່າແກ່. ຖືວ່າເປັນນັກຄະນິດສາດທີ່ຍິ່ງໃຫຍ່ທີ່ສຸດໃນປະຫວັດສາດບູຮານ, ແລະ ໜຶ່ງ ໃນສິ່ງທີ່ຍິ່ງໃຫຍ່ທີ່ສຸດໃນທຸກເວລາ, Archimedes ໄດ້ຄາດຄະເນການຄິດໄລ່ແລະການວິເຄາະທີ່ທັນສະ ໄໝ ໂດຍການ ນຳ ໃຊ້ແນວຄວາມຄິດຂອງຂະ ໜາດ ນ້ອຍແລະວິທີການ ໝົດ ແຮງເພື່ອເອົາມາໃຊ້ແລະພິສູດຢ່າງເລິກເຊິ່ງກ່ຽວກັບທິດສະດີທິດສະດີທາງເລຂາຄະນິດ, ລວມທັງ : ພື້ນທີ່ຂອງວົງມົນ; ພື້ນທີ່ແລະບໍລິມາດຂອງພື້ນທີ່; ເນື້ອທີ່ຂອງຮູບໄຂ່; ພື້ນທີ່ພາຍໃຕ້ parabola ເປັນ; ປະລິມານຂອງສ່ວນຂອງ paraboloid ຂອງການປະຕິວັດ; ປະລິມານຂອງສ່ວນຂອງ hyperboloid ຂອງການປະຕິວັດ; ແລະພື້ນທີ່ຂອງກ້ຽວວຽນ.
Archimedes ຂອງ Tralles: Archimedes of Tralles ແມ່ນນັກຂຽນແລະນັກຂຽນໄວຍາກອນຊາວກະເຣັກຜູ້ທີ່ຂຽນບົດວິຈານກ່ຽວກັບວຽກງານຂອງ Homer ແລະ Plato, ແລະຍັງເປັນວຽກງານກ່ຽວກັບກົນຈັກ. ບໍ່ມີຜົນງານໃດໆຂອງລາວທີ່ມີຊີວິດລອດມາຈົນເຖິງທຸກວັນນີ້.
Archimedes Palimpsest: The Archimedes Palimpsest ແມ່ນ parchment codex palimpsest, ໃນເບື້ອງຕົ້ນແມ່ນ ສຳ ເນົາ Byzantine Greek ຂອງການລວບລວມຂອງ Archimedes ແລະຜູ້ຂຽນອື່ນໆ. ທຸກໆຮູບພາບແລະຂໍ້ມູນຈາກການບັນທຶກສາມາດໃຊ້ໄດ້ໃນອິນເຕີເນັດທີ່ Archimedes Digital Palimpsest, ພາຍໃຕ້ Creative Commons License CC BY.
ການປ່ຽນແປງຂອງແຮງດັນແບບແນວຕັ້ງ: ການປ່ຽນແປງຂອງຄວາມກົດດັນແບບແນວຕັ້ງ ແມ່ນການປ່ຽນແປງຂອງຄວາມກົດດັນທີ່ເປັນ ໜ້າ ທີ່ຂອງການສູງ. ອີງຕາມທາດແຫຼວໃນ ຄຳ ຖາມແລະສະພາບການທີ່ຖືກກ່າວເຖິງ, ມັນອາດຈະມີຄວາມແຕກຕ່າງກັນຢ່າງຫຼວງຫຼາຍໃນແຕ່ລະດ້ານຕາມລວງກວ້າງເຊັ່ນດຽວກັນ, ແລະການປ່ຽນແປງເຫຼົ່ານີ້ມີຄວາມກ່ຽວຂ້ອງໃນສະພາບການຂອງແຮງກົດດັນແລະຜົນກະທົບຂອງມັນ. ເຖິງຢ່າງໃດກໍ່ຕາມ, ການປ່ຽນແປງທາງແນວຕັ້ງແມ່ນມີຄວາມ ສຳ ຄັນເປັນພິເສດ, ຍ້ອນວ່າມັນເປັນຜົນມາຈາກການດຶງແຮງໂນ້ມຖ່ວງໃສ່ທາດແຫຼວ; ຄືກັນກັບ ສຳ ລັບນ້ ຳ ທີ່ໃຫ້ໃນລະດັບດຽວກັນ, ການຫຼຸດລົງຂອງລະດັບຄວາມສູງພາຍໃນມັນເທົ່າກັບຖັນທີ່ສູງກວ່າຂອງນ້ ຳ ໜັກ ທີ່ມີນ້ ຳ ໜັກ ລົງໃນຈຸດນັ້ນ.
ຫຼັກການຂອງ Archimedes: ຫລັກການຂອງ Archimedes ລະ ບຸວ່າແຮງກະຕຸ້ນທີ່ຂຶ້ນໄປເທິງທີ່ຖືກປ່ອຍອອກຈາກຮ່າງກາຍທີ່ຖືກຈຸ່ມລົງໃນນໍ້າ, ບໍ່ວ່າຈະເຕັມຫຼືບາງສ່ວນ, ເທົ່າກັບນ້ ຳ ໜັກ ຂອງທາດແຫຼວທີ່ຮ່າງກາຍຍ້າຍອອກ. ຫຼັກການຂອງ Archimedes ແມ່ນກົດ ໝາຍ ຂອງຟີຊິກພື້ນຖານຕໍ່ກັບກົນຈັກນ້ ຳ. ມັນຖືກສ້າງຂື້ນໂດຍ Archimedes of Syracuse.
ຊັບສິນ Archimedean: ໃນຄະນິດສາດແລະການວິເຄາະທີ່ບໍ່ມີຕົວຕົນ, ຊັບສິນ Archimedean , ທີ່ຕັ້ງຊື່ຕາມຊື່ຄະນິດສາດຊັ້ນສູງຂອງເກຼັກ Archimedes of Syracuse, ແມ່ນຊັບສິນທີ່ຖືກຈັດຂື້ນໂດຍໂຄງສ້າງກ່ຽວກັບພຶດຊະຄະນິດບາງຢ່າງ, ເຊັ່ນ: ກຸ່ມທີ່ມີ ຄຳ ສັ່ງຫຼືມາດຕະຖານ, ແລະທົ່ງນາ. ຄຸນສົມບັດ, ທີ່ຖືກສ້າງຂື້ນໂດຍປົກກະຕິລະບຸວ່າໃຫ້ສອງຕົວເລກ x ແລະ y , ມັນຈະມີເລກເຕັມ n ເພື່ອວ່າ nx > y . ມັນຍັງຫມາຍຄວາມວ່າຊຸດຂອງຕົວເລກທໍາມະຊາດບໍ່ໄດ້ຖືກຜູກຢູ່ຂ້າງເທິງ. ເວົ້າໂດຍຫຍໍ້, ມັນແມ່ນຊັບສົມບັດຂອງການບໍ່ມີອົງປະກອບ ນ້ອຍ ຫລື ໃຫຍ່ທີ່ ບໍ່ມີຂອບເຂດ . ມັນແມ່ນ Otto Stolz ຜູ້ທີ່ໃຫ້ຊື່ຂອງ Archimedes ຍ້ອນວ່າມັນປະກົດວ່າເປັນ Axiom V ຂອງ Archimedes ' On the Sphere ແລະກະບອກ .
Archimedes (bryozoan): Archimedes ແມ່ນສະກຸນຂອງ bryozoans ທີ່ເປັນຂອງຄອບຄົວ Fenestellidae. ການ ນຳ ໃຊ້ ຄຳ ສັບທີ່ມີຊື່ວ່າ Archimedes ຄັ້ງ ທຳ ອິດໃນປີ 1838.
Pyrgulopsis archimedis: Pyrgulopsis archimedis , ທີ່ຮູ້ກັນທົ່ວໄປວ່າ archimedes pyrg , ແມ່ນສາຍພັນຂອງຫອຍນ້ ຳ ຈືດນາທີທີ່ມີຫອຍນາງລົມ, ສັດນ້ ຳ gastropod molluscs ຫຼື micromolluscs ໃນຄອບຄົວ Hydrobiidae.
Archimedes: Archimedes of Syracuse ແມ່ນນັກຄະນິດສາດ, ນັກຟີຊິກ, ວິສະວະກອນ, ນັກປະດິດ, ແລະນັກດາລາສາດ. ເຖິງວ່າຈະມີລາຍລະອຽດ ໜ້ອຍ ໜຶ່ງ ກ່ຽວກັບຊີວິດຂອງລາວ, ແຕ່ລາວຖືວ່າເປັນ ໜຶ່ງ ໃນນັກວິທະຍາສາດຊັ້ນ ນຳ ໃນສະ ໄໝ ເກົ່າແກ່. ຖືວ່າເປັນນັກຄະນິດສາດທີ່ຍິ່ງໃຫຍ່ທີ່ສຸດໃນປະຫວັດສາດບູຮານ, ແລະ ໜຶ່ງ ໃນສິ່ງທີ່ຍິ່ງໃຫຍ່ທີ່ສຸດໃນທຸກເວລາ, Archimedes ໄດ້ຄາດຄະເນການຄິດໄລ່ແລະການວິເຄາະທີ່ທັນສະ ໄໝ ໂດຍການ ນຳ ໃຊ້ແນວຄວາມຄິດຂອງຂະ ໜາດ ນ້ອຍແລະວິທີການ ໝົດ ແຮງເພື່ອເອົາມາໃຊ້ແລະພິສູດຢ່າງເລິກເຊິ່ງກ່ຽວກັບທິດສະດີທິດສະດີທາງເລຂາຄະນິດ, ລວມທັງ : ພື້ນທີ່ຂອງວົງມົນ; ພື້ນທີ່ແລະບໍລິມາດຂອງພື້ນທີ່; ເນື້ອທີ່ຂອງຮູບໄຂ່; ພື້ນທີ່ພາຍໃຕ້ parabola ເປັນ; ປະລິມານຂອງສ່ວນຂອງ paraboloid ຂອງການປະຕິວັດ; ປະລິມານຂອງສ່ວນຂອງ hyperboloid ຂອງການປະຕິວັດ; ແລະພື້ນທີ່ຂອງກ້ຽວວຽນ.
ສະກູ Archimedes: ສະ ກູຂອງ Archimedes , ເຊິ່ງເອີ້ນກັນວ່າສະ ກູລະບາຍນ້ ຳ , ຈັກສູບ ນ້ ຳ ສະກູ ຫລືສະ ກູຂອງອີຢິບ , ແມ່ນເຄື່ອງຈັກທີ່ໃຊ້ ສຳ ລັບໂອນນ້ ຳ ຈາກຮ່າງກາຍຂອງນ້ ຳ ທີ່ຕ່ ຳ ລົງສູ່ຄອງຊົນລະປະທານ. ນໍ້າໄດ້ຖືກຈັກສູບໂດຍການຫັນ ໜ້າ ດິນທີ່ມີຮູບຮ່າງ screw ພາຍໃນທໍ່. ມັນຖືກຕັ້ງຊື່ຕາມນັກປັດຊະຍາຊາວເກຣັກ Archimedes ຜູ້ທີ່ໄດ້ບັນຍາຍມັນຄັ້ງ ທຳ ອິດປະມານ 234 ປີກ່ອນຄ. ສ. ເຄື່ອງເຈາະສະກູແມ່ນອຸປະກອນທີ່ຄ້າຍຄືກັນທີ່ສົ່ງວັດສະດຸສ່ວນໃຫຍ່ເຊັ່ນແປ້ງແລະເມັດພືດ.
ກ້ຽວວຽນ Archimedean: ກ້ຽວວຽນ Archimedean ແມ່ນກ້ຽວວຽນທີ່ມີຊື່ຕາມສະກຸນ Archimedes ນັກຄະນິດສາດເຣັກໃນສະຕະວັດທີ 3 ກ່ອນຄ. ສ. ມັນແມ່ນສະຖານທີ່ທີ່ສອດຄ້ອງກັບສະຖານທີ່ຕ່າງໆຕາມການເວລາຂອງຈຸດທີ່ຍ້າຍອອກໄປຈາກຈຸດຄົງທີ່ທີ່ມີຄວາມໄວຄົງທີ່ຕາມເສັ້ນທີ່ ໝຸນ ກັບຄວາມໄວຂອງມຸມ. ເທົ່າທຽມກັນ, ໃນການປະສານງານຂົ້ວໂລກ ( r , θ ) ມັນສາມາດອະທິບາຍໄດ້ໂດຍສົມຜົນ
Archimedes (bryozoan): Archimedes ແມ່ນສະກຸນຂອງ bryozoans ທີ່ເປັນຂອງຄອບຄົວ Fenestellidae. ການ ນຳ ໃຊ້ ຄຳ ສັບທີ່ມີຊື່ວ່າ Archimedes ຄັ້ງ ທຳ ອິດໃນປີ 1838.
Archimedes (bryozoan): Archimedes ແມ່ນສະກຸນຂອງ bryozoans ທີ່ເປັນຂອງຄອບຄົວ Fenestellidae. ການ ນຳ ໃຊ້ ຄຳ ສັບທີ່ມີຊື່ວ່າ Archimedes ຄັ້ງ ທຳ ອິດໃນປີ 1838.
Archimedes (bryozoan): Archimedes ແມ່ນສະກຸນຂອງ bryozoans ທີ່ເປັນຂອງຄອບຄົວ Fenestellidae. ການ ນຳ ໃຊ້ ຄຳ ສັບທີ່ມີຊື່ວ່າ Archimedes ຄັ້ງ ທຳ ອິດໃນປີ 1838.