List of trigonometric identities, List of trigonometric identities, List of trigonometric identities

ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ມຸມ: ໃນເລຂາຄະນິດຂອງ Euclidean, ມຸມ ແມ່ນຕົວເລກທີ່ຖືກສ້າງຕັ້ງຂື້ນໂດຍສອງຄີຫຼັງ, ເອີ້ນວ່າ ສອງຂ້າງ ຂອງມຸມ, ແບ່ງປັນ ຈຸດສຸດຍອດ ທົ່ວໄປ, ເອີ້ນວ່າ vertex ຂອງມຸມ. ມຸມກໍ່ຖືກສ້າງຕັ້ງຂຶ້ນໂດຍການຕັດກັນຂອງສອງຍົນ. ເຫຼົ່ານີ້ຖືກເອີ້ນວ່າມຸມໂບດ. ເສັ້ນໂຄ້ງຕັດສອງຕົວ ກຳ ນົດເປັນມຸມ ໜຶ່ງ, ເຊິ່ງແມ່ນມຸມຂອງເສັ້ນກົງຢູ່ຈຸດຕັດກັນ. ຍົກຕົວຢ່າງ, ມຸມ spherical ສ້າງຕັ້ງຂື້ນໂດຍສອງວົງມົນທີ່ຍິ່ງໃຫຍ່ຢູ່ໃນຂອບເຂດເທົ່າກັບມຸມຂອງໂບດລະຫວ່າງເຮືອບິນທີ່ບັນຈຸວົງກົມໃຫຍ່.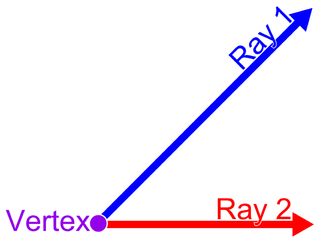
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
Angleball: Angleball ແມ່ນອົງກອນອອກ ກຳ ລັງກາຍກິລາທີ່ຈົດທະບຽນແລະເປັນຜູ້ຜະລິດອຸປະກອນທີ່ມີສິດທິບັດ ສຳ ລັບກິລາເກົ່າແກ່ທີ່ສຸດຂອງອາເມລິກາ ເໜືອ, anejodi ກົດລະບຽບຂອງ Anejodi ຂອງ Angleball ໄດ້ຖືກຈັດຕັ້ງຂື້ນ ໃໝ່ ຕາມປະເພນີຂອງຊາວອາເມລິກາໃນໄລຍະສົງຄາມໂລກຄັ້ງທີ 2 ທີ່ມະຫາວິທະຍາໄລ Brown ໂດຍວິທະຍາໄລ Hall of Fame ແລະຄູຝຶກບານບ້ວງ Charles " Rip" Engle ເພື່ອຮັກສາການບໍລິການຂອງສົງຄາມໂລກຄັ້ງທີ 2 ຂອງອາເມລິກາໃຫ້ ເໝາະ ສົມກ່ອນການປະຕິບັດງານ. ອຸປະກອນ Angleball ປະຈຸບັນມີຄົນຫຼີ້ນ 1,000,000+ ຄົນໃນສະຫະລັດແລະໃນທົ່ວໂລກແລະເພື່ອຄວາມເຢັນໃນ NFL ແລະໂດຍທີມນັກກິລາໂອລິມປິກທີມ USA. ນັບຕັ້ງແຕ່ປີ 2014, Angleball ໄດ້ສ້າງແຮງບັນດານໃຈໃຫ້ກັບເກມປະເພດເກມທີ່ຂາຍດີທີ່ສຸດໃນໂລກ, Call of Duty, ທີ່ເອີ້ນວ່າ Uplink. International Angleball ມີ 13 ປະເທດສະມາຊິກໃນປະຈຸບັນ. ອົງການ Angleball ໃຫ້ກຽດແກ່ມໍລະດົກວັດຖຸບູຮານຂອງຕົນໂດຍການຊຸກຍູ້ໃຫ້ກຸ່ມຜະລິດອຸປະກອນ anejodi ຂອງຕົນເອງເຂົ້າໃນການວັດແທກທີ່ມີສິດທິບັດຂອງ Angleball, ໂດຍ ນຳ ໃຊ້ວັດຖຸດິບທີ່ມີຢູ່ຫຼື ທຳ ມະຊາດ, ຕາບໃດທີ່ອຸປະກອນດັ່ງກ່າວບໍ່ໄດ້ຂາຍ. Angleball ແມ່ນເຄື່ອງ ໝາຍ ການຄ້າທີ່ຈົດທະບຽນແລະຖືກຂາຍໂດຍສະເພາະບໍລິສັດ Angleball.
ແຜນຜັງປາ: ໃນ ຄຳ ສັບທາງລົດໄຟ, ແຜ່ນ ປາ , ແຖບແບ່ງປັນ ຫລື ແຖບ ຮ່ວມ ແມ່ນແຖບໂລຫະທີ່ຖືກຍຶດໄປທາງປາຍຂອງລາງລົດໄຟສອງເສັ້ນເພື່ອເຂົ້າຮ່ວມພວກມັນໃນເສັ້ນທາງ. ຊື່ດັ່ງກ່າວແມ່ນມາຈາກ ປາ , ແຖບໄມ້ທີ່ມີຮູບຊົງໂຄ້ງທີ່ໃຊ້ເພື່ອສ້າງຄວາມເຂັ້ມແຂງໃຫ້ແກ່ແມ່ທັບເຮືອ. ຂອບທາງດ້ານລຸ່ມແລະທາງລຸ່ມແມ່ນ tapeed inwards ເພື່ອໃຫ້ອຸປະກອນດັ່ງກ່າວ wedges ລະຫວ່າງທາງເທິງແລະທາງລຸ່ມຂອງລາງລົດໄຟໃນເວລາທີ່ມັນຖືກ bolted ເຂົ້າໄປໃນສະຖານທີ່. ໃນການສ້າງແບບ ຈຳ ລອງການຂົນສົ່ງທາງລົດໄຟ, ປາຝາມັກຈະເປັນແຜ່ນເງິນທອງແດງຫຼືນິກເກີນນ້ອຍທີ່ເລື່ອນລົງເທິງລາງລົດໄຟທັງສອງເສັ້ນເພື່ອໃຫ້ ໜ້າ ທີ່ຂອງການຮັກສາຄວາມສອດຄ່ອງແລະການຕໍ່ໄຟຟ້າ.
ຄວາມຜິດພາດ: ໃນທາງເລຂາຄະນິດ, bisection ແມ່ນການແບ່ງບາງສິ່ງບາງຢ່າງອອກເປັນສອງສ່ວນເທົ່າກັນຫຼືເທົ່າກັນ, ຕາມປົກກະຕິໂດຍສາຍ, ເຊິ່ງຕໍ່ມາເອີ້ນວ່າ bisector . ປະເພດ bisectors ທີ່ຖືກພິຈາລະນາຫຼາຍທີ່ສຸດແມ່ນ bisector ສ່ວນ ແລະ bisector ມຸມ .
ທິດສະດີທິດສະດີກ່ຽວກັບມຸມ: ໃນເລຂາຄະນິດ, ທິດສະດີທິດສະດີມຸມຂອງ bisector ແມ່ນກ່ຽວຂ້ອງກັບຄວາມຍາວທີ່ກ່ຽວຂ້ອງຂອງສອງສ່ວນທີ່ຂ້າງຂອງສາມຫຼ່ຽມແບ່ງອອກເປັນເສັ້ນທີ່ຂີດຂ້າງມຸມກົງກັນຂ້າມ. ມັນທຽບເທົ່າກັບຄວາມຍາວຂອງພີ່ນ້ອງຂອງເຂົາເຈົ້າກັບຄວາມຍາວທີ່ກ່ຽວຂ້ອງຂອງອີກສອງຂ້າງຂອງສາມຫຼ່ຽມ.
ຄວາມຜິດພາດ: ໃນທາງເລຂາຄະນິດ, bisection ແມ່ນການແບ່ງບາງສິ່ງບາງຢ່າງອອກເປັນສອງສ່ວນເທົ່າກັນຫຼືເທົ່າກັນ, ຕາມປົກກະຕິໂດຍສາຍ, ເຊິ່ງຕໍ່ມາເອີ້ນວ່າ bisector . ປະເພດ bisectors ທີ່ຖືກພິຈາລະນາຫຼາຍທີ່ສຸດແມ່ນ bisector ສ່ວນ ແລະ bisector ມຸມ .
ວົງເລັບ: ວົງເລັບ ແມ່ນເຄື່ອງ ໝາຍ ວັກສອງອັນທີ່ມີຄວາມສູງທາງ ໜ້າ ຫລືດ້ານຫລັງທີ່ໃຊ້ທົ່ວໄປເພື່ອແຍກສ່ວນຂອງຂໍ້ຄວາມຫລືຂໍ້ມູນຈາກສິ່ງອ້ອມຂ້າງ. ການ ນຳ ໃຊ້ແບບປົກກະຕິໃນຄູ່ທີ່ມີຄວາມສອດຄ່ອງ, ວົງເລັບສ່ວນບຸກຄົນອາດຈະຖືກລະບຸວ່າເປັນວົງເລັບ ເບື້ອງຊ້າຍ ຫລື ຂວາ ຫຼືທາງເລືອກ, ວົງເລັບເປີດ ຫຼື ປິດວົງເລັບປິດ , ຕາມ ລຳ ດັບ, ຂື້ນກັບທິດທາງຂອງສະພາບການ.
ວົງເລັບມຸມ (fastener): ວົງເລັບ ຫລື ມຸມສາກມຸມ ຫລື Angle Cleat ແມ່ນເຄື່ອງຍຶດທີ່ມີຮູບຊົງ L ໃຊ້ເພື່ອເຂົ້າຮ່ວມສອງສ່ວນໂດຍທົ່ວໄປໃນມຸມ 90 ອົງສາ ປົກກະຕິແລ້ວມັນຖືກເຮັດດ້ວຍໂລຫະແຕ່ວ່າມັນຍັງສາມາດເຮັດດ້ວຍໄມ້ຫລືພາດສະຕິກໄດ້. ວົງເລັບມຸມໂລຫະມີຮູຢູ່ໃນພວກມັນ ສຳ ລັບສະກູ. ການ ນຳ ໃຊ້ແບບປົກກະຕິຂອງມັນແມ່ນການເຂົ້າໄປໃນຊັ້ນວາງໄມ້ໃສ່ຝາຫລືເຂົ້າເປັນສອງສ່ວນຂອງເຟີນີເຈີຮ່ວມກັນ
ວົງເລັບ: ວົງເລັບ ແມ່ນເຄື່ອງ ໝາຍ ວັກສອງອັນທີ່ມີຄວາມສູງທາງ ໜ້າ ຫລືດ້ານຫລັງທີ່ໃຊ້ທົ່ວໄປເພື່ອແຍກສ່ວນຂອງຂໍ້ຄວາມຫລືຂໍ້ມູນຈາກສິ່ງອ້ອມຂ້າງ. ການ ນຳ ໃຊ້ແບບປົກກະຕິໃນຄູ່ທີ່ມີຄວາມສອດຄ່ອງ, ວົງເລັບສ່ວນບຸກຄົນອາດຈະຖືກລະບຸວ່າເປັນວົງເລັບ ເບື້ອງຊ້າຍ ຫລື ຂວາ ຫຼືທາງເລືອກ, ວົງເລັບເປີດ ຫຼື ປິດວົງເລັບປິດ , ຕາມ ລຳ ດັບ, ຂື້ນກັບທິດທາງຂອງສະພາບການ.
ວົງເລັບ: ວົງເລັບ ແມ່ນເຄື່ອງ ໝາຍ ວັກສອງອັນທີ່ມີຄວາມສູງທາງ ໜ້າ ຫລືດ້ານຫລັງທີ່ໃຊ້ທົ່ວໄປເພື່ອແຍກສ່ວນຂອງຂໍ້ຄວາມຫລືຂໍ້ມູນຈາກສິ່ງອ້ອມຂ້າງ. ການ ນຳ ໃຊ້ແບບປົກກະຕິໃນຄູ່ທີ່ມີຄວາມສອດຄ່ອງ, ວົງເລັບສ່ວນບຸກຄົນອາດຈະຖືກລະບຸວ່າເປັນວົງເລັບ ເບື້ອງຊ້າຍ ຫລື ຂວາ ຫຼືທາງເລືອກ, ວົງເລັບເປີດ ຫຼື ປິດວົງເລັບປິດ , ຕາມ ລຳ ດັບ, ຂື້ນກັບທິດທາງຂອງສະພາບການ.
ລາຍຊື່ ຄຳ ສັບຄະນິດສາດ: ພາສາຂອງຄະນິດສາດມີ ຄຳ ສັບທີ່ກວ້າງຂວາງຂອງຜູ້ຊ່ຽວຊານແລະ ຄຳ ສັບທາງວິຊາການ. ມັນຍັງມີ ຈຳ ນວນ ຄຳ ສັບທີ່ແນ່ນອນ: ປະໂຫຍກທີ່ໃຊ້ກັນທົ່ວໄປເຊິ່ງເປັນສ່ວນ ໜຶ່ງ ຂອງວັດທະນະ ທຳ ຄະນິດສາດ, ຫຼາຍກວ່າຫົວຂໍ້. Jargon ມັກຈະປາກົດຢູ່ໃນການບັນຍາຍ, ແລະບາງຄັ້ງໃນການພິມ, ເປັນແບບສັ້ນໆທີ່ບໍ່ເປັນທາງການ ສຳ ລັບການໂຕ້ຖຽງທີ່ເຂັ້ມງວດຫຼືແນວຄິດທີ່ຊັດເຈນ. ຫຼາຍສິ່ງນີ້ແມ່ນພາສາອັງກິດ ທຳ ມະດາ, ແຕ່ມີຄວາມ ໝາຍ ທີ່ບໍ່ຊັດເຈນສະເພາະເມື່ອຖືກ ນຳ ໃຊ້ໃນທາງຄະນິດສາດ.
ລາຍຊື່ ຄຳ ສັບຄະນິດສາດ: ພາສາຂອງຄະນິດສາດມີ ຄຳ ສັບທີ່ກວ້າງຂວາງຂອງຜູ້ຊ່ຽວຊານແລະ ຄຳ ສັບທາງວິຊາການ. ມັນຍັງມີ ຈຳ ນວນ ຄຳ ສັບທີ່ແນ່ນອນ: ປະໂຫຍກທີ່ໃຊ້ກັນທົ່ວໄປເຊິ່ງເປັນສ່ວນ ໜຶ່ງ ຂອງວັດທະນະ ທຳ ຄະນິດສາດ, ຫຼາຍກວ່າຫົວຂໍ້. Jargon ມັກຈະປາກົດຢູ່ໃນການບັນຍາຍ, ແລະບາງຄັ້ງໃນການພິມ, ເປັນແບບສັ້ນໆທີ່ບໍ່ເປັນທາງການ ສຳ ລັບການໂຕ້ຖຽງທີ່ເຂັ້ມງວດຫຼືແນວຄິດທີ່ຊັດເຈນ. ຫຼາຍສິ່ງນີ້ແມ່ນພາສາອັງກິດ ທຳ ມະດາ, ແຕ່ມີຄວາມ ໝາຍ ທີ່ບໍ່ຊັດເຈນສະເພາະເມື່ອຖືກ ນຳ ໃຊ້ໃນທາງຄະນິດສາດ.
ພະຍາດຕາຕໍ້: ພະຍາດຕາຕໍ້ ແມ່ນກຸ່ມຂອງພະຍາດຕາເຊິ່ງສົ່ງຜົນໃຫ້ເກີດຄວາມເສຍຫາຍຕໍ່ເສັ້ນປະສາດຕາແລະເຮັດໃຫ້ສາຍຕາເສື່ອມ. ປະເພດທີ່ພົບເລື້ອຍທີ່ສຸດແມ່ນ ໂຣກຕາຕໍ້ , ໃນມຸມທີ່ລະບາຍນ້ ຳ ສຳ ລັບທາດແຫຼວພາຍໃນຕາຍັງເປີດຢູ່, ມີຊະນິດທີ່ພົບ ໜ້ອຍ ທີ່ສຸດລວມທັງພະ ຍາດຕາຕໍ້ຕຶບແລະເປັນຕາຕໍ້ ປົກກະຕິ. ພະຍາດຕາຕໍ້ເປີດຂື້ນພັດທະນາຊ້າໆຕາມເວລາແລະບໍ່ມີອາການເຈັບຫຍັງເລີຍ. ວິໄສທັດຕໍ່ພວງມະໄລອາດຈະເລີ່ມຫລຸດລົງ, ປະຕິບັດຕາມສາຍຕາກາງ, ເຮັດໃຫ້ຕາບອດຖ້າບໍ່ໄດ້ຮັບການປິ່ນປົວ. ພະຍາດຕາຕໍ້ທີ່ປິດແລ້ວສາມາດ ນຳ ສະ ເໜີ ຄ່ອຍໆຫລືກະທັນຫັນ. ການ ນຳ ສະ ເໜີ ຢ່າງກະທັນຫັນອາດຈະມີອາການເຈັບຕາຮຸນແຮງ, ມົວຕາ, ມຶນເມົາປານກາງ, ຕາແດງ, ແລະປວດຮາກ. ການສູນເສຍວິໄສທັດຈາກໂຣກຕາຕໍ້, ເມື່ອມັນເກີດຂຶ້ນ, ແມ່ນຖາວອນ. ຕາທີ່ໄດ້ຮັບຜົນກະທົບຈາກພະຍາດຕາຕໍ້ແມ່ນຖືກກ່າວເຖິງວ່າເປັນ ຕາຕໍ້ .
ພະຍາດຕາຕໍ້: ພະຍາດຕາຕໍ້ ແມ່ນກຸ່ມຂອງພະຍາດຕາເຊິ່ງສົ່ງຜົນໃຫ້ເກີດຄວາມເສຍຫາຍຕໍ່ເສັ້ນປະສາດຕາແລະເຮັດໃຫ້ສາຍຕາເສື່ອມ. ປະເພດທີ່ພົບເລື້ອຍທີ່ສຸດແມ່ນ ໂຣກຕາຕໍ້ , ໃນມຸມທີ່ລະບາຍນ້ ຳ ສຳ ລັບທາດແຫຼວພາຍໃນຕາຍັງເປີດຢູ່, ມີຊະນິດທີ່ພົບ ໜ້ອຍ ທີ່ສຸດລວມທັງພະ ຍາດຕາຕໍ້ຕຶບແລະເປັນຕາຕໍ້ ປົກກະຕິ. ພະຍາດຕາຕໍ້ເປີດຂື້ນພັດທະນາຊ້າໆຕາມເວລາແລະບໍ່ມີອາການເຈັບຫຍັງເລີຍ. ວິໄສທັດຕໍ່ພວງມະໄລອາດຈະເລີ່ມຫລຸດລົງ, ປະຕິບັດຕາມສາຍຕາກາງ, ເຮັດໃຫ້ຕາບອດຖ້າບໍ່ໄດ້ຮັບການປິ່ນປົວ. ພະຍາດຕາຕໍ້ທີ່ປິດແລ້ວສາມາດ ນຳ ສະ ເໜີ ຄ່ອຍໆຫລືກະທັນຫັນ. ການ ນຳ ສະ ເໜີ ຢ່າງກະທັນຫັນອາດຈະມີອາການເຈັບຕາຮຸນແຮງ, ມົວຕາ, ມຶນເມົາປານກາງ, ຕາແດງ, ແລະປວດຮາກ. ການສູນເສຍວິໄສທັດຈາກໂຣກຕາຕໍ້, ເມື່ອມັນເກີດຂຶ້ນ, ແມ່ນຖາວອນ. ຕາທີ່ໄດ້ຮັບຜົນກະທົບຈາກພະຍາດຕາຕໍ້ແມ່ນຖືກກ່າວເຖິງວ່າເປັນ ຕາຕໍ້ .
ສະພາບມຸມ: ໃນຄະນິດສາດ, ສະພາບມຸມ ແມ່ນຂໍ້ ຈຳ ກັດທີ່ພໍໃຈໂດຍຈຸດຊອກຫາຂອງຈຸດຕ່າງໆໃນຍົນ s ທີ່ຍົນເສົາປິດຂອງລະບົບອາໄສຢູ່. ໂດຍສົມທົບກັບສະພາບການຂະ ໜາດ, ສອງ ສຳ ນວນທາງຄະນິດສາດທັງສອງນີ້ ກຳ ນົດຮາກຖານຂອງຮາກໄດ້.
ການຫລອກລວງມຸມ: ການຫຼອກລວງມຸມ ແມ່ນເຕັກນິກການສູ້ຮົບແບບເອເລັກໂຕຣນິກທີ່ໃຊ້ເພື່ອຕ້ານກັບລະບົບເລດາສະແກນ. ມັນສ້າງສັນຍານທີ່ບໍ່ຖືກຕ້ອງເຊິ່ງເຮັດໃຫ້ radar ໂງ່ເຂົ້າໄປໃນການເຊື່ອຖືເປົ້າ ໝາຍ ແມ່ນຢູ່ເບື້ອງ ໜຶ່ງ ຂອງຄວາມໄວ, ເຊິ່ງເຮັດໃຫ້ radar" ຍ່າງ ໜີ ອອກໄປ" ຈາກເປົ້າ ໝາຍ ແລະ ທຳ ລາຍລະບົບລັອກ radar ຂອງມັນ. ມັນຍັງເປັນທີ່ຮູ້ຈັກກັນວ່າເປັນການ ຍ່າງແບບ ມຸມ , ການລັກຂະໂມຍ , ຫຼື ການສະແກນກົງກັນຂ້າມ .
ຂໍ້ບົກຜ່ອງດ້ານ Angular: ໃນທາງເລຂາຄະນິດ, ຄວາມ ບົກ ຜ່ອງດ້ານ ( ມຸມ ) ໝາຍ ເຖິງຄວາມລົ້ມເຫຼວຂອງບາງມຸມໃນການເພີ່ມປະລິມານທີ່ສູງທີ່ຄາດໄວ້ໃນ 360 °ຫຼື 180 °, ເມື່ອມຸມດັ່ງກ່າວໃນຍົນ Euclidean ຈະເປັນ. ແນວຄິດທີ່ກົງກັນຂ້າມແມ່ນເກີນ.
Autocollimator: ເຄື່ອງ ອັດສຽງອັດສະລິຍະ ແມ່ນເຄື່ອງມື optical ສຳ ລັບການວັດແທກທີ່ບໍ່ຕິດຕໍ່ຂອງມຸມ. ພວກມັນຖືກ ນຳ ໃຊ້ໂດຍປົກກະຕິເພື່ອຈັດອົງປະກອບແລະວັດແທກຄວາມບໍ່ພໍໃຈໃນລະບົບ optical ຫຼືກົນຈັກ. ເຄື່ອງອັດສຽງອັດສະລິຍະເຮັດວຽກໂດຍການຄາດຮູບພາບໃສ່ກະຈົກເປົ້າ ໝາຍ ແລະວັດແທກຄວາມຫຼົງໄຫຼຂອງຮູບພາບທີ່ກັບຄືນມາທຽບກັບລະດັບ, ບໍ່ວ່າຈະເປັນສາຍຕາຫລືໂດຍເຄື່ອງກວດເອເລັກໂຕຣນິກ. ເຄື່ອງອັດສຽງທີ່ສາມາດເບິ່ງເຫັນໄດ້ສາມາດວັດມຸມເປັນຂະ ໜາດ ນ້ອຍ 1cc ວິນາທີ, ໃນຂະນະທີ່ເຄື່ອງອັດເອເລັກໂຕຣນິກສາມາດມີຄວາມລະອຽດສູງເຖິງ 100 ເທົ່າ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
trigonometry Spherical: Spherical trigonometry ແມ່ນສາຂາຂອງເລຂາຄະນິດ spherical ທີ່ພົວພັນກັບຄວາມ ສຳ ພັນລະຫວ່າງ ໜ້າ ທີ່ຂອງ trigonometric ຂອງທັງສອງຂ້າງແລະມຸມຂອງ polygons spherical ທີ່ ກຳ ນົດໂດຍ ຈຳ ນວນວົງກົມທີ່ຕັດກັນທີ່ໃຫຍ່ໃນຂອບເຂດ. trigonometry Spherical ແມ່ນມີຄວາມ ສຳ ຄັນຫຼາຍຕໍ່ການ ຄຳ ນວນທາງດາລາສາດ, ທາງພູມສາດ, ແລະການ ນຳ ທາງ.
ຕຳ ລາໄຕມາດ: ໃນຄະນິດສາດ, ຕຳ ລາໄຕ ມາດໄຕ ມາດແມ່ນ ໜ້າ ທີ່ທີ່ແທ້ຈິງເຊິ່ງກ່ຽວຂ້ອງກັບມຸມຂອງສາມຫລ່ຽມມຸມຂວາກັບສັດສ່ວນຂອງຄວາມຍາວສອງຂ້າງ. ພວກມັນຖືກ ນຳ ໃຊ້ຢ່າງກວ້າງຂວາງໃນທຸກວິທະຍາສາດທີ່ກ່ຽວຂ້ອງກັບເລຂາຄະນິດເຊັ່ນ: ການ ນຳ ທາງ, ກົນຈັກແຂງ, ກົນຈັກຊັ້ນສູງ, ເລຂາຄະນິດແລະອື່ນໆ. ພວກມັນແມ່ນ ໜຶ່ງ ໃນບັນດາ ໜ້າ ທີ່ໃນແຕ່ລະໄລຍະທີ່ງ່າຍດາຍທີ່ສຸດ, ແລະມັນຍັງຖືກ ນຳ ໃຊ້ຢ່າງກວ້າງຂວາງໃນການສຶກສາປະກົດການແຕ່ລະໄລຍະຜ່ານການວິເຄາະ Fourier.
ຕຳ ລາໄຕມາດ: ໃນຄະນິດສາດ, ຕຳ ລາໄຕ ມາດໄຕ ມາດແມ່ນ ໜ້າ ທີ່ທີ່ແທ້ຈິງເຊິ່ງກ່ຽວຂ້ອງກັບມຸມຂອງສາມຫລ່ຽມມຸມຂວາກັບສັດສ່ວນຂອງຄວາມຍາວສອງຂ້າງ. ພວກມັນຖືກ ນຳ ໃຊ້ຢ່າງກວ້າງຂວາງໃນທຸກວິທະຍາສາດທີ່ກ່ຽວຂ້ອງກັບເລຂາຄະນິດເຊັ່ນ: ການ ນຳ ທາງ, ກົນຈັກແຂງ, ກົນຈັກຊັ້ນສູງ, ເລຂາຄະນິດແລະອື່ນໆ. ພວກມັນແມ່ນ ໜຶ່ງ ໃນບັນດາ ໜ້າ ທີ່ໃນແຕ່ລະໄລຍະທີ່ງ່າຍດາຍທີ່ສຸດ, ແລະມັນຍັງຖືກ ນຳ ໃຊ້ຢ່າງກວ້າງຂວາງໃນການສຶກສາປະກົດການແຕ່ລະໄລຍະຜ່ານການວິເຄາະ Fourier.
ໃບບິນ ສຳ ຮອງສາມຊັ້ນ: ໃບເຕີຍສາມຊັ້ນທີ່ ເອີ້ນກັນວ່າ ສາມຊັ້ນ , ແມ່ນຮູບແບບທີ່ນິຍົມຂອງ billiards carom.
ເຄື່ອງວັດມຸມ: ເຄື່ອງ ວັດແທກມຸມ ແມ່ນເຄື່ອງມືທີ່ໃຊ້ໂດຍປ່າໄມ້ເພື່ອ ກຳ ນົດວ່າຕົ້ນໄມ້ໃດທີ່ຈະວັດແທກໄດ້ໃນເວລາທີ່ ນຳ ໃຊ້ການອອກແບບດິນຕອນລັດສະ ໝີ ແບບເຄື່ອນໄຫວໃນສາງປ່າໄມ້. ການ ນຳ ໃຊ້ເຄື່ອງມືນີ້ເປັນ forester ສາມາດວັດຕົ້ນໄມ້ທີ່ຢູ່ໃນຫຼືອອກຈາກດິນຕອນ. ການວັດແທກມຸມແມ່ນຄ້າຍຄືກັບຄວາມລຽບຂອງ wedge ເຖິງແມ່ນວ່າມັນຕ້ອງໄດ້ຖືໄລຍະຫ່າງຈາກຕາເພື່ອເຮັດວຽກຢ່າງຖືກຕ້ອງ. ບໍ່ຄືກັບ prism wedge, ເຊິ່ງຖືກຈັດຢູ່ໃນສູນດິນຕອນ, ຕາຂອງຜູ້ ສຳ ຫຼວດແມ່ນຖືກເກັບຮັກສາໄວ້ ເໜືອ ຈຸດຕອນດິນຕອນທີ່ໃຊ້ເຄື່ອງວັດແທກມຸມ.
ເຄື່ອງບົດມຸມ: ເຄື່ອງຂັງມູມ , ເຊິ່ງເອີ້ນກັນວ່າເຄື່ອງບົດ ຂ້າງ ຫລື ແຜ່ນເຄື່ອງບົດ , ແມ່ນເຄື່ອງມືພະລັງງານທີ່ໃຊ້ດ້ວຍມືໃຊ້ ສຳ ລັບການປັ້ນແລະຂັດ. ເຖິງແມ່ນວ່າຖືກພັດທະນາໃນເບື້ອງຕົ້ນເປັນເຄື່ອງມື ສຳ ລັບແຜ່ນທີ່ຫຍໍ້ທີ່ແຂງກະດ້າງ, ການມີແຫຼ່ງພະລັງງານທີ່ປ່ຽນແປງໄດ້ກະຕຸ້ນໃຫ້ການ ນຳ ໃຊ້ຂອງມັນມີເຄື່ອງຕັດແລະເອກະສານຄັດຕິດຫຼາກຫຼາຍ.
Acradenia euodiiformis: Acradenia euodiiformis , ທີ່ຮູ້ກັນທົ່ວໄປວ່າຕົ້ນໄມ້ ສີເຫຼືອງ ຫຼື ໄມ້ກະດູກ , ແມ່ນຊະນິດຂອງຕົ້ນໄມ້ທີ່ ແຜ່ລາມ ໄປທາງຕາເວັນອອກຂອງອົດສະຕາລີ. ມັນສ່ວນຫຼາຍແມ່ນໃບ trifoliate, ໃບຍ່ອຍແຄບຮູບຮີແຄບຫາຮູບເປັນຮູບໄຂ່, ມີຕ່ອມນ້ ຳ ມັນທີ່ໂດດເດັ່ນ, ແລະມີດອກສີຂາວ. ມັນຈະເລີນເຕີບໂຕໃນແລະໃກ້ປ່າຝົນ.
ທິດສະດີທິດສະດີຂອງ Thales: ໃນດ້ານເລຂາຄະນິດ, ທິດສະດີທິດສະດີຂອງ Thales ລະ ບຸວ່າຖ້າ A, B, ແລະ C ແມ່ນຈຸດທີ່ແຕກຕ່າງກັນຢູ່ໃນວົງມົນບ່ອນທີ່ເສັ້ນ AC ແມ່ນເສັ້ນຜ່າສູນກາງ, ມຸມ ABC ແມ່ນມຸມຂວາ. ທິດສະດີບົດ Thales ແມ່ນເປັນກໍລະນີພິເສດຂອງທິດສະດີບົດມຸມ inscribed ແລະໄດ້ກ່າວມາແລະພິສູດເປັນສ່ວນຫນຶ່ງຂອງຂໍ້ສະເຫນີ 31 ໃນຫນັງສືສາມຂອງ Euclid ຂອງອົງປະກອບ. ໂດຍທົ່ວໄປມັນຖືກສະແດງໂດຍ Thales of Miletus ແຕ່ບາງຄັ້ງມັນກໍ່ແມ່ນຍ້ອນວ່າ Pythagoras.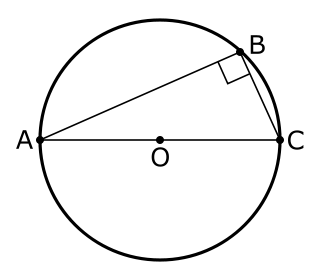
ທິດສະດີທິດສະດີຂອງ Thales: ໃນດ້ານເລຂາຄະນິດ, ທິດສະດີທິດສະດີຂອງ Thales ລະ ບຸວ່າຖ້າ A, B, ແລະ C ແມ່ນຈຸດທີ່ແຕກຕ່າງກັນຢູ່ໃນວົງມົນບ່ອນທີ່ເສັ້ນ AC ແມ່ນເສັ້ນຜ່າສູນກາງ, ມຸມ ABC ແມ່ນມຸມຂວາ. ທິດສະດີບົດ Thales ແມ່ນເປັນກໍລະນີພິເສດຂອງທິດສະດີບົດມຸມ inscribed ແລະໄດ້ກ່າວມາແລະພິສູດເປັນສ່ວນຫນຶ່ງຂອງຂໍ້ສະເຫນີ 31 ໃນຫນັງສືສາມຂອງ Euclid ຂອງອົງປະກອບ. ໂດຍທົ່ວໄປມັນຖືກສະແດງໂດຍ Thales of Miletus ແຕ່ບາງຄັ້ງມັນກໍ່ແມ່ນຍ້ອນວ່າ Pythagoras.
ນັກລົງທຶນເທວະດາ: ນັກລົງທືນທູດ ແມ່ນບຸກຄົນທີ່ສະ ໜອງ ທຶນໃຫ້ແກ່ການເລີ່ມຕົ້ນເຮັດທຸລະກິດ, ໂດຍປົກກະຕິແລ້ວແມ່ນການແລກປ່ຽນເພື່ອເປັນ ໜີ້ ທີ່ສາມາດແປງໄດ້ຫລືຮຸ້ນສ່ວນຂອງ ກຳ ມະສິດ. ນັກລົງທືນເທວະດາມັກຈະໃຫ້ການສະ ໜັບ ສະ ໜູນ ໃນການເລີ່ມຕົ້ນໃນຊ່ວງເວລາເລີ່ມຕົ້ນແລະເມື່ອນັກລົງທືນສ່ວນໃຫຍ່ບໍ່ພ້ອມທີ່ຈະສະ ໜັບ ສະ ໜູນ ພວກເຂົາ. ຈຳ ນວນນັກລົງທືນທູດ ຈຳ ນວນ ໜ້ອຍ ແຕ່ເພີ່ມຂື້ນລົງທືນ online ໂດຍຜ່ານການລົງທືນຮ່ວມທຶນຫລືຈັດຕັ້ງຕົນເອງເຂົ້າໃນ ກຸ່ມ ທູດ ຫລື ເຄືອຂ່າຍທູດ ເພື່ອແບ່ງປັນທຶນ, ພ້ອມທັງໃຫ້ ຄຳ ແນະ ນຳ ແກ່ບໍລິສັດຫຸ້ນສ່ວນຂອງພວກເຂົາ. ໃນ 50 ປີທີ່ຜ່ານມາ, ຈຳ ນວນນັກລົງທືນທູດສະຫວັນໄດ້ເພີ່ມຂື້ນຢ່າງຫຼວງຫຼາຍ.
ເຫຼັກໂຄງສ້າງ: ເຫຼັກໂຄງສ້າງ ແມ່ນ ເຫຼັກ ປະເພດ ໜຶ່ງ ທີ່ໃຊ້ ສຳ ລັບເຮັດວັດສະດຸກໍ່ສ້າງໃນຫລາຍຮູບແບບ. ຮູບຊົງເຫຼັກໂຄງສ້າງຫຼາຍຮູບແບບຂອງຮູບຊົງກະດານຍາວທີ່ມີຮູບຊົງຂອງສ່ວນຂ້າມສະເພາະ. ຮູບຊົງເຫຼັກ, ໂຄງສ້າງ, ຂະ ໜາດ, ສ່ວນປະກອບທາງເຄມີ, ຄຸນລັກສະນະກົນຈັກເຊັ່ນ: ຈຸດແຂງ, ການປະຕິບັດການເກັບຮັກສາແລະອື່ນໆແມ່ນຖືກ ກຳ ນົດຕາມມາດຕະຖານໃນປະເທດອຸດສາຫະ ກຳ ສ່ວນໃຫຍ່.
ທະເລສາບ Angle: Lake Angle ສາມາດອ້າງອີງເຖິງ: Lake Angle, Alberta, ເປັນເຂດທີ່ບໍ່ໄດ້ຮັບການແນະ ນຳ ໃນປະເທດການາດາ Lake Angle (Alberta), ທະເລສາບໃນປະເທດການາດາ ທະເລສາບ Angle ໃນ Angle Township, Lake of the Woods County, Minnesota ໃນສະຫະລັດ ທະເລສາບ Angle, Washington, ໃນ SeaTac, Washington ສະຖານີ Angle Lake, ສະຖານີຂົນສົ່ງທາງລົດໄຟໃນ SeaTac, Washington
ຕົ້ນກະຖິນ: Acacia truncata , ທີ່ຮູ້ກັນທົ່ວໄປວ່າ ມູມຝູງສັດປີກ ຫຼື ຝັ່ງທະເລທາງທິດຕາເວັນຕົກ , ເປັນໄມ້ພຸ່ມແຄມຝັ່ງທະເລໃນຄອບຄົວ Fabaceae, ມີການແຈກຢາຍພື້ນເມືອງຕາມແຄມຝັ່ງທະເລທາງທິດຕາເວັນຕົກສຽງໃຕ້ຂອງອົດສະຕາລີຕາເວັນຕົກ. ຕົວຢ່າງຂອງ wattle ນີ້ແມ່ນສ່ວນ ໜຶ່ງ ຂອງການເກັບມ້ຽນສະນະພືດສາດຂອງເອີຣົບໃນຕອນຕົ້ນ, ບາງທີອາດມາຈາກປະເທດອົດສະຕາລີ.
ຕົ້ນກະຖິນ: Acacia truncata , ທີ່ຮູ້ກັນທົ່ວໄປວ່າ ມູມຝູງສັດປີກ ຫຼື ຝັ່ງທະເລທາງທິດຕາເວັນຕົກ , ເປັນໄມ້ພຸ່ມແຄມຝັ່ງທະເລໃນຄອບຄົວ Fabaceae, ມີການແຈກຢາຍພື້ນເມືອງຕາມແຄມຝັ່ງທະເລທາງທິດຕາເວັນຕົກສຽງໃຕ້ຂອງອົດສະຕາລີຕາເວັນຕົກ. ຕົວຢ່າງຂອງ wattle ນີ້ແມ່ນສ່ວນ ໜຶ່ງ ຂອງການເກັບມ້ຽນສະນະພືດສາດຂອງເອີຣົບໃນຕອນຕົ້ນ, ບາງທີອາດມາຈາກປະເທດອົດສະຕາລີ.
ສະຖານີ Angle Lifeboat: ສະຖານີ Angle Lifeboat , Angle, Pembrokeshire, Wales, ໄດ້ເປີດເປັນຄັ້ງ ທຳ ອິດໃນປີ 1868 ຫຼັງຈາກມີການຮ້ອງຂໍຈາກ Coastguard ທ້ອງຖິ່ນ ສຳ ລັບສະຖານີຂົນສົ່ງເຮືອປະຊາຊົນທີ່ຈະເປີດພາຍໃນ Milford Haven Waterway. ເດີມເອີ້ນວ່າ ສະຖານີ Milford Lifeboat , ໃນປີ 1892 ຊື່ໄດ້ຖືກປ່ຽນແປງຢ່າງເປັນທາງການໂດຍຄະນະ ກຳ ມະການແຫ່ງຊາດ Lifeboat Institution (RNLI).
ມາດຕະການມຸມ:
ມຸມ: ໃນເລຂາຄະນິດຂອງ Euclidean, ມຸມ ແມ່ນຕົວເລກທີ່ຖືກສ້າງຕັ້ງຂື້ນໂດຍສອງຄີຫຼັງ, ເອີ້ນວ່າ ສອງຂ້າງ ຂອງມຸມ, ແບ່ງປັນ ຈຸດສຸດຍອດ ທົ່ວໄປ, ເອີ້ນວ່າ vertex ຂອງມຸມ. ມຸມກໍ່ຖືກສ້າງຕັ້ງຂຶ້ນໂດຍການຕັດກັນຂອງສອງຍົນ. ເຫຼົ່ານີ້ຖືກເອີ້ນວ່າມຸມໂບດ. ເສັ້ນໂຄ້ງຕັດສອງຕົວ ກຳ ນົດເປັນມຸມ ໜຶ່ງ, ເຊິ່ງແມ່ນມຸມຂອງເສັ້ນກົງຢູ່ຈຸດຕັດກັນ. ຍົກຕົວຢ່າງ, ມຸມ spherical ສ້າງຕັ້ງຂື້ນໂດຍສອງວົງມົນທີ່ຍິ່ງໃຫຍ່ຢູ່ໃນຂອບເຂດເທົ່າກັບມຸມຂອງໂບດລະຫວ່າງເຮືອບິນທີ່ບັນຈຸວົງກົມໃຫຍ່.
ເຄື່ອງມືວັດ: ເຄື່ອງມືວັດ ແມ່ນອຸປະກອນໃນການວັດປະລິມານທາງກາຍະພາບ. ໃນວິທະຍາສາດທາງກາຍະພາບ, ການຮັບປະກັນຄຸນນະພາບ, ແລະວິສະວະ ກຳ, ການວັດແທກແມ່ນກິດຈະ ກຳ ທີ່ໄດ້ຮັບແລະປຽບທຽບປະລິມານທາງກາຍະພາບຂອງວັດຖຸແລະເຫດການຕົວຈິງ. ວັດຖຸມາດຕະຖານແລະເຫດການທີ່ຖືກສ້າງຕັ້ງຂຶ້ນຖືກ ນຳ ໃຊ້ເປັນຫົວ ໜ່ວຍ, ແລະຂະບວນການວັດແທກເຮັດໃຫ້ຕົວເລກທີ່ກ່ຽວຂ້ອງກັບລາຍການທີ່ ກຳ ລັງສຶກສາແລະ ໜ່ວຍ ວັດແທກທີ່ອ້າງອີງ. ເຄື່ອງມືວັດ, ແລະວິທີການທົດສອບຢ່າງເປັນທາງການເຊິ່ງ ກຳ ນົດການ ນຳ ໃຊ້ເຄື່ອງມື, ແມ່ນວິທີການທີ່ການພົວພັນເຫຼົ່ານີ້ຂອງຕົວເລກໄດ້ຮັບ. ເຄື່ອງມືວັດທັງ ໝົດ ແມ່ນຂື້ນກັບລະດັບຂອງຄວາມຜິດພາດຂອງເຄື່ອງມືແລະການວັດແທກຄວາມບໍ່ແນ່ນອນ. ເຄື່ອງມືວັດນີ້ອາດຈະມີຈາກວັດຖຸທີ່ງ່າຍໆເຊັ່ນ: ໄມ້ບັນທັດແລະເສົາໄຟຟ້າຈົນເຖິງກ້ອງຈຸລະທັດແລະເຄື່ອງເລັ່ງອະນຸພາກ. ເຄື່ອງມືອຸປະກອນເສມືນຖືກ ນຳ ໃຊ້ຢ່າງກວ້າງຂວາງໃນການພັດທະນາເຄື່ອງມືວັດແທກທີ່ທັນສະ ໄໝ.
ເຄື່ອງມືວັດ: ເຄື່ອງມືວັດ ແມ່ນອຸປະກອນໃນການວັດປະລິມານທາງກາຍະພາບ. ໃນວິທະຍາສາດທາງກາຍະພາບ, ການຮັບປະກັນຄຸນນະພາບ, ແລະວິສະວະ ກຳ, ການວັດແທກແມ່ນກິດຈະ ກຳ ທີ່ໄດ້ຮັບແລະປຽບທຽບປະລິມານທາງກາຍະພາບຂອງວັດຖຸແລະເຫດການຕົວຈິງ. ວັດຖຸມາດຕະຖານແລະເຫດການທີ່ຖືກສ້າງຕັ້ງຂຶ້ນຖືກ ນຳ ໃຊ້ເປັນຫົວ ໜ່ວຍ, ແລະຂະບວນການວັດແທກເຮັດໃຫ້ຕົວເລກທີ່ກ່ຽວຂ້ອງກັບລາຍການທີ່ ກຳ ລັງສຶກສາແລະ ໜ່ວຍ ວັດແທກທີ່ອ້າງອີງ. ເຄື່ອງມືວັດ, ແລະວິທີການທົດສອບຢ່າງເປັນທາງການເຊິ່ງ ກຳ ນົດການ ນຳ ໃຊ້ເຄື່ອງມື, ແມ່ນວິທີການທີ່ການພົວພັນເຫຼົ່ານີ້ຂອງຕົວເລກໄດ້ຮັບ. ເຄື່ອງມືວັດທັງ ໝົດ ແມ່ນຂື້ນກັບລະດັບຂອງຄວາມຜິດພາດຂອງເຄື່ອງມືແລະການວັດແທກຄວາມບໍ່ແນ່ນອນ. ເຄື່ອງມືວັດນີ້ອາດຈະມີຈາກວັດຖຸທີ່ງ່າຍໆເຊັ່ນ: ໄມ້ບັນທັດແລະເສົາໄຟຟ້າຈົນເຖິງກ້ອງຈຸລະທັດແລະເຄື່ອງເລັ່ງອະນຸພາກ. ເຄື່ອງມືອຸປະກອນເສມືນຖືກ ນຳ ໃຊ້ຢ່າງກວ້າງຂວາງໃນການພັດທະນາເຄື່ອງມືວັດແທກທີ່ທັນສະ ໄໝ.
ການດັດແປງມຸມ: ການ ໝູນ ວຽນແບບມຸມ ແມ່ນຊັ້ນຮຽນຂອງການດັດສົມບັນທຸກທີ່ ນຳ ໃຊ້ໃນລະບົບສາຍສົ່ງໂທລະຄົມມະນາຄົມ. ຫ້ອງຮຽນປະກອບດ້ວຍໂມດູນຄວາມຖີ່ (FM) ແລະການປັບປ່ຽນໄລຍະ (PM), ແລະແມ່ນອີງໃສ່ການປ່ຽນແປງຄວາມຖີ່ຫລືໄລຍະຕາມ ລຳ ດັບຂອງສັນຍານຜູ້ໃຫ້ບໍລິການເພື່ອເຂົ້າລະຫັດສັນຍານຂໍ້ຄວາມ. ນີ້ກົງກັນຂ້າມກັບຄວາມກວ້າງຂອງຄວາມແຕກຕ່າງຂອງຜູ້ຂົນສົ່ງ, ປະຕິບັດໃນການສົ່ງຕໍ່ແບບໂມດູນ (AM), ເຊິ່ງແມ່ນວິທີການປ່ຽນແປງທີ່ ສຳ ຄັນທີ່ສຸດໃນການ ນຳ ໃຊ້ວິທະຍຸກະຈາຍສຽງໃນຕອນຕົ້ນ.
ໄລຍະ: ໃນຮ່າງກາຍແລະວິສະວະກໍາ, phasor ເປັນ, ເປັນຈໍານວນສະລັບສັບຊ້ອນທີ່ເປັນຕົວແທນເປັນການທໍາງານຂອງ sinusoidal ທີ່ກວ້າງຂວາງ (A), ຄວາມຖີ່ເຊີງມຸມ (ω), ແລະໂຄງການໄລຍະທໍາອິດ (θ) ແມ່ນທີ່ໃຊ້ເວລາຄົງທີ່. ມັນກ່ຽວຂ້ອງກັບແນວຄິດທົ່ວໄປຫຼາຍກວ່າທີ່ເອີ້ນວ່າການສະແດງການວິເຄາະເຊິ່ງເຮັດໃຫ້ sinusoid ເຂົ້າໄປໃນຜະລິດຕະພັນຂອງຄົງທີ່ທີ່ສັບສົນແລະປັດໄຈ ໜຶ່ງ ຂື້ນກັບເວລາແລະຄວາມຖີ່. ຄ່າຄົງທີ່ສະລັບສັບຊ້ອນ, ຊຶ່ງຂຶ້ນຢູ່ກັບຄວາມກວ້າງຂວາງແລະໂຄງການໄລຍະ, ເປັນທີ່ຮູ້ຈັກເປັນ phasor ຫລືຄວາມກວ້າງຂວາງສະລັບສັບຊ້ອນ, ແລະ sinor ຫຼືແມ້ກະທັ້ງ complexor.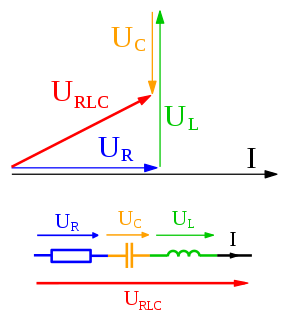
ມຸມຂອງການມາເຖິງ: ມຸມຂອງການມາເຖິງ ( AoA ) ຂອງສັນຍານແມ່ນທິດທາງທີ່ສັນຍານໄດ້ຮັບ.
ມຸມຂອງການໂຈມຕີ: ໃນນະໂຍບາຍດ້ານນ້ ຳ, ມຸມຂອງການໂຈມຕີ ແມ່ນມຸມລະຫວ່າງເສັ້ນອ້າງອີງຢູ່ໃນຮ່າງກາຍແລະ vector ທີ່ເປັນຕົວແທນໃຫ້ມີການເຄື່ອນໄຫວທີ່ກ່ຽວຂ້ອງລະຫວ່າງຮ່າງກາຍແລະນ້ ຳ ທີ່ຜ່ານການເຄື່ອນຍ້າຍຂອງມັນ. ມຸມຂອງການໂຈມຕີແມ່ນມຸມລະຫວ່າງເສັ້ນອ້າງອີງຂອງຮ່າງກາຍແລະການໄຫຼວຽນທີ່ ກຳ ລັງຈະມາ. ບົດຂຽນນີ້ສຸມໃສ່ການ ນຳ ໃຊ້ທົ່ວໄປທີ່ສຸດ, ມຸມຂອງການໂຈມຕີຂອງປີກຫລືເຮືອບິນທີ່ເຄື່ອນຍ້າຍຜ່ານທາງອາກາດ.
ມຸມຂອງການຂຶ້ນ: ໃນດ້ານອາວະກາດ, ການ ປີນພູ ແມ່ນອັດຕາສ່ວນລະຫວ່າງໄລຍະທາງທີ່ເດີນທາງ ເໜືອ ໜ້າ ດິນແລະຄວາມສູງທີ່ໄດ້ຮັບ, ແລະສະແດງເປັນເປີເຊັນ. ມຸມຂອງການປີນພູ ສາມາດຖືກ ກຳ ນົດເປັນມຸມລະຫວ່າງຍົນແນວນອນທີ່ເປັນຕົວແທນຂອງໂລກແລະເສັ້ນທາງການບິນທີ່ແທ້ຈິງຕິດຕາມມາດ້ວຍເຮືອບິນໃນລະຫວ່າງການຂຶ້ນຂອງມັນ.
ມຸມຂອງການເຂົ້າ: Angle of Entry ແມ່ນອາລະບ້ ຳ ສຽງທີ່ມີຊີວິດ ຈຳ ກັດທີ່ບັນທຶກໂດຍ Mutton Birds ໃນຊ່ວງປີ 1997 Envy of Angels UK ການທ່ອງທ່ຽວຂອງພວກເຂົາແລະປ່ອຍອອກມາໃນປ້າຍຂອງຜູ້ຈັດການຂອງພວກເຂົາ. ມັນຖືກຂາຍຢູ່ gigs ແລະໃນອິນເຕີເນັດ.
ມຸມຂອງພຣະອົງ: ມຸມຂອງພຣະອົງ , ທີ່ເອີ້ນກັນວ່າ ມຸມຂອງ esophagogastric , ແມ່ນມຸມສ້ວຍແຫຼມທີ່ຖືກສ້າງຂື້ນລະຫວ່າງ cardia ຢູ່ທາງເຂົ້າຂອງກະເພາະອາຫານ, ແລະທໍ່ອາຫານ. ມັນຊ່ວຍປ້ອງກັນການລະລາຍຂອງກົດໃນກະເພາະອາຫານເຂົ້າໄປໃນຫລອດອາຫານ. ມັນມັກຈະພັດທະນາໃນເດັກອ່ອນ, ເຮັດໃຫ້ການລະງັບອາຊິດມີຢູ່ທົ່ວໄປ.
ມຸມຂອງເຫດການ: ມຸມຂອງເຫດການ ແມ່ນມາດຕະການຂອງການເອົາໃຈໃສ່ບາງສິ່ງບາງຢ່າງຈາກ "ກົງໄປກົງມາ" ແລະອາດ ໝາຍ ເຖິງ: ມຸມຂອງການເກີດ (ອາວະກາດ), ມຸມລະຫວ່າງ chord ປີກແລະແກນຕາມລວງຍາວ, ແຕກຕ່າງຈາກມຸມຂອງການໂຈມຕີ, ເຊິ່ງກ່ຽວຂ້ອງກັບກະແສລົມ. ມຸມຂອງການເກີດ (optics), ເຊິ່ງອະທິບາຍເຖິງວິທີການຂອງກະຈົກກັບພື້ນ
ມຸມພາຍນອກ: ມຸມ sternal ແມ່ນຮ່ວມກັນ synarthrotic ສ້າງຕັ້ງຂຶ້ນໂດຍ articulation ຂອງ manubrium ແລະຮ່າງກາຍຂອງ sternum ໄດ້.
ມຸມພາຍນອກ: ມຸມ sternal ແມ່ນຮ່ວມກັນ synarthrotic ສ້າງຕັ້ງຂຶ້ນໂດຍ articulation ຂອງ manubrium ແລະຮ່າງກາຍຂອງ sternum ໄດ້.
ສະທ້ອນ (ຟີຊິກ): ການສະທ້ອນ ແມ່ນການປ່ຽນແປງທິດທາງຂອງຄື້ນຟອງໃນການໂຕ້ຕອບລະຫວ່າງສອງສື່ທີ່ແຕກຕ່າງກັນເພື່ອໃຫ້ຄື້ນຟອງກັບຄືນສູ່ສື່ກາງທີ່ມັນມີມາ. ຕົວຢ່າງ ທຳ ມະດາລວມເຖິງການສະທ້ອນແສງສະຫວ່າງ, ສຽງແລະຄື້ນຟອງນ້ ຳ. ກົດ ໝາຍ ຂອງການສະທ້ອນ ກ່າວວ່າ ສຳ ລັບການສະທ້ອນໂດຍສະເພາະມຸມທີ່ຄື້ນແມ່ນເຫດການຢູ່ເທິງ ໜ້າ ເທົ່າກັບມຸມທີ່ມັນສະທ້ອນ. ກະຈົກສະແດງການສະທ້ອນໂດຍສະເພາະ.
ກົດ ໝາຍ ຂອງ Snell: ກົດ ໝາຍ ຂອງ Snell ແມ່ນສູດທີ່ໃຊ້ເພື່ອອະທິບາຍຄວາມ ສຳ ພັນລະຫວ່າງມຸມຂອງການເກີດແລະການສະທ້ອນ, ເມື່ອກ່າວເຖິງແສງຫຼືຄື້ນອື່ນໆທີ່ຜ່ານເຂດແດນລະຫວ່າງສອງສື່ isotropic ທີ່ແຕກຕ່າງກັນ, ເຊັ່ນ: ນ້ ຳ, ແກ້ວ, ຫລືທາງອາກາດ.
ມຸມຂອງ Repose: Angle of Repose ແມ່ນນະວະນິຍາຍປີ 1971 ໂດຍ Wallace Stegner ກ່ຽວກັບນັກປະຫວັດສາດໃຊ້ລົດເຂັນ, Lyman Ward, ເຊິ່ງໄດ້ສູນເສຍສາຍ ສຳ ພັນກັບລູກຊາຍແລະຄອບຄົວທີ່ມີຊີວິດຢູ່ແລະຕັດສິນໃຈຂຽນກ່ຽວກັບປູ່ຍ່າຕາຍາຍຂອງລາວໃນເຂດແນວ ໜ້າ. ມັນໄດ້ຮັບລາງວັນວັນນະຄະດີ Pulitzer ໃນລາງວັນນິຍາຍໃນປີ 1972. ນະວະນິຍາຍແມ່ນອີງໃສ່ໂດຍກົງຈາກຕົວອັກສອນຂອງນາງ Mary Hallock Foote, ຕໍ່ມາໄດ້ຖືກພິມເຜີຍແຜ່ວ່າເປັນ ຜູ້ຍິງສຸພາບບຸລຸດໃນເຂດພາກຕາເວັນຕົກໄກ .
ມຸມຂອງ Repose: Angle of Repose ແມ່ນນະວະນິຍາຍປີ 1971 ໂດຍ Wallace Stegner ກ່ຽວກັບນັກປະຫວັດສາດໃຊ້ລົດເຂັນ, Lyman Ward, ເຊິ່ງໄດ້ສູນເສຍສາຍ ສຳ ພັນກັບລູກຊາຍແລະຄອບຄົວທີ່ມີຊີວິດຢູ່ແລະຕັດສິນໃຈຂຽນກ່ຽວກັບປູ່ຍ່າຕາຍາຍຂອງລາວໃນເຂດແນວ ໜ້າ. ມັນໄດ້ຮັບລາງວັນວັນນະຄະດີ Pulitzer ໃນລາງວັນນິຍາຍໃນປີ 1972. ນະວະນິຍາຍແມ່ນອີງໃສ່ໂດຍກົງຈາກຕົວອັກສອນຂອງນາງ Mary Hallock Foote, ຕໍ່ມາໄດ້ຖືກພິມເຜີຍແຜ່ວ່າເປັນ ຜູ້ຍິງສຸພາບບຸລຸດໃນເຂດພາກຕາເວັນຕົກໄກ .
ຂໍ້ ຈຳ ກັດຂອງສະຖຽນລະພາບໃນທາງບວກ: ຂອບເຂດ ຈຳ ກັດຂອງສະຖຽນລະພາບໃນທາງບວກ (LPS) ຫຼື ມຸມສະຖຽນລະພາບທີ່ຂາດຫາຍໄປ (AVS) ແມ່ນມຸມທີ່ຕັ້ງຈາກແນວຕັ້ງທີ່ເຮືອຈະບໍ່ຢືນຢູ່ຕໍ່ໄປອີກແລ້ວແຕ່ຈະຫມູນວຽນ, ກາຍເປັນແນວທາງ, ຫລື ໝູນ ວຽນ.
Ben Lerner: Benjamin S. Lerner ແມ່ນນັກກະວີຊາວອາເມລິກາ, ນັກຂຽນ, ນັກຂຽນ, ແລະນັກວິຈານ. ລາວໄດ້ເປັນ Fulbright Scholar, ຜູ້ສຸດທ້າຍ ສຳ ລັບລາງວັນ Pulitzer for Fiction, ຜູ້ສຸດທ້າຍ ສຳ ລັບລາງວັນປື້ມແຫ່ງຊາດ, ຜູ້ສຸດທ້າຍ ສຳ ລັບລາງວັນ Book Book Critics Circle Award, Howard Foundation Fellow, Guggenheim Fellow, ແລະ MacArthur Fellow, ແລະອື່ນໆ ກຽດຕິຍົດ. ໃນປີ 2011 ລາວໄດ້ຮັບລາງວັນ "Preis der Stadt Münsterfür internesale Poesie", ຄົນອາເມລິກາຄົນ ທຳ ອິດທີ່ໄດ້ຮັບກຽດຕິຍົດ. Lerner ສອນຢູ່ວິທະຍາໄລ Brooklyn, ບ່ອນທີ່ທ່ານໄດ້ຖືກແຕ່ງຕັ້ງໃຫ້ເປັນອາຈານສອນພາສາອັງກິດທີ່ໂດດເດັ່ນໃນປີ 2016.
ວິທີການແລະມຸມການເດີນທາງ: ມຸມເຂົ້າໃກ້ ແມ່ນ ມຸມ ສູງສຸດຂອງເສັ້ນທາງຂຶ້ນທີ່ຍານພາຫະນະສາມາດຂຶ້ນຈາກຍົນອອກຕາມແນວນອນໂດຍບໍ່ມີການແຊກແຊງ ມັນຖືກ ກຳ ນົດເປັນມຸມລະຫວ່າງພື້ນດິນແລະສາຍທີ່ຖືກກັນລະຫວ່າງຢາງລົດທາງ ໜ້າ ແລະສ່ວນທີ່ຫ້ອຍຕ່ ຳ ສຸດຂອງລົດທີ່ຈອດຢູ່ທາງ ໜ້າ. ມູມການເດີນທາງ ແມ່ນຄູ່ຂອງມັນຢູ່ດ້ານຫລັງຂອງລົດ - ມຸມສູງສຸດຈາກລົດທີ່ສາມາດລົງມາໄດ້ໂດຍບໍ່ເສຍຫາຍ. ມຸມການເຂົ້າຫາແລະການອອກເດີນທາງຍັງຖືກເອີ້ນວ່າ ມຸມທາງລາດ .
ມຸມຂອງການມາເຖິງ: ມຸມຂອງການມາເຖິງ ( AoA ) ຂອງສັນຍານແມ່ນທິດທາງທີ່ສັນຍານໄດ້ຮັບ.
ມຸມຂອງການໂຈມຕີ: ໃນນະໂຍບາຍດ້ານນ້ ຳ, ມຸມຂອງການໂຈມຕີ ແມ່ນມຸມລະຫວ່າງເສັ້ນອ້າງອີງຢູ່ໃນຮ່າງກາຍແລະ vector ທີ່ເປັນຕົວແທນໃຫ້ມີການເຄື່ອນໄຫວທີ່ກ່ຽວຂ້ອງລະຫວ່າງຮ່າງກາຍແລະນ້ ຳ ທີ່ຜ່ານການເຄື່ອນຍ້າຍຂອງມັນ. ມຸມຂອງການໂຈມຕີແມ່ນມຸມລະຫວ່າງເສັ້ນອ້າງອີງຂອງຮ່າງກາຍແລະການໄຫຼວຽນທີ່ ກຳ ລັງຈະມາ. ບົດຂຽນນີ້ສຸມໃສ່ການ ນຳ ໃຊ້ທົ່ວໄປທີ່ສຸດ, ມຸມຂອງການໂຈມຕີຂອງປີກຫລືເຮືອບິນທີ່ເຄື່ອນຍ້າຍຜ່ານທາງອາກາດ.
ມຸມຂອງການໂຈມຕີ: ໃນນະໂຍບາຍດ້ານນ້ ຳ, ມຸມຂອງການໂຈມຕີ ແມ່ນມຸມລະຫວ່າງເສັ້ນອ້າງອີງຢູ່ໃນຮ່າງກາຍແລະ vector ທີ່ເປັນຕົວແທນໃຫ້ມີການເຄື່ອນໄຫວທີ່ກ່ຽວຂ້ອງລະຫວ່າງຮ່າງກາຍແລະນ້ ຳ ທີ່ຜ່ານການເຄື່ອນຍ້າຍຂອງມັນ. ມຸມຂອງການໂຈມຕີແມ່ນມຸມລະຫວ່າງເສັ້ນອ້າງອີງຂອງຮ່າງກາຍແລະການໄຫຼວຽນທີ່ ກຳ ລັງຈະມາ. ບົດຂຽນນີ້ສຸມໃສ່ການ ນຳ ໃຊ້ທົ່ວໄປທີ່ສຸດ, ມຸມຂອງການໂຈມຕີຂອງປີກຫລືເຮືອບິນທີ່ເຄື່ອນຍ້າຍຜ່ານທາງອາກາດ.
ມຸມຂອງການໂຈມຕີ: ໃນນະໂຍບາຍດ້ານນ້ ຳ, ມຸມຂອງການໂຈມຕີ ແມ່ນມຸມລະຫວ່າງເສັ້ນອ້າງອີງຢູ່ໃນຮ່າງກາຍແລະ vector ທີ່ເປັນຕົວແທນໃຫ້ມີການເຄື່ອນໄຫວທີ່ກ່ຽວຂ້ອງລະຫວ່າງຮ່າງກາຍແລະນ້ ຳ ທີ່ຜ່ານການເຄື່ອນຍ້າຍຂອງມັນ. ມຸມຂອງການໂຈມຕີແມ່ນມຸມລະຫວ່າງເສັ້ນອ້າງອີງຂອງຮ່າງກາຍແລະການໄຫຼວຽນທີ່ ກຳ ລັງຈະມາ. ບົດຂຽນນີ້ສຸມໃສ່ການ ນຳ ໃຊ້ທົ່ວໄປທີ່ສຸດ, ມຸມຂອງການໂຈມຕີຂອງປີກຫລືເຮືອບິນທີ່ເຄື່ອນຍ້າຍຜ່ານທາງອາກາດ.
Azimuth: azimuth ແມ່ນການວັດແທກທີ່ເປັນລ່ຽມໃນລະບົບປະສານງານທາງກວ້າງ. ພາບວີດີໂອຈາກຜູ້ສັງເກດການ (ຕົ້ນ ກຳ ເນີດ) ຈົນເຖິງຈຸດທີ່ສົນໃຈແມ່ນຄາດຄະເນໄວ້ເທິງຍົນອ້າງອີງ; ມຸມລະຫວ່າງ vector ທີ່ຄາດຄະເນແລະ vector ອ້າງອີງໃສ່ຍົນອ້າງອິງເອີ້ນວ່າ azimuth.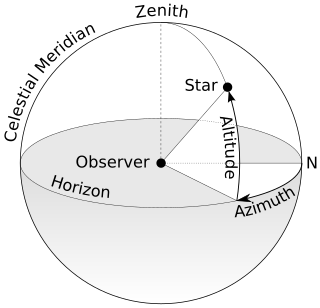
ລ້ຽວທະນາຄານ: ລ້ຽວທະນາຄານ ແມ່ນການລ້ຽວຫລືການປ່ຽນແປງທິດທາງທີ່ທະນາຄານຍານພາຫະນະຫຼືອຽງໄປຕາມປົກກະຕິ, ມັກຫັນໄປສູ່ທາງໃນ. ສຳ ລັບຖະ ໜົນ ຫລືທາງລົດໄຟນີ້ມັກເກີດຂື້ນຍ້ອນວ່າແຄມທາງມີທາງເລື່ອນລົງໄປທາງໃນຂອງເສັ້ນໂຄ້ງ. ມຸມທະນາຄານແມ່ນມຸມທີ່ຍານພາຫະນະຕິດຢູ່ຕາມລວງຍາວຂອງມັນທີ່ກ່ຽວຂ້ອງກັບແນວນອນ.
ມຸມຂອງການຂຶ້ນ: ໃນດ້ານອາວະກາດ, ການ ປີນພູ ແມ່ນອັດຕາສ່ວນລະຫວ່າງໄລຍະທາງທີ່ເດີນທາງ ເໜືອ ໜ້າ ດິນແລະຄວາມສູງທີ່ໄດ້ຮັບ, ແລະສະແດງເປັນເປີເຊັນ. ມຸມຂອງການປີນພູ ສາມາດຖືກ ກຳ ນົດເປັນມຸມລະຫວ່າງຍົນແນວນອນທີ່ເປັນຕົວແທນຂອງໂລກແລະເສັ້ນທາງການບິນທີ່ແທ້ຈິງຕິດຕາມມາດ້ວຍເຮືອບິນໃນລະຫວ່າງການຂຶ້ນຂອງມັນ.
ການປະຕິເສດ: ໃນດ້ານດາລາສາດ, ການ ຫຼຸດລົງ ແມ່ນ ໜຶ່ງ ໃນສອງມຸມທີ່ຊອກຫາຈຸດທີ່ຢູ່ໃນສະຫວັນຊັ້ນສູງໃນລະບົບປະສານງານສົມຜົນ, ອີກມຸມ ໜຶ່ງ ຊົ່ວໂມງ. ມຸມຂອງການປະກາດຖືກວັດແທກທິດ ເໜືອ ຫລືໃຕ້ຂອງເສັ້ນສູນສູດຊັ້ນສູງ, ຕາມວົງກົມຊົ່ວໂມງຜ່ານຈຸດໃນ ຄຳ ຖາມ.
ວິທີການແລະມຸມການເດີນທາງ: ມຸມເຂົ້າໃກ້ ແມ່ນ ມຸມ ສູງສຸດຂອງເສັ້ນທາງຂຶ້ນທີ່ຍານພາຫະນະສາມາດຂຶ້ນຈາກຍົນອອກຕາມແນວນອນໂດຍບໍ່ມີການແຊກແຊງ ມັນຖືກ ກຳ ນົດເປັນມຸມລະຫວ່າງພື້ນດິນແລະສາຍທີ່ຖືກກັນລະຫວ່າງຢາງລົດທາງ ໜ້າ ແລະສ່ວນທີ່ຫ້ອຍຕ່ ຳ ສຸດຂອງລົດທີ່ຈອດຢູ່ທາງ ໜ້າ. ມູມການເດີນທາງ ແມ່ນຄູ່ຂອງມັນຢູ່ດ້ານຫລັງຂອງລົດ - ມຸມສູງສຸດຈາກລົດທີ່ສາມາດລົງມາໄດ້ໂດຍບໍ່ເສຍຫາຍ. ມຸມການເຂົ້າຫາແລະການອອກເດີນທາງຍັງຖືກເອີ້ນວ່າ ມຸມທາງລາດ .
ຢຸດງານປະທ້ວງແລະຈຸ່ມ: ການໂຈມຕີແລະການອາບນ້ ຳ ໝາຍ ເຖິງການ ກຳ ນົດທິດທາງຫຼື ທັດສະນະ ຂອງຄຸນລັກສະນະທາງທໍລະນີສາດ. ເສັ້ນ ປະທ້ວງ ຂອງຕຽງນອນ, ຄວາມຜິດ, ຫລືລັກສະນະຂອງດາວເຄາະອື່ນໆ, ແມ່ນເສັ້ນທີ່ສະແດງໃຫ້ເຫັນຈຸດຕັດກັນຂອງຄຸນລັກສະນະນັ້ນດ້ວຍຍົນແນວນອນ. ໃນແຜນທີ່ດ້ານທໍລະນີສາດ, ນີ້ແມ່ນສະແດງດ້ວຍສ່ວນທີ່ສັ້ນເສັ້ນຊື່ກົງກັນກັບເສັ້ນປະທ້ວງ. ການປະທ້ວງ ສາມາດໃຫ້ໄດ້ວ່າເປັນເສັ້ນເຂັມສີ່ຫລ່ຽມຂອງເສັ້ນປະທ້ວງຫລືໃນທິດຕາເວັນອອກຫລືທິດຕາເວັນອອກສ່ຽງ ເໜືອ ຫລືໃຕ້, ຕົວເລກສາມຕົວເລກດຽວທີ່ເປັນຕົວແທນໃຫ້ azimuth, ເຊິ່ງຕົວເລກຕ່ ຳ ກວ່າປົກກະຕິແມ່ນ, ຫຼື ໝາຍ ເລກ azimuth ຕາມດ້ວຍ ໃບປະກາດລະດັບ.
ລະບົບປະສານງານ Spherical: ໃນຄະນິດສາດ, ລະບົບການປະສານງານທາງກວ້າງ ແມ່ນ ລະບົບ ປະສານງານ ສຳ ລັບພື້ນທີ່ສາມມິຕິເຊິ່ງ ຕຳ ແໜ່ງ ຈຸດໃດ ໜຶ່ງ ໄດ້ຖືກ ກຳ ນົດໂດຍສາມຕົວເລກ: ໄລຍະຫ່າງ ຂອງຈຸດນັ້ນຈາກຈຸດ ກຳ ເນີດທີ່ຄົງທີ່, ມຸມຂົ້ວ ຂອງມັນວັດຈາກທິດທາງ zenith ຄົງທີ່, ແລະ ມຸມ azimuthal ຂອງການຄາດຄະເນ orthogonal ຂອງມັນຢູ່ໃນຍົນອ້າງອີງທີ່ຜ່ານຕົ້ນ ກຳ ເນີດແລະເປັນຮູບວົງມົນໄປຫາ zenith, ວັດຈາກທິດທາງອ້າງອີງຄົງທີ່ໃນຍົນນັ້ນ. ມັນສາມາດເຫັນໄດ້ວ່າເປັນແບບສາມມິຕິຂອງລະບົບປະສານງານຂົ້ວໂລກ.
ມຸມຂອງການເຂົ້າ: Angle of Entry ແມ່ນອາລະບ້ ຳ ສຽງທີ່ມີຊີວິດ ຈຳ ກັດທີ່ບັນທຶກໂດຍ Mutton Birds ໃນຊ່ວງປີ 1997 Envy of Angels UK ການທ່ອງທ່ຽວຂອງພວກເຂົາແລະປ່ອຍອອກມາໃນປ້າຍຂອງຜູ້ຈັດການຂອງພວກເຂົາ. ມັນຖືກຂາຍຢູ່ gigs ແລະໃນອິນເຕີເນັດ.
ຄວາມແຕກແຍກ: Friction ແມ່ນຜົນບັງຄັບໃຊ້ໄດ້ resisting ການເຄື່ອນໄຫວຂອງພີ່ນ້ອງຂອງພື້ນຜິວທີ່ຫມັ້ນຄົງ, ຊັ້ນນ້ໍາ, ແລະອົງປະກອບອຸປະກອນການບໍລິການຕໍ່ກັນແລະກັນ. ການແຕກແຍກມີຫລາຍປະເພດ: ການຫົດຕົວແຫ້ງ ແມ່ນແຮງທີ່ຕ້ານກັບການເຄື່ອນໄຫວທີ່ຢູ່ທາງຂ້າງຂອງສອງ ໜ້າ ດິນທີ່ຕິດຕໍ່ກັນ. ການສັ່ນສະເທືອນແຫ້ງແມ່ນແບ່ງອອກເປັນ ການ ສັ່ນສະເທືອນ ແບບຄົງທີ່ ("stiction") ລະຫວ່າງ ໜ້າ ດິນທີ່ບໍ່ ເໜັງ ຕີງ, ແລະ ຄວາມ ຄຽດແຄ້ນຂອງ kinetic ລະຫວ່າງ ໜ້າ ທີ່ເຄື່ອນຍ້າຍ. ມີຂໍ້ຍົກເວັ້ນຂອງການປະສົມປະສານຂອງອະຕອມຫຼືໂມເລກຸນ, ການແຕກແຍກໂດຍທົ່ວໄປແມ່ນເກີດຂື້ນຈາກການປະຕິ ສຳ ພັນຂອງລັກສະນະຂອງ ໜ້າ ດິນ, ເຊິ່ງເອີ້ນວ່າ asperities. ການຫົດຕົວຂອງແຫຼວ ອະທິບາຍເຖິງການແຕກແຍກລະຫວ່າງຊັ້ນຂອງນ້ ຳ ທີ່ມີການເຄື່ອນຍ້າຍທີ່ກ່ຽວຂ້ອງກັບກັນແລະກັນ. ການລະບາຍນໍ້າມັນ Lubricated ແມ່ນກໍລະນີຂອງການຮົ່ວໄຫຼຂອງແຫຼວບ່ອນທີ່ນໍ້າມັນລໍ່ລື່ນແຍກສອງດ້ານທີ່ແຂງ. ການສຽດສີຜິວ ແມ່ນສ່ວນປະກອບຂອງການລາກ, ແຮງຕ້ານທານກັບການເຄື່ອນໄຫວຂອງທາດແຫຼວທົ່ວພື້ນຜິວຂອງຮ່າງກາຍ. ແຮງສຽດສີພາຍໃນ ແມ່ນແຮງຕ້ານທານການເຄື່ອນໄຫວລະຫວ່າງອົງປະກອບທີ່ເຮັດໃຫ້ເປັນວັດສະດຸແຂງໃນຂະນະທີ່ມັນຜ່ານການຜິດປົກກະຕິ.
ມຸມຂອງເຫດການ: ມຸມຂອງເຫດການ ແມ່ນມາດຕະການຂອງການເອົາໃຈໃສ່ບາງສິ່ງບາງຢ່າງຈາກ "ກົງໄປກົງມາ" ແລະອາດ ໝາຍ ເຖິງ: ມຸມຂອງການເກີດ (ອາວະກາດ), ມຸມລະຫວ່າງ chord ປີກແລະແກນຕາມລວງຍາວ, ແຕກຕ່າງຈາກມຸມຂອງການໂຈມຕີ, ເຊິ່ງກ່ຽວຂ້ອງກັບກະແສລົມ. ມຸມຂອງການເກີດ (optics), ເຊິ່ງອະທິບາຍເຖິງວິທີການຂອງກະຈົກກັບພື້ນ
ມຸມຂອງການເກີດ (aerodynamics): ໃນເຮືອບິນປີກທີ່ມີການສ້ອມແຊມ, ມຸມຂອງການເກີດ ແມ່ນມຸມລະຫວ່າງເສັ້ນ chord ຂອງປີກບ່ອນທີ່ປີກໄດ້ຖືກຕິດຢູ່ໃນສ່ວນຂອງ fuselage, ແລະແກນອ້າງອີງຕາມ fuselage. ມຸມຂອງການເກີດແມ່ນມີການສ້ອມແຊມໃນການອອກແບບຂອງເຮືອບິນ, ແລະມີຂໍ້ຍົກເວັ້ນທີ່ຫາຍາກ, ບໍ່ສາມາດປ່ຽນແປງໄດ້ໃນການບິນ.
ມຸມຂອງການເກີດ (aerodynamics): ໃນເຮືອບິນປີກທີ່ມີການສ້ອມແຊມ, ມຸມຂອງການເກີດ ແມ່ນມຸມລະຫວ່າງເສັ້ນ chord ຂອງປີກບ່ອນທີ່ປີກໄດ້ຖືກຕິດຢູ່ໃນສ່ວນຂອງ fuselage, ແລະແກນອ້າງອີງຕາມ fuselage. ມຸມຂອງການເກີດແມ່ນມີການສ້ອມແຊມໃນການອອກແບບຂອງເຮືອບິນ, ແລະມີຂໍ້ຍົກເວັ້ນທີ່ຫາຍາກ, ບໍ່ສາມາດປ່ຽນແປງໄດ້ໃນການບິນ.
ມຸມຂອງເຫດການ: ມຸມຂອງເຫດການ ແມ່ນມາດຕະການຂອງການເອົາໃຈໃສ່ບາງສິ່ງບາງຢ່າງຈາກ "ກົງໄປກົງມາ" ແລະອາດ ໝາຍ ເຖິງ: ມຸມຂອງການເກີດ (ອາວະກາດ), ມຸມລະຫວ່າງ chord ປີກແລະແກນຕາມລວງຍາວ, ແຕກຕ່າງຈາກມຸມຂອງການໂຈມຕີ, ເຊິ່ງກ່ຽວຂ້ອງກັບກະແສລົມ. ມຸມຂອງການເກີດ (optics), ເຊິ່ງອະທິບາຍເຖິງວິທີການຂອງກະຈົກກັບພື້ນ
ມຸມຂອງການເກີດ (optics): ໃນເລຂາຄະນິດຂອງເລຂາຄະນິດ, ມຸມຂອງການເກີດ ແມ່ນມຸມລະຫວ່າງເຫດການເລນທີ່ຢູ່ເທິງ ໜ້າ ດິນແລະເສັ້ນທາງຕັດຕໍ່ພື້ນທີ່ຈຸດເກີດເຫດ, ເອີ້ນວ່າ ທຳ ມະດາ. ຄີຫຼັງສາມາດຖືກສ້າງຕັ້ງຂື້ນໂດຍຄື້ນໃດກໍ່ຕາມ: ສາຍແສງ, ສຽງ, ສຽງ, ໄມໂຄເວຟ, X-ray ແລະອື່ນໆ ໃນຮູບຂ້າງລຸ່ມນີ້, ເສັ້ນທີ່ເປັນຕົວແທນໃຫ້ແສງສະຫວ່າງເຮັດໃຫ້ມຸມθມີປົກກະຕິ. ມຸມຂອງເຫດການທີ່ແສງສະຫວ່າງ ທຳ ອິດສະທ້ອນໃຫ້ເຫັນພາຍໃນແມ່ນເປັນມຸມທີ່ ສຳ ຄັນ. ມຸມຂອງການສະທ້ອນແລະມຸມຂອງການສະທ້ອນແມ່ນມຸມອື່ນໆທີ່ກ່ຽວຂ້ອງກັບບັນດາເສົາ.
ມຸມບັນຊີລາຍຊື່: ມຸມຂອງລາຍຊື່ ແມ່ນລະດັບທີ່ເຮືອທີ່ຈັບໃສ່ທ່າເຮືອຫລືດາວທຽມທີ່ສົມດຸນ - ໂດຍບໍ່ມີ ກຳ ລັງພາຍນອກປະຕິບັດ.
ມຸມຂອງ loll: Angle of loll ແມ່ນສະຖານະຂອງເຮືອທີ່ບໍ່ສະຖຽນລະພາບເມື່ອຖືກຕັ້ງຂື້ນແລະດັ່ງນັ້ນຈິ່ງໃຊ້ເວລາມຸມຂອງສົ້ນໃສ່ທັງທ່າເຮືອຫລືກະດານ.
ມຸມພາຍນອກ: ມຸມ sternal ແມ່ນຮ່ວມກັນ synarthrotic ສ້າງຕັ້ງຂຶ້ນໂດຍ articulation ຂອງ manubrium ແລະຮ່າງກາຍຂອງ sternum ໄດ້.
ມຸມຄວາມກົດດັນ: ມຸມຄວາມກົດດັນທີ່ ກ່ຽວຂ້ອງກັບແຂ້ວເກຍ, ທີ່ເອີ້ນກັນວ່າ ມຸມຂອງຄວາມເຄັ່ງຕຶງ , ແມ່ນມຸມລະຫວ່າງໃບ ໜ້າ ຂອງແຂ້ວແລະກົງລໍ້ເກຍ. ມັນເປັນທີ່ຊັດເຈນຫຼາຍໃນມຸມທີ່ຈຸດທີ່ມີສຽງລະຫວ່າງສາຍຂອງຄວາມກົດດັນແລະຍົນຕັ້ງຢູ່ກັບ ໜ້າ ດິນຂອງສະ ໜາມ. ມຸມຄວາມກົດດັນເຮັດໃຫ້ທິດທາງເປັນປົກກະຕິຕໍ່ຂໍ້ມູນຂອງແຂ້ວ. ມຸມຄວາມກົດດັນແມ່ນເທົ່າກັບມຸມໂປຼໄຟລ໌ທີ່ຈຸດວົງມາດຕະຖານແລະສາມາດເອີ້ນວ່າມຸມຄວາມກົດດັນ "ມາດຕະຖານ" ໃນຈຸດນັ້ນ. ຄ່າມາດຕະຖານແມ່ນ 14,5 ແລະ 20 ອົງສາ. ເຄື່ອງມືທີ່ມີແຮງດັນກ່ອນ ໜ້າ ນີ້ 14.5 ຖືກ ນຳ ໃຊ້ທົ່ວໄປເນື່ອງຈາກວ່າກາຊີນມີຂະ ໜາດ ໃຫຍ່ຂື້ນ ສຳ ລັບມຸມນ້ອຍ, ສະ ໜອງ ການສົ່ງກະແສໄຟຟ້າແລະແຮງກົດດັນ ໜ້ອຍ ລົງ; ແນວໃດກໍ່ຕາມ, ແຂ້ວທີ່ມີມຸມຄວາມດັນນ້ອຍລົງຈະອ່ອນກວ່າ. ເພື່ອແລ່ນເກຍພ້ອມກັນມຸມຄວາມກົດດັນຂອງມັນຕ້ອງຖືກຈັບຄູ່.
ມຸມຂອງຂະ ໜານ: ໃນເລຂາຄະນິດ hyperbolic, ມຸມຂອງຂະ ໜານ , ແມ່ນມູມຢູ່ມູມມຸມທີ່ບໍ່ແມ່ນມຸມຂວາຂອງສາມຫຼ່ຽມ hyperbolic ເບື້ອງຂວາມີສອງດ້ານຂະ ໜານ ກັນບ້ຽວ. ມຸມຂຶ້ນຢູ່ກັບຄວາມຍາວຕອນຫວ່າງໃນມຸມສິດແລະ vertex ຂອງມຸມຂອງຂະຫນານໄດ້.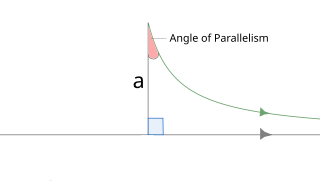
ມຸມຂອງໂບດ: ມຸມຂອງ ໂບດແມ່ນມຸມລະຫວ່າງສອງແຜນການຕັດກັນຫລືແຜນການເຄິ່ງ ໜຶ່ງ. ໃນເຄມີສາດ, ມັນແມ່ນມຸມກົງເຂັມໂມງກົງກັນຂ້າມລະຫວ່າງຍົນເຄິ່ງ ໜຶ່ງ ໂດຍຜ່ານສອງຊຸດຂອງສາມປະລໍາມະນູ, ມີສອງປະລໍາມະນູທົ່ວໄປ. ໃນເລຂາຄະນິດແຂງ, ມັນໄດ້ຖືກ ກຳ ນົດວ່າເປັນສະຫະພາບຂອງເສັ້ນແລະສອງແຜນເຄິ່ງເຄິ່ງ ໜຶ່ງ ທີ່ມີເສັ້ນນີ້ເປັນຂອບທົ່ວໄປ. ໃນຂະ ໜາດ ທີ່ສູງກວ່າ, ເສັ້ນທາງໂບດເປັນຕົວແທນໃຫ້ເຫັນລະຫວ່າງສອງຍົນ hyperplanes. ໃນເວລາທີ່ inclined ລົງພວກເຂົາເຈົ້າໄດ້ຖືກກ່າວວ່າຈະຢູ່ໃນມຸມສາດສະຫນາໃນທາງລົບ.
ມຸມຄວາມກົດດັນ: ມຸມຄວາມກົດດັນທີ່ ກ່ຽວຂ້ອງກັບແຂ້ວເກຍ, ທີ່ເອີ້ນກັນວ່າ ມຸມຂອງຄວາມເຄັ່ງຕຶງ , ແມ່ນມຸມລະຫວ່າງໃບ ໜ້າ ຂອງແຂ້ວແລະກົງລໍ້ເກຍ. ມັນເປັນທີ່ຊັດເຈນຫຼາຍໃນມຸມທີ່ຈຸດທີ່ມີສຽງລະຫວ່າງສາຍຂອງຄວາມກົດດັນແລະຍົນຕັ້ງຢູ່ກັບ ໜ້າ ດິນຂອງສະ ໜາມ. ມຸມຄວາມກົດດັນເຮັດໃຫ້ທິດທາງເປັນປົກກະຕິຕໍ່ຂໍ້ມູນຂອງແຂ້ວ. ມຸມຄວາມກົດດັນແມ່ນເທົ່າກັບມຸມໂປຼໄຟລ໌ທີ່ຈຸດວົງມາດຕະຖານແລະສາມາດເອີ້ນວ່າມຸມຄວາມກົດດັນ "ມາດຕະຖານ" ໃນຈຸດນັ້ນ. ຄ່າມາດຕະຖານແມ່ນ 14,5 ແລະ 20 ອົງສາ. ເຄື່ອງມືທີ່ມີແຮງດັນກ່ອນ ໜ້າ ນີ້ 14.5 ຖືກ ນຳ ໃຊ້ທົ່ວໄປເນື່ອງຈາກວ່າກາຊີນມີຂະ ໜາດ ໃຫຍ່ຂື້ນ ສຳ ລັບມຸມນ້ອຍ, ສະ ໜອງ ການສົ່ງກະແສໄຟຟ້າແລະແຮງກົດດັນ ໜ້ອຍ ລົງ; ແນວໃດກໍ່ຕາມ, ແຂ້ວທີ່ມີມຸມຄວາມດັນນ້ອຍລົງຈະອ່ອນກວ່າ. ເພື່ອແລ່ນເກຍພ້ອມກັນມຸມຄວາມກົດດັນຂອງມັນຕ້ອງຖືກຈັບຄູ່.
ສະທ້ອນ (ຟີຊິກ): ການສະທ້ອນ ແມ່ນການປ່ຽນແປງທິດທາງຂອງຄື້ນຟອງໃນການໂຕ້ຕອບລະຫວ່າງສອງສື່ທີ່ແຕກຕ່າງກັນເພື່ອໃຫ້ຄື້ນຟອງກັບຄືນສູ່ສື່ກາງທີ່ມັນມີມາ. ຕົວຢ່າງ ທຳ ມະດາລວມເຖິງການສະທ້ອນແສງສະຫວ່າງ, ສຽງແລະຄື້ນຟອງນ້ ຳ. ກົດ ໝາຍ ຂອງການສະທ້ອນ ກ່າວວ່າ ສຳ ລັບການສະທ້ອນໂດຍສະເພາະມຸມທີ່ຄື້ນແມ່ນເຫດການຢູ່ເທິງ ໜ້າ ເທົ່າກັບມຸມທີ່ມັນສະທ້ອນ. ກະຈົກສະແດງການສະທ້ອນໂດຍສະເພາະ.
ກົດ ໝາຍ ຂອງ Snell: ກົດ ໝາຍ ຂອງ Snell ແມ່ນສູດທີ່ໃຊ້ເພື່ອອະທິບາຍຄວາມ ສຳ ພັນລະຫວ່າງມຸມຂອງການເກີດແລະການສະທ້ອນ, ເມື່ອກ່າວເຖິງແສງຫຼືຄື້ນອື່ນໆທີ່ຜ່ານເຂດແດນລະຫວ່າງສອງສື່ isotropic ທີ່ແຕກຕ່າງກັນ, ເຊັ່ນ: ນ້ ຳ, ແກ້ວ, ຫລືທາງອາກາດ.
ມຸມຂອງ repose: ມຸມຂອງ repose , ຫຼື ມຸມທີ່ ສຳ ຄັນຂອງ repose , ຂອງວັດຖຸດິບແມ່ນມຸມທີ່ສູງທີ່ສຸດຂອງການສືບເຊື້ອສາຍຫລືອາບນ້ ຳ ທີ່ກ່ຽວຂ້ອງກັບຍົນອອກທາງນອນເຊິ່ງວັດສະດຸສາມາດຖືກປູດ້ວຍໂດຍບໍ່ຕ້ອງລອກ. ໃນມູມມອງນີ້, ວັດສະດຸຢູ່ເທິງ ໜ້າ ຜາແມ່ນຢູ່ໃກ້ໆກັບການເລື່ອນລົງ. ມຸມຂອງ repose ສາມາດຕັ້ງແຕ່ 0 °ເຖິງ 90 °. morphology ຂອງເອກະສານຜົນກະທົບຕໍ່ມຸມຂອງ repose; ເມັດຊາຍທີ່ລຽບແລະມົນບໍ່ສາມາດຖືກປູເປັນຫີນຊັນຄືກັບດິນຊາຍທີ່ຫຍາບຄາຍ. ມຸມຂອງ repose ຍັງສາມາດໄດ້ຮັບຜົນກະທົບຈາກການເພີ່ມສານລະລາຍ. ຖ້າປະລິມານນ້ ຳ ໜ້ອຍ ໜຶ່ງ ສາມາດເຊື່ອມຕໍ່ຊ່ອງຫວ່າງລະຫວ່າງອະນຸພາກ, ການດຶງດູດເອົາໄຟຟ້າຂອງນ້ ຳ ໄປສູ່ພື້ນຜິວຂອງແຮ່ທາດຈະເຮັດໃຫ້ມຸມຂອງ repose ສູງຂື້ນ, ແລະປະລິມານທີ່ກ່ຽວຂ້ອງເຊັ່ນ: ຄວາມແຂງຂອງດິນ.
ກະຕ່າໂບ: cage rib ແມ່ນການຈັດແຈງຂອງກະດູກຂ້າງຕິດກັບຄໍລໍາຂອງກະດູກສັນຫຼັງແລະ sternum ໃນ thorax ຂອງກະດູກສັນຫຼັງສ່ວນໃຫຍ່ທີ່ລ້ອມຮອບແລະປົກປ້ອງອະໄວຍະວະທີ່ ສຳ ຄັນເຊັ່ນ: ຫົວໃຈ, ປອດແລະເຮືອທີ່ຍິ່ງໃຫຍ່.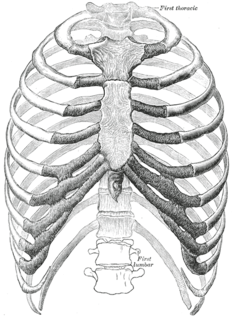
ມຸມຂອງການຫມູນວຽນ: ໃນຄະນິດສາດ, ມຸມຂອງການ ໝູນ ວຽນ ແມ່ນການວັດແທກຂອງ ຈຳ ນວນ, ຄືກັບມຸມ, ວ່າຕົວເລກຖືກ ໝູນ ວຽນປະມານຈຸດຄົງທີ່, ສ່ວນຫຼາຍແມ່ນຈຸດໃຈກາງຂອງວົງກົມ. ການຫມູນວຽນຕາມເຂັມໂມງຖືກຖືວ່າເປັນການຫມູນວຽນທາງລົບ, ສະນັ້ນ, ຕົວຢ່າງ, ການຫມູນວຽນຂອງ 310 ° (ກົງກັນຂ້າມທາງຂວາງ) ຍັງສາມາດເອີ້ນວ່າການຫມູນວຽນຂອງ –50 °. ການຫມູນວຽນຕາມທິດທາງກົງກັນຂ້າມຂອງຫຼາຍກ່ວາ ໜຶ່ງ ບາດລ້ຽວທີ່ຖືກວັດແທກໂດຍປົກກະຕິແມ່ນວັດແທກໂມເລກຸນ 360 °, ໝາຍ ຄວາມວ່າ 360 °ຖືກຫັກອອກເປັນຫຼາຍເທົ່າທີ່ຈະເປັນໄປໄດ້ທີ່ຈະປ່ອຍໃຫ້ມີການວັດແທກທີ່ບໍ່ລົບລົບຫນ້ອຍກ່ວາ 360 °.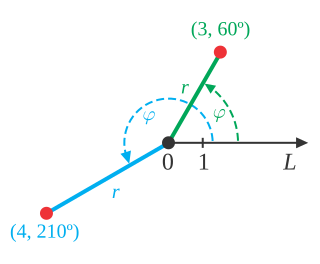
Scapula: ໃນການວິພາກວິທະຍາ, scapula , ເຊິ່ງເອີ້ນກັນວ່າ ກະດູກ ບ່າ , ແຜ່ນບ່າໄຫລ່ , ກະດູກປີກ ຫຼື ກະດູກແຜ່ນກະດູກ , ແມ່ນກະດູກທີ່ເຊື່ອມຕໍ່ humerus ກັບ clavicle. ເຊັ່ນດຽວກັນກັບກະດູກທີ່ເຊື່ອມຕໍ່ຂອງພວກມັນ, scapulae ແມ່ນມີລັກສະນະເປັນຄູ່, ເຊິ່ງແຕ່ລະ scapula ຢູ່ສອງຂ້າງຂອງຮ່າງກາຍແມ່ນຮູບກະຈົກຂອງອີກຂ້າງ ໜຶ່ງ. ຊື່ດັ່ງກ່າວໄດ້ມາຈາກ ຄຳ ນາມພາສາລາແຕັງຄລາສສິກ ສຳ ລັບຜ້າປູພື້ນຫລືຊ້ວນນ້ອຍ, ເຊິ່ງມັນໄດ້ຖືກຄິດວ່າຄ້າຍຄືກັນ.