Slip angle, Slip (aerodynamics), Anterior chamber angle

ມຸມເລື່ອນ: ໃນນະໂຍບາຍດ້ານພາຫະນະ, ມຸມເລື່ອນ ຫລື ມຸມ ຂ້າງ ແມ່ນມຸມທີ່ຢູ່ລະຫວ່າງທິດທາງທີ່ລໍ້ ກຳ ລັງຊີ້ແລະທິດທາງທີ່ມັນ ກຳ ລັງເດີນທາງ. ມຸມເລື່ອນນີ້ສົ່ງຜົນໃຫ້ເກີດມີແຮງບິດ, ແຮງດັນທີ່ຢູ່ໃນຍົນຂອງແຜ່ນຕິດຕໍ່ແລະເສັ້ນທາງຂວາງຂອງຈຸດເຊື່ອມຕໍ່ຂອງແຜ່ນຕິດຕໍ່ແລະທາງກາງຂອງລໍ້. ພະລັງງານມູມນີ້ເພີ່ມຂື້ນປະມານເສັ້ນ ສຳ ລັບສອງສາມອົງສາ ທຳ ອິດຂອງມຸມເລື່ອນ, ຫຼັງຈາກນັ້ນເພີ່ມຂື້ນທີ່ບໍ່ແມ່ນເສັ້ນເຖິງສູງສຸດກ່ອນທີ່ຈະເລີ່ມຫຼຸດລົງ.
ຄວາມຜິດພາດ (aerodynamics): ຄວາມ ຜິດພາດ ພຽງແມ່ນສະຖານະພາບທາງອາກາດເຊິ່ງເຮືອບິນ ກຳ ລັງເຄື່ອນ ທີ່ ໄປທາງຂ້າງເຊັ່ນດຽວກັນກັບໄປຂ້າງ ໜ້າ ກ່ຽວກັບກະແສລົມທີ່ ກຳ ລັງຈະມາ. ເວົ້າອີກຢ່າງ ໜຶ່ງ, ສຳ ລັບເຮືອບິນ ທຳ ມະດາ, ດັງຈະຖືກຊີ້ໄປທາງທິດທາງກົງກັນຂ້າມກັບຝັ່ງຂອງປີກ. ເຮືອບິນບໍ່ໄດ້ຢູ່ໃນຖ້ຽວບິນທີ່ປະສານງານກັນແລະດັ່ງນັ້ນຈຶ່ງບິນໄດ້ບໍ່ມີປະສິດຕິພາບ.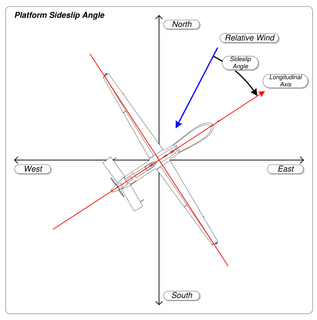
ມຸມຂອງຫ້ອງຂ້າງ ໜ້າ: ມຸມຂອງຫ້ອງຂ້າງ ໜ້າ ແມ່ນສ່ວນ ໜຶ່ງ ຂອງຕາທີ່ຕັ້ງຢູ່ລະຫວ່າງຕາແລະແກ້ວຕາທີ່ປະກອບດ້ວຍຕາຫນ່າງເຫຼັກ. ຂະ ໜາດ ຂອງມຸມນີ້ແມ່ນຕົວ ກຳ ນົດທີ່ ສຳ ຄັນຂອງອັດຕາອາລົມຕະຫລົກທີ່ຫລັ່ງໄຫລອອກຈາກສາຍຕາ, ແລະດັ່ງນັ້ນ, ຄວາມກົດດັນໃນເສັ້ນເລືອດ. ມຸມຂອງຫ້ອງສະພາຂ້າງ ໜ້າ ແມ່ນໂຄງສ້າງທີ່ ກຳ ນົດຄວາມເລິກຂອງສະພາທີ່ລ່ວງ ໜ້າ. ມຸມຂອງຫ້ອງຂ້າງແຄບທີ່ສຸດແມ່ນຄຸນລັກສະນະຂອງການປິດພະຍາດຕາຕໍ້.
ມຸມຂອງ ໜ້າ ທີ່ຮັບຜິດຊອບ: ມຸມຂອງໃບບັງຄັບ ແມ່ນຕັ້ງຢູ່ຊາຍແດນຫລັງຕິດກັນທີ່ຈຸດເຊື່ອມຕໍ່ຂອງຊາຍແດນຕ່ ຳ ຂອງ ramus ຂອງບັງຄັບ.
Scapula: ໃນການວິພາກວິທະຍາ, scapula , ເຊິ່ງເອີ້ນກັນວ່າ ກະດູກ ບ່າ , ແຜ່ນບ່າໄຫລ່ , ກະດູກປີກ ຫຼື ກະດູກແຜ່ນກະດູກ , ແມ່ນກະດູກທີ່ເຊື່ອມຕໍ່ humerus ກັບ clavicle. ເຊັ່ນດຽວກັນກັບກະດູກທີ່ເຊື່ອມຕໍ່ຂອງພວກມັນ, scapulae ແມ່ນມີລັກສະນະເປັນຄູ່, ເຊິ່ງແຕ່ລະ scapula ຢູ່ສອງຂ້າງຂອງຮ່າງກາຍແມ່ນຮູບກະຈົກຂອງອີກຂ້າງ ໜຶ່ງ. ຊື່ດັ່ງກ່າວໄດ້ມາຈາກ ຄຳ ນາມພາສາລາແຕັງຄລາສສິກ ສຳ ລັບຜ້າປູພື້ນຫລືຊ້ວນນ້ອຍ, ເຊິ່ງມັນໄດ້ຖືກຄິດວ່າຄ້າຍຄືກັນ.
ມຸມກະທູ້: ມຸມ ຂອງ ກະທູ້ ຂອງສະກູແມ່ນມຸມລວມຢູ່ລະຫວ່າງສາຍກະທູ້, ການວັດແທກໃນຍົນທີ່ປະກອບດ້ວຍແກນກະທູ້. ນີ້ແມ່ນປັດໃຈ ກຳ ນົດ ສຳ ລັບຮູບຊົງຂອງກະທູ້ສະກູ. ຄ່າມາດຕະຖານປະກອບມີ:
ຂໍ້ ຈຳ ກັດຂອງສະຖຽນລະພາບໃນທາງບວກ: ຂອບເຂດ ຈຳ ກັດຂອງສະຖຽນລະພາບໃນທາງບວກ (LPS) ຫຼື ມຸມສະຖຽນລະພາບທີ່ຂາດຫາຍໄປ (AVS) ແມ່ນມຸມທີ່ຕັ້ງຈາກແນວຕັ້ງທີ່ເຮືອຈະບໍ່ຢືນຢູ່ຕໍ່ໄປອີກແລ້ວແຕ່ຈະຫມູນວຽນ, ກາຍເປັນແນວທາງ, ຫລື ໝູນ ວຽນ.
ມຸມມອງຂອງມຸມມອງ: ມຸມຂອງມຸມມອງ ແມ່ນຕົວປ່ຽນທີ່ຕັດສິນ ສຳ ລັບຄວາມຮັບຮູ້ຂອງຂະ ໜາດ ຫລືການຄາດຄະເນຂອງຂະ ໜາດ ຂອງວັດຖຸໃດ ໜຶ່ງ.
Ben Lerner: Benjamin S. Lerner ແມ່ນນັກກະວີຊາວອາເມລິກາ, ນັກຂຽນ, ນັກຂຽນ, ແລະນັກວິຈານ. ລາວໄດ້ເປັນ Fulbright Scholar, ຜູ້ສຸດທ້າຍ ສຳ ລັບລາງວັນ Pulitzer for Fiction, ຜູ້ສຸດທ້າຍ ສຳ ລັບລາງວັນປື້ມແຫ່ງຊາດ, ຜູ້ສຸດທ້າຍ ສຳ ລັບລາງວັນ Book Book Critics Circle Award, Howard Foundation Fellow, Guggenheim Fellow, ແລະ MacArthur Fellow, ແລະອື່ນໆ ກຽດຕິຍົດ. ໃນປີ 2011 ລາວໄດ້ຮັບລາງວັນ "Preis der Stadt Münsterfür internesale Poesie", ຄົນອາເມລິກາຄົນ ທຳ ອິດທີ່ໄດ້ຮັບກຽດຕິຍົດ. Lerner ສອນຢູ່ວິທະຍາໄລ Brooklyn, ບ່ອນທີ່ທ່ານໄດ້ຖືກແຕ່ງຕັ້ງໃຫ້ເປັນອາຈານສອນພາສາອັງກິດທີ່ໂດດເດັ່ນໃນປີ 2016.
ມຸມເປົ້າ ໝາຍ: ມຸມມອງເປົ້າ ໝາຍ ແມ່ນຄວາມ ສຳ ຄັນຂອງສະຖານີການສັງເກດການຈາກຍານພາຫະນະທີ່ ກຳ ລັງສັງເກດ. ມັນອາດຈະຖືກ ນຳ ໃຊ້ເພື່ອ ຄຳ ນວນຈຸດປະສົງ ສຳ ລັບບັນຫາການຄວບຄຸມໄຟເມື່ອລະດັບຄວາມໄວຂອງລົດແລະຄວາມໄວສາມາດຄາດເດົາໄດ້ຈາກຂໍ້ມູນອື່ນໆ. ມຸມມອງເປົ້າ ໝາຍ ອາດຈະຖືກອະທິບາຍໄດ້ດີທີ່ສຸດຈາກຕົວຢ່າງຂອງເຮືອ ດຳ ນ້ ຳ ທີ່ ກຳ ລັງກະກຽມເປີດຕົວລູກສອນໄຟແບບກົງ (ບໍ່ແມ່ນຄົນຢູ່ເຮືອນ) ທີ່ເຮືອເປົ້າ ໝາຍ ເຄື່ອນຍ້າຍ. ເນື່ອງຈາກກະແສເດີນທາງເຄື່ອນທີ່ຂ້ອນຂ້າງຊ້າ, ຫລັກສູດ torpedo ຕ້ອງບໍ່ຕັ້ງເປົ້າ ໝາຍ, ແຕ່ໄປສູ່ຈຸດທີ່ຕັ້ງເປົ້າ ໝາຍ ເມື່ອ torpedo ໄປເຖິງມັນ. ມຸມມອງເປົ້າ ໝາຍ ແມ່ນໃຊ້ໃນການປະເມີນຫຼັກສູດເປົ້າ ໝາຍ.
ແຜ່ນມຸມ: ແຜ່ນມຸມ ແມ່ນອຸປະກອນເຮັດວຽກທີ່ໃຊ້ເປັນອຸປະກອນໃນການເຮັດໂລຫະ.
ໂຄມໄຟ Anglepoise: ໂຄມໄຟ Anglepoise ແມ່ນ ໂຄມໄຟ ແຂນທີ່ມີຄວາມສົມດຸນທີ່ຖືກອອກແບບໃນປີ 1932 ໂດຍນັກອອກແບບຊາວອັງກິດ George Carwardine.
ໄປສະນີ (ໂຄງສ້າງ): ກະ ທູ້ ແມ່ນການສະ ໜັບ ສະ ໜູນ ດ້ານແນວຕັ້ງຫຼືຫຼັກທີ່ຢູ່ໃນໂຄງສ້າງທີ່ຄ້າຍຄືກັບຖັນຫຼືເສົາ, ແຕ່ວ່າ ຄຳ ປະໂຫຍກໂດຍທົ່ວໄປ ໝາຍ ເຖິງໄມ້ແຕ່ອາດຈະເປັນໂລຫະຫຼືຫີນ. ສະຕູດິໂອໃນການກໍ່ສ້າງອາຄານໄມ້ຫລືໂລຫະແມ່ນຄ້າຍຄືກັນແຕ່ມີ ໜ້າ ທີ່ເບົາກວ່າການໄປສະນີແລະເສັ້ນດ່າງອາດຈະຄ້າຍຄືກັບ stud ຫຼືເຮັດເປັນເຊືອກຜູກ. ໃນປະເທດອັງກິດ, strut ອາດຈະຄ້າຍຄືກັນກັບໂພດແຕ່ບໍ່ແບກເສົາ. ໃນເສົາການກໍ່ສ້າງໄມ້ໂດຍປົກກະຕິແລ້ວແມ່ນລົງຈອດໃສ່ດິນຊາຍ, ແຕ່ວ່າໃນອາຄານທີ່ຫາຍາກປະເພດໄປສະນີອາດຈະສືບຕໍ່ໄປເຖິງພື້ນຖານທີ່ເອີ້ນວ່າບ່ອນຝັງດິນທີ່ຖືກລົບກວນຫຼືເຂົ້າໄປໃນພື້ນດິນທີ່ເອີ້ນວ່າແຜ່ນດິນໂລກ, ໜ້າ ດິນ, ຫຼືການກໍ່ສ້າງຫຼັງຈາກນັ້ນ. ໂພສຍັງເປັນສ່ວນປະກອບພື້ນຖານໃນຮົ້ວ. ຄຳ ສັບທີ່ວ່າ "jack" ແລະ "cripple" ແມ່ນໃຊ້ກັບ stud ແລະ short rafters ແຕ່ບໍ່ແມ່ນໂພດ, ຍົກເວັ້ນໃນ ຄຳ ສັບທີ່ພິເສດຂອງການຍ້າຍ.
ສາມຫລ່ຽມ: ສາມຫລ່ຽມ ແມ່ນ ຮູບສີ່ຫລ່ຽມ ທີ່ມີສາມຂອບແລະສາມດ້ານ. ມັນແມ່ນ ໜຶ່ງ ໃນບັນດາຮູບຮ່າງພື້ນຖານໃນເລຂາຄະນິດ. ສາມຫລ່ຽມທີ່ມີແນວຕັ້ງ A , B , ແລະ C ແມ່ນ ໝາຍ ເຖິງ .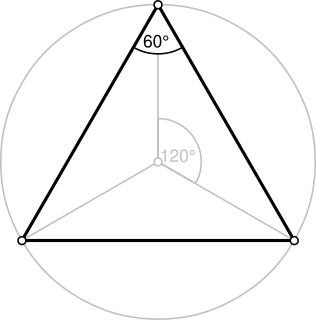
Guillemet: Guillemets ແມ່ນຄູ່ຂອງເຄື່ອງ ໝາຍ ວັກໃນຮູບແບບສອງຂ້າງຂອງ chevrons, « ແລະ » , ໃຊ້ເປັນເຄື່ອງ ໝາຍ ວົງຢືມໃນຫລາຍພາສາ. ໃນບາງສ່ວນຂອງພາສາເຫຼົ່ານີ້ "ດຽວ" Guillemet <ແລະ>, ໄດ້ຖືກນໍາໃຊ້ສໍາລັບວົງຢືມພາຍໃນວົງຢືມຄົນອື່ນໄດ້. Guillemets ບໍ່ໄດ້ຖືກ ນຳ ໃຊ້ໃນພາສາອັງກິດຢ່າງເປັນທາງການ.
ເຄື່ອງ ໝາຍ ວົງຢືມ: ເຄື່ອງ ໝາຍ ວົງຢືມ , ເຊິ່ງເອີ້ນກັນວ່າ ຄຳ ເວົ້າ , ເຄື່ອງ ໝາຍ ການອ້າງອີງ , ເຄື່ອງ ໝາຍ ການເວົ້າ , ເຄື່ອງ ໝາຍ , ຫຼື ເຄື່ອງ ໝາຍ ເວົ້າ ແມ່ນເຄື່ອງ ໝາຍ ວັກທີ່ໃຊ້ເປັນຄູ່ໃນລະບົບການຂຽນຕ່າງໆເພື່ອ ກຳ ນົດ ຄຳ ເວົ້າ, ຄຳ ເວົ້າ, ຫຼືປະໂຫຍກໂດຍກົງ. ຄູ່ນີ້ປະກອບດ້ວຍເຄື່ອງ ໝາຍ ເປີດວົງຢືມແລະເຄື່ອງ ໝາຍ ປິດວົງຢືມເຊິ່ງອາດຈະຫລືບໍ່ແມ່ນຕົວລະຄອນດຽວກັນ.
ການຕິດຕາມ: rafter ແມ່ນ ໜຶ່ງ ໃນບັນດາສະມາຊິກຂອງໂຄງສ້າງທີ່ມີຄ້ອຍໆເຊັ່ນ: ທ່ອນໄມ້ທີ່ຂະຫຍາຍຈາກສັນຕາມລວງຍາວຫຼືສະໂພກໄປຫາແຜ່ນຜະ ໜັງ, ຂອບທາງຂ້າງຫຼື eave, ແລະທີ່ຖືກອອກແບບມາເພື່ອສະ ໜັບ ສະ ໜູນ ແຜ່ນຮອງຫລັງຄາ, ຫລັງຄາແລະພາລະຂອງມັນທີ່ກ່ຽວຂ້ອງ. ຄູ່ຂອງ rafters ຖືກເອີ້ນວ່າ ຄູ່ຜົວເມຍ . ໃນການກໍ່ສ້າງເຮືອນ, rafters ແມ່ນເຮັດດ້ວຍໄມ້ປົກກະຕິ. rafters ທີ່ຖືກສະແດງອອກແມ່ນລັກສະນະຂອງຮູບແບບຫລັງຄາແບບດັ້ງເດີມ.
ພະຍາດຕາຕໍ້: ພະຍາດຕາຕໍ້ ແມ່ນກຸ່ມຂອງພະຍາດຕາເຊິ່ງສົ່ງຜົນໃຫ້ເກີດຄວາມເສຍຫາຍຕໍ່ເສັ້ນປະສາດຕາແລະເຮັດໃຫ້ສາຍຕາເສື່ອມ. ປະເພດທີ່ພົບເລື້ອຍທີ່ສຸດແມ່ນ ໂຣກຕາຕໍ້ , ໃນມຸມທີ່ລະບາຍນ້ ຳ ສຳ ລັບທາດແຫຼວພາຍໃນຕາຍັງເປີດຢູ່, ມີຊະນິດທີ່ພົບ ໜ້ອຍ ທີ່ສຸດລວມທັງພະ ຍາດຕາຕໍ້ຕຶບແລະເປັນຕາຕໍ້ ປົກກະຕິ. ພະຍາດຕາຕໍ້ເປີດຂື້ນພັດທະນາຊ້າໆຕາມເວລາແລະບໍ່ມີອາການເຈັບຫຍັງເລີຍ. ວິໄສທັດຕໍ່ພວງມະໄລອາດຈະເລີ່ມຫລຸດລົງ, ປະຕິບັດຕາມສາຍຕາກາງ, ເຮັດໃຫ້ຕາບອດຖ້າບໍ່ໄດ້ຮັບການປິ່ນປົວ. ພະຍາດຕາຕໍ້ທີ່ປິດແລ້ວສາມາດ ນຳ ສະ ເໜີ ຄ່ອຍໆຫລືກະທັນຫັນ. ການ ນຳ ສະ ເໜີ ຢ່າງກະທັນຫັນອາດຈະມີອາການເຈັບຕາຮຸນແຮງ, ມົວຕາ, ມຶນເມົາປານກາງ, ຕາແດງ, ແລະປວດຮາກ. ການສູນເສຍວິໄສທັດຈາກໂຣກຕາຕໍ້, ເມື່ອມັນເກີດຂຶ້ນ, ແມ່ນຖາວອນ. ຕາທີ່ໄດ້ຮັບຜົນກະທົບຈາກພະຍາດຕາຕໍ້ແມ່ນຖືກກ່າວເຖິງວ່າເປັນ ຕາຕໍ້ .
ການແກ້ໄຂບັນຫາການຖ່າຍຮູບແບບມຸມ: ການແກ້ໄຂບັນຫາດ້ານການຖ່າຍຮູບມຸມ ( ARPES ) ແມ່ນເຕັກນິກການທົດລອງທີ່ໃຊ້ໃນຟີຊິກທີ່ມີ ສານປົນເປື້ອນ ເພື່ອກວດສອບພະລັງງານທີ່ອະນຸຍາດແລະປັດຈຸບັນຂອງເອເລັກໂຕຣນິກໃນວັດສະດຸ, ໂດຍປົກກະຕິແລ້ວແມ່ນກ້ອນຫີນທີ່ແຂງແກ່ນ. ມັນແມ່ນອີງໃສ່ຜົນກະທົບຂອງ photoelectric, ເຊິ່ງໃນນັ້ນ photon ເຂົ້າມາຂອງພະລັງງານທີ່ພຽງພໍຈະປະຕິເສດເອເລັກໂຕຣນິກຈາກພື້ນທີ່ຂອງວັດສະດຸ. ໂດຍການວັດແທກໂດຍກົງກ່ຽວກັບພະລັງງານທາງດ້ານ kinetic ແລະການແຈກຢາຍມຸມຂອງເຄື່ອງຖ່າຍພາບທີ່ຖືກປ່ອຍອອກມາ, ເຕັກນິກສາມາດວາງແຜນໂຄງສ້າງຂອງແຖບເອເລັກໂຕຣນິກແລະພື້ນຜິວຂອງ Fermi. ARPES ແມ່ນ ເໝາະ ສົມທີ່ສຸດ ສຳ ລັບການສຶກສາເອກະສານ ໜຶ່ງ ຫຼືສອງມິຕິ. ມັນໄດ້ຖືກນໍາໃຊ້ໂດຍນັກຟິສິກສາດເພື່ອຄົ້ນຄວ້າພະລັງງານໄຟຟ້າທີ່ມີອຸນຫະພູມສູງ, graphene, ວັດສະດຸທາງດ້ານພູມສາດ, ລັດ quantum ດີ, ແລະວັດສະດຸທີ່ສະແດງຄື້ນຄວາມຖີ່ຂອງການຮັບຜິດຊອບ.
ເຄື່ອງບົດມຸມ: ເຄື່ອງຂັງມູມ , ເຊິ່ງເອີ້ນກັນວ່າເຄື່ອງບົດ ຂ້າງ ຫລື ແຜ່ນເຄື່ອງບົດ , ແມ່ນເຄື່ອງມືພະລັງງານທີ່ໃຊ້ດ້ວຍມືໃຊ້ ສຳ ລັບການປັ້ນແລະຂັດ. ເຖິງແມ່ນວ່າຖືກພັດທະນາໃນເບື້ອງຕົ້ນເປັນເຄື່ອງມື ສຳ ລັບແຜ່ນທີ່ຫຍໍ້ທີ່ແຂງກະດ້າງ, ການມີແຫຼ່ງພະລັງງານທີ່ປ່ຽນແປງໄດ້ກະຕຸ້ນໃຫ້ການ ນຳ ໃຊ້ຂອງມັນມີເຄື່ອງຕັດແລະເອກະສານຄັດຕິດຫຼາກຫຼາຍ.
ໂຮງຮຽນ Angle ຂອງ Orthodontia: ໂຮງຮຽນ Angle of Orthodontia ແມ່ນໂຮງຮຽນ ທຳ ອິດຂອງ orthodontics ໃນໂລກ, ສ້າງຕັ້ງຂື້ນໂດຍ Edward Angle ໃນປີ 1899. ໂຮງຮຽນໄດ້ສອນນັກຮຽນແຂ້ວຂອງຕົນໃນໄລຍະເວລາ 3-6 ອາທິດ. ໂຮງຮຽນໄດ້ຈົບການສຶກສາ 183 ນັກຮຽນຈົນກ່ວາມັນປິດໃນປີ 1927. ໃນບັນດານັກຮຽນທີ່ຈົບການສຶກສາ, ນັກສຶກສາ 25 ຄົນໄດ້ກາຍເປັນປະທານສະມາຄົມແພດ ໝໍ ແຂ້ວຂອງອາເມລິກາ, ນັກຮຽນ 11 ຄົນໄດ້ກາຍເປັນຫົວ ໜ້າ ພະແນກ Orthodontic ແລະນັກຮຽນ 3 ຄົນກາຍເປັນສາຂາບໍລິຫານແຂ້ວ.
ວາວ piston ບ່ອນນັ່ງມຸມ: ປ່ຽງ piston ບ່ອນນັ່ງມຸມ ແມ່ນ ປ່ຽງ ທີ່ຄວບຄຸມແບບປອດອັກເສບດ້ວຍຕົວປະຕິບັດ piston ທີ່ໃຫ້ການປະຕິບັດແບບເສັ້ນເພື່ອຍົກສາຍປະທັບຕາຈາກບ່ອນນັ່ງຂອງມັນ. ບ່ອນນັ່ງໄດ້ຖືກຕັ້ງຢູ່ໃນມຸມເພື່ອສະຫນອງການໄຫຼສູງສຸດທີ່ເປັນໄປໄດ້ໃນເວລາທີ່ unseated. ປ່ຽງ piston ບ່ອນນັ່ງມຸມແມ່ນເຫມາະສົມໂດຍສະເພາະກັບຄໍາຮ້ອງສະຫມັກທີ່ມີອຸນຫະພູມສູງແລະອັດຕາການໄຫຼທີ່ມີຄວາມຕ້ອງການສູງ, ເຊັ່ນ: ອາຍຫຼືນ້ໍາ. ໃນເວລາທີ່ ນຳ ໃຊ້ໃນການປີ້ນກັບກັນບາງຮູບແບບຂອງປ່ຽງ piston ບ່ອນນັ່ງມຸມຈະລົບລ້າງຄ້ອນນ້ໍາໃນເວລາທີ່ປະຕິບັດງານ.
ບ່ອນທີ່ມີຮົ່ມມຸມ: ບ່ອນທີ່ມີຮົ່ມມຸມ ແມ່ນມຸງຂອງຄອບຄົວ Noctuidae. ຊະນິດນີ້ຖືກອະທິບາຍໂດຍ Carl Linnaeus ຄັ້ງ ທຳ ອິດໃນ 1758 ຄັ້ງ ທີ 10 ຂອງ ລາວໃນລະບົບ Systema Naturae . ມັນໄດ້ຖືກແຈກຢາຍໄປທົ່ວເອີຣົບຈົນເຖິງພາກຕາເວັນອອກໄກຄືກັບ Urals ແລະໃນ Azores, ໃນ Algeria, ແລະໃນ Asia Minor, Armenia, ແລະ Syria. ມັນແມ່ນການເຄື່ອນຍ້າຍຢ່າງແຮງ.
ໂກງໃນໂປerກເກີ: ການໂກງໃນໂປpokກເກີ ແມ່ນການປະພຶດໃດໆນອກກົດລະບຽບທີ່ມີຈຸດປະສົງເພື່ອໃຫ້ປະໂຫຍດທີ່ບໍ່ຍຸດຕິ ທຳ ຕໍ່ຜູ້ຫຼີ້ນ ໜຶ່ງ ຫລືຫຼາຍຄົນ.
ສາຍແຫວນ: ໃນເຄມີສາດອິນຊີ, ສາຍແຫວນ ແມ່ນປະເພດຂອງຄວາມບໍ່ແນ່ນອນທີ່ມີຢູ່ໃນເວລາທີ່ພັນທະບັດໃນຮູບແບບໂມເລກຸນເປັນມຸມທີ່ຜິດປົກກະຕິ. ສາຍພັນແມ່ນໄດ້ຖືກປຶກສາຫາລືຫຼາຍທີ່ສຸດ ສຳ ລັບວົງແຫວນນ້ອຍໆເຊັ່ນ: ວົງວຽນແລະ cyclobutanes ເຊິ່ງມຸມພາຍໃນຂອງມັນມີຂະ ໜາດ ນ້ອຍກ່ວາມູນຄ່າທີ່ ເໝາະ ສົມປະມານ 109 °. ເນື່ອງຈາກຄວາມກົດດັນສູງຂອງພວກມັນ, ຄວາມຮ້ອນຂອງການເຜົາ ໄໝ້ ສຳ ​​ລັບແຫວນນ້ອຍໆເຫຼົ່ານີ້ແມ່ນສູງຂື້ນ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ຜົນລວມຂອງມຸມຂອງສາມຫຼ່ຽມ: ໃນພື້ນທີ່ Euclidean, ຜົນລວມຂອງມຸມຂອງສາມຫຼ່ຽມ ເທົ່າກັບມຸມກົງ .A ສາມຫລ່ຽມມີສາມມຸມ, ໜຶ່ງ ຢູ່ແຕ່ລະວົງແຫວນ, ຕິດກັບສອງຂ້າງຕິດກັນ.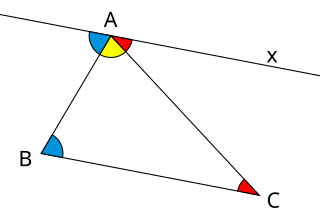
ມຸມພາຍໃນແລະພາຍນອກ: ໃນເລຂາຄະນິດ, ມຸມຂອງ polygon ແມ່ນຖືກສ້າງຕັ້ງຂື້ນໂດຍສອງດ້ານຂອງ polygon ທີ່ແບ່ງປັນຈຸດຈົບ. ສຳ ລັບຮູບສີ່ຫລ່ຽມທີ່ລຽບງ່າຍ (ບໍ່ກ່ຽວຂ້ອງກັບຕົວເອງ), ບໍ່ວ່າມັນຈະເປັນຮູບໂຄ້ງຫລືບໍ່ໂຄ້ງ, ມຸມນີ້ເອີ້ນວ່າ ມຸມ ພາຍໃນ ຖ້າວ່າຈຸດໃດ ໜຶ່ງ ພາຍໃນມຸມແມ່ນຢູ່ພາຍໃນຂອງ polygon. ຮູບສາມຫລ່ຽມມີມຸມ ໜຶ່ງ ພາຍໃນຢ່າງຕໍ່ເນື່ອງ.
ມຸມພາຍໃນແລະພາຍນອກ: ໃນເລຂາຄະນິດ, ມຸມຂອງ polygon ແມ່ນຖືກສ້າງຕັ້ງຂື້ນໂດຍສອງດ້ານຂອງ polygon ທີ່ແບ່ງປັນຈຸດຈົບ. ສຳ ລັບຮູບສີ່ຫລ່ຽມທີ່ລຽບງ່າຍ (ບໍ່ກ່ຽວຂ້ອງກັບຕົວເອງ), ບໍ່ວ່າມັນຈະເປັນຮູບໂຄ້ງຫລືບໍ່ໂຄ້ງ, ມຸມນີ້ເອີ້ນວ່າ ມຸມ ພາຍໃນ ຖ້າວ່າຈຸດໃດ ໜຶ່ງ ພາຍໃນມຸມແມ່ນຢູ່ພາຍໃນຂອງ polygon. ຮູບສາມຫລ່ຽມມີມຸມ ໜຶ່ງ ພາຍໃນຢ່າງຕໍ່ເນື່ອງ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
ຜົນລວມຂອງມຸມຂອງສາມຫຼ່ຽມ: ໃນພື້ນທີ່ Euclidean, ຜົນລວມຂອງມຸມຂອງສາມຫຼ່ຽມ ເທົ່າກັບມຸມກົງ .A ສາມຫລ່ຽມມີສາມມຸມ, ໜຶ່ງ ຢູ່ແຕ່ລະວົງແຫວນ, ຕິດກັບສອງຂ້າງຕິດກັນ.
ບັນຊີລາຍຊື່ຂອງຕົວຕົນ trigonometric: ໃນຄະນິດສາດ, ຕົວຕົນຂອງ trigonometric ແມ່ນຄວາມເທົ່າທຽມກັນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ຂອງ trigonometric ແລະເປັນຄວາມຈິງ ສຳ ລັບທຸກໆຄຸນຄ່າຂອງຕົວແປທີ່ເກີດຂື້ນເຊິ່ງທັງສອງດ້ານຂອງຄວາມເທົ່າທຽມກັນໄດ້ຖືກ ກຳ ນົດ. ເລຂາຄະນິດ, ເຫຼົ່ານີ້ແມ່ນຕົວຕົນທີ່ກ່ຽວຂ້ອງກັບ ໜ້າ ທີ່ບາງຢ່າງຂອງ ໜຶ່ງ ຫຼືຫຼາຍມຸມ. ພວກມັນແຕກຕ່າງຈາກເອກະລັກຂອງສາມຫຼ່ຽມ, ເຊິ່ງແມ່ນຕົວຕົນທີ່ມີຄວາມກ່ຽວຂ້ອງກັບມຸມແຕ່ມັນກໍ່ກ່ຽວຂ້ອງກັບຄວາມຍາວຂ້າງຫຼືລວງຍາວອື່ນໆຂອງສາມຫຼ່ຽມ.
Angle Tarn (Langstrath): Angle Tarn ແມ່ນເສັ້ນດ້າຍທີ່ຢູ່ທາງ ເໜືອ ຂອງ Bowfell ໃນເມືອງ Lake English. ມັນດູດເຂົ້າ Langstrath Beck.
ມຸມ: The Angles ແມ່ນ ໜຶ່ງ ໃນປະຊາຊົນຊາວເຢຍລະມັນຕົ້ນຕໍທີ່ໄດ້ຕັ້ງຖິ່ນຖານຢູ່ປະເທດອັງກິດໃນສະ ໄໝ ຫລັງ Roman. ພວກເຂົາໄດ້ສ້າງຕັ້ງຫລາຍອານາຈັກຂອງ Heptarchy ໃນອັງກິດອັງກິດ, ແລະຊື່ຂອງພວກມັນແມ່ນຮາກຂອງຊື່ ອັງກິດ . ອີງຕາມການ Tacitus, ການຂຽນກ່ອນທີ່ພວກເຂົາຈະຍ້າຍໄປປະເທດອັງກິດ, Angles ໄດ້ອາໄສຢູ່ຄຽງຄູ່ກັບ Langobards ແລະ Semnones ໃນເຂດປະຫວັດສາດ Schleswig ແລະ Holstein, ເຊິ່ງປະຈຸບັນນີ້ແມ່ນພາກສ່ວນ ໜຶ່ງ ຂອງພາກໃຕ້ເດນມາກແລະພາກ ເໜືອ ຂອງເຢຍລະມັນ (Schleswig-Holstein).
ການກວດຫາມຸມ: Trisection ມຸມ ແມ່ນບັນຫາແບບຄລາສສິກຂອງເຂັມທິດແລະການສ້າງກົງຂອງຄະນິດສາດບູຮານ. ມັນກ່ຽວຂ້ອງກັບການສ້າງມຸມເທົ່າກັບ ໜຶ່ງ ສ່ວນສາມຂອງມຸມທີ່ຕົນເອງມັກ, ໂດຍໃຊ້ສອງເຄື່ອງມືເທົ່ານັ້ນ: ເສັ້ນກົງທີ່ບໍ່ມີເຄື່ອງ ໝາຍ ແລະເຂັມທິດ.
ການກວດຫາມຸມ: Trisection ມຸມ ແມ່ນບັນຫາແບບຄລາສສິກຂອງເຂັມທິດແລະການສ້າງກົງຂອງຄະນິດສາດບູຮານ. ມັນກ່ຽວຂ້ອງກັບການສ້າງມຸມເທົ່າກັບ ໜຶ່ງ ສ່ວນສາມຂອງມຸມທີ່ຕົນເອງມັກ, ໂດຍໃຊ້ສອງເຄື່ອງມືເທົ່ານັ້ນ: ເສັ້ນກົງທີ່ບໍ່ມີເຄື່ອງ ໝາຍ ແລະເຂັມທິດ.
Chloropteryx tepperaria: Chloropteryx tepperaria , ເມັນ emerald ທີ່ມີປີກມຸມ, ແມ່ນແມງກະ ເບື້ອ ຂອງຄອບຄົວ Geometridae. ຊະນິດນີ້ຖືກອະທິບາຍເປັນຄັ້ງ ທຳ ອິດໂດຍ George Duryea Hulst ໃນປີ 1886 ແລະມັນໄດ້ຖືກພົບເຫັນຢູ່ໃນພາກຕາເວັນອອກສຽງໃຕ້ຂອງສະຫະລັດ.
Chloropteryx tepperaria: Chloropteryx tepperaria , ເມັນ emerald ທີ່ມີປີກມຸມ, ແມ່ນແມງກະ ເບື້ອ ຂອງຄອບຄົວ Geometridae. ຊະນິດນີ້ຖືກອະທິບາຍເປັນຄັ້ງ ທຳ ອິດໂດຍ George Duryea Hulst ໃນປີ 1886 ແລະມັນໄດ້ຖືກພົບເຫັນຢູ່ໃນພາກຕາເວັນອອກສຽງໃຕ້ຂອງສະຫະລັດ.
Chloropteryx tepperaria: Chloropteryx tepperaria , ເມັນ emerald ທີ່ມີປີກມຸມ, ແມ່ນແມງກະ ເບື້ອ ຂອງຄອບຄົວ Geometridae. ຊະນິດນີ້ຖືກອະທິບາຍເປັນຄັ້ງ ທຳ ອິດໂດຍ George Duryea Hulst ໃນປີ 1886 ແລະມັນໄດ້ຖືກພົບເຫັນຢູ່ໃນພາກຕາເວັນອອກສຽງໃຕ້ຂອງສະຫະລັດ.
Chloropteryx tepperaria: Chloropteryx tepperaria , ເມັນ emerald ທີ່ມີປີກມຸມ, ແມ່ນແມງກະ ເບື້ອ ຂອງຄອບຄົວ Geometridae. ຊະນິດນີ້ຖືກອະທິບາຍເປັນຄັ້ງ ທຳ ອິດໂດຍ George Duryea Hulst ໃນປີ 1886 ແລະມັນໄດ້ຖືກພົບເຫັນຢູ່ໃນພາກຕາເວັນອອກສຽງໃຕ້ຂອງສະຫະລັດ.
Angleball: Angleball ແມ່ນອົງກອນອອກ ກຳ ລັງກາຍກິລາທີ່ຈົດທະບຽນແລະເປັນຜູ້ຜະລິດອຸປະກອນທີ່ມີສິດທິບັດ ສຳ ລັບກິລາເກົ່າແກ່ທີ່ສຸດຂອງອາເມລິກາ ເໜືອ, anejodi ກົດລະບຽບຂອງ Anejodi ຂອງ Angleball ໄດ້ຖືກຈັດຕັ້ງຂື້ນ ໃໝ່ ຕາມປະເພນີຂອງຊາວອາເມລິກາໃນໄລຍະສົງຄາມໂລກຄັ້ງທີ 2 ທີ່ມະຫາວິທະຍາໄລ Brown ໂດຍວິທະຍາໄລ Hall of Fame ແລະຄູຝຶກບານບ້ວງ Charles " Rip" Engle ເພື່ອຮັກສາການບໍລິການຂອງສົງຄາມໂລກຄັ້ງທີ 2 ຂອງອາເມລິກາໃຫ້ ເໝາະ ສົມກ່ອນການປະຕິບັດງານ. ອຸປະກອນ Angleball ປະຈຸບັນມີຄົນຫຼີ້ນ 1,000,000+ ຄົນໃນສະຫະລັດແລະໃນທົ່ວໂລກແລະເພື່ອຄວາມເຢັນໃນ NFL ແລະໂດຍທີມນັກກິລາໂອລິມປິກທີມ USA. ນັບຕັ້ງແຕ່ປີ 2014, Angleball ໄດ້ສ້າງແຮງບັນດານໃຈໃຫ້ກັບເກມປະເພດເກມທີ່ຂາຍດີທີ່ສຸດໃນໂລກ, Call of Duty, ທີ່ເອີ້ນວ່າ Uplink. International Angleball ມີ 13 ປະເທດສະມາຊິກໃນປະຈຸບັນ. ອົງການ Angleball ໃຫ້ກຽດແກ່ມໍລະດົກວັດຖຸບູຮານຂອງຕົນໂດຍການຊຸກຍູ້ໃຫ້ກຸ່ມຜະລິດອຸປະກອນ anejodi ຂອງຕົນເອງເຂົ້າໃນການວັດແທກທີ່ມີສິດທິບັດຂອງ Angleball, ໂດຍ ນຳ ໃຊ້ວັດຖຸດິບທີ່ມີຢູ່ຫຼື ທຳ ມະຊາດ, ຕາບໃດທີ່ອຸປະກອນດັ່ງກ່າວບໍ່ໄດ້ຂາຍ. Angleball ແມ່ນເຄື່ອງ ໝາຍ ການຄ້າທີ່ຈົດທະບຽນແລະຖືກຂາຍໂດຍສະເພາະບໍລິສັດ Angleball.
Jean-Henri d'Anglebert: Jean-Henri d'Anglebert ແມ່ນນັກຂຽນພາສາຝຣັ່ງ, ນັກສະແດງ harpsichordist ແລະອົງການຈັດຕັ້ງ. ລາວແມ່ນ ໜຶ່ງ ໃນບັນດານັກແຕ່ງເພງທີ່ ສຳ ຄັນທີ່ສຸດໃນສະ ໄໝ ຂອງລາວ.
Anglecot: The Anglecot , ເຊິ່ງເອີ້ນວ່າ Potter Residence , ແມ່ນບ່ອນຢູ່ອາໄສທາງປະຫວັດສາດໃນເຂດ Chestnut Hill ໃນເມືອງ Philadelphia, Pennsylvania, ສະຫະລັດອາເມລິກາ. ມັນຖືກອອກແບບໂດຍສະຖາປະນິກ Philadelphia ທີ່ສັງເກດເຫັນ Wilson Eyre ສຳ ລັບ Charles Adams Potter (1860-1925), ຜູ້ຜະລິດ linoleum.
ເພງ Ariadne: Ariadne ariadne , ເຄື່ອງປະດັບເປັນ ລ່ຽມ , ແມ່ນຊະນິດຂອງ butterfly nymphalid ພົບເຫັນຢູ່ໃນອາຊີ.
Allotinus fabius: Allotinus fabius , the darkie angled , ແມ່ນຜີເສື້ອຜີເສື້ອນ້ອຍທີ່ພົບເຫັນໃນປະເທດອິນເດຍ, ມຽນມາແລະອາຊີຕາເວັນອອກສ່ຽງໃຕ້ເຊິ່ງເປັນຂອງ lycaenids ຫຼື blues ຄອບຄົວ.
sabulifera Anomis: Anomis sabulifera , ແກ້ວປະເສີດທີ່ມີມຸມ ຫລື jute ເຄິ່ງຮອບ ແອວ , ແມ່ນມຸງ ຂອງຄອບຄົວ Erebidae. ຊະນິດດັ່ງກ່າວຖືກອະທິບາຍເປັນຄັ້ງ ທຳ ອິດໂດຍ Achille Guenéeໃນປີ 1852. ມັນມີການກະຈາຍພັນ Paleot ເຂດຮ້ອນແລະຕັ້ງແຕ່ອາຟຣິກາຕາເວັນອອກຫາອິນເດຍ, ສີລັງກາແລະອົດສະຕາລີ. ບັນທຶກດຽວໄດ້ຖືກພົບເຫັນຈາກອັງກິດ.
Ancylolomia chrysographellus: Ancylolomia chrysographellus , ແມ່ພະຍາດ ຫຍ້າທີ່ເປັນມຸມ , ແມ່ນຊະນິດຂອງແມງກະເບື້ອໃນຄອບຄົວ Crambidae. ມັນພົບຢູ່ Cyprus ແລະໃນ Kenya, Uganda, Yemen, India, Pakistan, Sri Lanka, ມຽນມາ, ຈີນ, ເກົາຫຼີ, ຍີ່ປຸ່ນ, ໄຕ້ຫວັນ, ຟີລິບປິນແລະອິນໂດເນເຊຍ.
Eurema desjardinsii: Eurema desjardinsii , ຫຍ້າສີເຫລືອງ , ເປັນຜີເສື້ອຂອງຄອບຄົວ Pieridae, ພົບຢູ່ໃນອາຟຣິກກາ.
Luffa acutangula: Luffa acutangula ແມ່ນປູກເປັນສິນຄ້າ ສຳ ລັບ ໝາກ ໄມ້ທີ່ບໍ່ມີ ກິ່ນຫອມ ເປັນຜັກ. ໝາກ ໄມ້ທີ່ແກ່ແມ່ນຖືກໃຊ້ເປັນຟອງນໍ້າ ທຳ ຄວາມສະອາດ. ໝາກ ຂອງມັນຄ້າຍຄືກັນກັບ ໝາກ ແຕງຫລື ໝາກ ແຄ້ງທີ່ມີສັນຕາມລວງຍາວ. ມັນຕັ້ງແຕ່ອາຊີກາງແລະພາກຕາເວັນອອກເຖິງອາຊີຕາເວັນອອກສ່ຽງໃຕ້. ມັນຍັງຖືກປູກເປັນຕົ້ນໄມ້ໃນສະຖານທີ່ທີ່ມີອາກາດທີ່ ໜາວ ເຢັນ. ຊື່ສາມັນອັງກິດປະກອບມີ Luffa ເປັນລ່ຽມ, ມະເຂືອມອນຈີນ, ນ້ໍາເຕົ້າຜ້າອາຫານ, ນ້ໍາເຕົ້າສັນຕາມລວງຍາວ, ຟອງນ້ໍານ້ໍາເຕົ້າ, ນ້ໍາເຕົ້າຜັກ, strainer ເຄືອ, ribbed ຮັງບວບ, ນ້ໍາເຕົ້າລຽບຄືເສັ້ນໄຫມ, ນ້ໍາເຕົ້າສັນຕາມລວງຍາວ, ຜ້າໄຫມນ້ໍາເຕົ້າ, ແລະ sinkwa towelsponge.
Caleta caleta: Caleta caleta , ຮູບສີ່ ຫລ່ຽມທີ່ ເປັນຮູບສີ່ ຫລ່ຽມ , ເປັນຊະນິດຂອງຜີເສື້ອສີຟ້າທີ່ພົບໃນ Sulawesi.
ຫິນອ່ອນ Lythrum alatum, ເປັນທີ່ຮູ້ຈັກທົ່ວໄປເປັນ loosestrife ໄຂບໍ່ໄດ້, lythrum ມີປີກຫຼືເປັນລ່ຽມສີມ່ວງ, loosestrife, ເປັນຊະນິດຂອງການອອກດອກພືດທີ່ເປັນຂອງຄອບຄົວ Lythraceae ໄດ້. ມັນແຜ່ຂະຫຍາຍໄປທົ່ວເຂດດິນທາມໃນພາກກາງແລະພາກຕາເວັນອອກຂອງສະຫະລັດແລະ Ontario.
Anteos maerula: Anteos maerula , ຊູນຟູຣິກ ຫລື ມຸມຊູນຟູຣິກ , ສີສົ້ມ , ແມ່ນຜີເສື້ອຂອງຄອບຄົວ Pieridae. ມັນໄດ້ຖືກພົບເຫັນຈາກປະເທດເປຣູກັບເມັກຊິໂກ. ເປັນສິ່ງທີ່ຫາຍາກ, ຜູ້ອົບພະຍົບສາມາດພົບເຫັນຢູ່ທາງທິດຕາເວັນອອກຂອງ Nebraska, ທິດຕາເວັນອອກສຽງໃຕ້ Arizona, ທິດຕາເວັນຕົກສຽງໃຕ້ຂອງ New Mexico, ພາກໃຕ້ຂອງ Texas, ລັດ Mississippi ແລະ Florida.
Curetis acuta: Curetis acuta , ແສງຕາເວັນທີ່ ມີມຸມ ເປັນປະເພດຂອງ butterfly ແມ່ນຂອງຄອບຄົວ lycaenid. ມັນໄດ້ຖືກພົບເຫັນຢູ່ໃນພົບພູມ Indomalayan. Curetis acuta ແມ່ນສີມ້ວງທາງເພດເນື່ອງຈາກມີສີສັນທີ່ແຕກຕ່າງກັນຂອງປີກລະຫວ່າງເພດ, ແຕ່ວ່າປີກຂອງມັນທີ່ຄ້າຍຄືກັນແລະສີເງິນທີ່ສະທ້ອນແສງແດດ. ການສະທ້ອນແສງສະຫວ່າງໂດຍປີກດອກໄມ້ເງິນມີບົດບາດໃນການສັນຍານໃນລະຫວ່າງການບິນ, ການປຸ່ງແຕ່ງໃນເວລາທີ່ພັກຜ່ອນຫຼືໃນຊ່ວງເວລາ hibernation, ແລະອຸນຫະພູມໃນຮ່າງກາຍຫຼຸດລົງໂດຍການສະທ້ອນແສງແດດ
ເສືອໂຄ້ງ: ເສືອທີ່ ມີຮູບສີ່ຫລ່ຽມແມ່ນສາຍພັນຂອງຜີເສື້ອຜີວ ໜັງ Nymphalid ທີ່ຢູ່ໃນແດນ Danainae ມັນພົບຢູ່ Papua New Guinea ແລະເກາະ Solomon.
ຖານຂໍ້ມູນ: ພື້ນຖານ ຫລື ເສົາໄຟຟ້າ ແມ່ນໂຄງປະກອບພາຍນອກຈາກ ກຳ ແພງມ່ານຂອງປ້ອມປ້ອງກັນ, ສ່ວນຫຼາຍເປັນລ່ຽມເປັນຮູບຊົງແລະຕັ້ງຢູ່ແຈຂອງປ້ອມ. ພື້ນຖານທີ່ພັດທະນາຢ່າງເຕັມສ່ວນປະກອບດ້ວຍສອງ ໜ້າ ແລະສອງດ້ານ, ໂດຍໄຟຈາກບໍລິເວນທີ່ສາມາດປົກປ້ອງ ກຳ ແພງມ່ານແລະພື້ນທີ່ໃກ້ຄຽງ. ເມື່ອທຽບໃສ່ກັບບັນດາ ກຳ ລັງປ້ອງກັນປະເທດໃນຍຸກກາງທີ່ເຂົາເຈົ້າທົດແທນ, ກຳ ລັງປ້ອງກັນທີ່ຮອງຮັບໄດ້ສະ ເໜີ ໃຫ້ມີການຕໍ່ຕ້ານຕົວຕັ້ງຕົວຕີແລະຂອບເຂດທີ່ສູງກວ່າ ສຳ ລັບການປ້ອງກັນທີ່ມີຢູ່ໃນອາຍຸຂອງປືນໃຫຍ່ປືນໃຫຍ່. ໃນຖານະເປັນສະຖາປັດຕະຍະ ກຳ ການທະຫານ, ຖານທີ່ ໝັ້ນ ແມ່ນອົງປະກອບ ໜຶ່ງ ໃນແບບຂອງການເສີມສ້າງທີ່ໂດດເດັ່ນຈາກກາງສະຕະວັດທີ 16 ຫາກາງສະຕະວັດທີ 19.
ຖານຂໍ້ມູນ: ພື້ນຖານ ຫລື ເສົາໄຟຟ້າ ແມ່ນໂຄງປະກອບພາຍນອກຈາກ ກຳ ແພງມ່ານຂອງປ້ອມປ້ອງກັນ, ສ່ວນຫຼາຍເປັນລ່ຽມເປັນຮູບຊົງແລະຕັ້ງຢູ່ແຈຂອງປ້ອມ. ພື້ນຖານທີ່ພັດທະນາຢ່າງເຕັມສ່ວນປະກອບດ້ວຍສອງ ໜ້າ ແລະສອງດ້ານ, ໂດຍໄຟຈາກບໍລິເວນທີ່ສາມາດປົກປ້ອງ ກຳ ແພງມ່ານແລະພື້ນທີ່ໃກ້ຄຽງ. ເມື່ອທຽບໃສ່ກັບບັນດາ ກຳ ລັງປ້ອງກັນປະເທດໃນຍຸກກາງທີ່ເຂົາເຈົ້າທົດແທນ, ກຳ ລັງປ້ອງກັນທີ່ຮອງຮັບໄດ້ສະ ເໜີ ໃຫ້ມີການຕໍ່ຕ້ານຕົວຕັ້ງຕົວຕີແລະຂອບເຂດທີ່ສູງກວ່າ ສຳ ລັບການປ້ອງກັນທີ່ມີຢູ່ໃນອາຍຸຂອງປືນໃຫຍ່ປືນໃຫຍ່. ໃນຖານະເປັນສະຖາປັດຕະຍະ ກຳ ການທະຫານ, ຖານທີ່ ໝັ້ນ ແມ່ນອົງປະກອບ ໜຶ່ງ ໃນແບບຂອງການເສີມສ້າງທີ່ໂດດເດັ່ນຈາກກາງສະຕະວັດທີ 16 ຫາກາງສະຕະວັດທີ 19.
ວົງເລັບ: ວົງເລັບ ແມ່ນເຄື່ອງ ໝາຍ ວັກສອງອັນທີ່ມີຄວາມສູງທາງ ໜ້າ ຫລືດ້ານຫລັງທີ່ໃຊ້ທົ່ວໄປເພື່ອແຍກສ່ວນຂອງຂໍ້ຄວາມຫລືຂໍ້ມູນຈາກສິ່ງອ້ອມຂ້າງ. ການ ນຳ ໃຊ້ແບບປົກກະຕິໃນຄູ່ທີ່ມີຄວາມສອດຄ່ອງ, ວົງເລັບສ່ວນບຸກຄົນອາດຈະຖືກລະບຸວ່າເປັນວົງເລັບ ເບື້ອງຊ້າຍ ຫລື ຂວາ ຫຼືທາງເລືອກ, ວົງເລັບເປີດ ຫຼື ປິດວົງເລັບປິດ , ຕາມ ລຳ ດັບ, ຂື້ນກັບທິດທາງຂອງສະພາບການ.
ເພງ Ariadne: Ariadne ariadne , ເຄື່ອງປະດັບເປັນ ລ່ຽມ , ແມ່ນຊະນິດຂອງ butterfly nymphalid ພົບເຫັນຢູ່ໃນອາຊີ.
Allotinus fabius: Allotinus fabius , the darkie angled , ແມ່ນຜີເສື້ອຜີເສື້ອນ້ອຍທີ່ພົບເຫັນໃນປະເທດອິນເດຍ, ມຽນມາແລະອາຊີຕາເວັນອອກສ່ຽງໃຕ້ເຊິ່ງເປັນຂອງ lycaenids ຫຼື blues ຄອບຄົວ.
ສຽງຂອງຖ້ຽວບິນ: ພື້ນທີ່ ບິນ ຂອງ ກຳ ປັ່ນບັນທຸກເຮືອບິນແມ່ນ ໜ້າ ດິນທີ່ເຮືອບິນຂອງມັນບິນຂຶ້ນແລະລົງຈອດ, ທີ່ ສຳ ຄັນແມ່ນສະ ໜາມ ບິນນ້ອຍໆຢູ່ກາງທະເລ. ຢູ່ເທິງເຮືອນ້ອຍໆທີ່ບໍ່ມີການບິນເປັນພາລະກິດຕົ້ນຕໍ, ພື້ນທີ່ລົງຈອດ ສຳ ລັບເຮລິຄອບເຕີແລະເຮືອບິນ VTOL ອື່ນໆກໍ່ ໝາຍ ເຖິງຖ້ຽວບິນ. ໄລຍະທາງການຂອງກອງທັບເຮືອສະຫະລັດອາເມລິກາ ສຳ ລັບເຮືອເຫຼົ່ານີ້ແມ່ນ "ເຮືອທີ່ມີຄວາມສາມາດທາງອາກາດ".
ຮູບແບບ Usta: Usta angulata , ຈັກກະວານທີ່ມີມຸມ , ແມ່ນຊະນິດຂອງແມງກະເບື້ອໃນຄອບຄົວ Saturniidae ມັນຖືກພົບເຫັນຢູ່ໃນ Kenya, Tanzania, Somalia ແລະ Botswana.
ສຽງຂອງຖ້ຽວບິນ: ພື້ນທີ່ ບິນ ຂອງ ກຳ ປັ່ນບັນທຸກເຮືອບິນແມ່ນ ໜ້າ ດິນທີ່ເຮືອບິນຂອງມັນບິນຂຶ້ນແລະລົງຈອດ, ທີ່ ສຳ ຄັນແມ່ນສະ ໜາມ ບິນນ້ອຍໆຢູ່ກາງທະເລ. ຢູ່ເທິງເຮືອນ້ອຍໆທີ່ບໍ່ມີການບິນເປັນພາລະກິດຕົ້ນຕໍ, ພື້ນທີ່ລົງຈອດ ສຳ ລັບເຮລິຄອບເຕີແລະເຮືອບິນ VTOL ອື່ນໆກໍ່ ໝາຍ ເຖິງຖ້ຽວບິນ. ໄລຍະທາງການຂອງກອງທັບເຮືອສະຫະລັດອາເມລິກາ ສຳ ລັບເຮືອເຫຼົ່ານີ້ແມ່ນ "ເຮືອທີ່ມີຄວາມສາມາດທາງອາກາດ".
ແນ່ນອນດ້ານຕໍ່: A ແນ່ນອນດ້ານຫນ້າຕັ້ງຫຼື foregrip ເປັນແນ່ນອນດ້ານ pistol ຕັ້ງຕິດຕັ້ງຢູ່ທີ່ໂພດໃນຕອນທ້າຍຂອງ firearm ຍາວ, ບາເລນ, ອອກແບບມາສໍາລັບການໂລພໂດຍມືສະຫນັບສະຫນູນຫນ້າຜາກ.
angularis Cyrtodactylus: Cyrtodactylus angularis, ຍັງເປັນທີ່ຮູ້ຈັກທົ່ວໄປເປັນ gecko bow ນິ້ວມຸມຫຼື gecko ປ່າລ່ຽມ, ເປັນຊະນິດຂອງແລນໃນຄອບຄົວ Gekkonidae ໄດ້. ຊະນິດນີ້ແມ່ນແຜ່ລາມໄປສູ່ປະເທດໄທ.
sabulifera Anomis: Anomis sabulifera , ແກ້ວປະເສີດທີ່ມີມຸມ ຫລື jute ເຄິ່ງຮອບ ແອວ , ແມ່ນມຸງ ຂອງຄອບຄົວ Erebidae. ຊະນິດດັ່ງກ່າວຖືກອະທິບາຍເປັນຄັ້ງ ທຳ ອິດໂດຍ Achille Guenéeໃນປີ 1852. ມັນມີການກະຈາຍພັນ Paleot ເຂດຮ້ອນແລະຕັ້ງແຕ່ອາຟຣິກາຕາເວັນອອກຫາອິນເດຍ, ສີລັງກາແລະອົດສະຕາລີ. ບັນທຶກດຽວໄດ້ຖືກພົບເຫັນຈາກອັງກິດ.
Ancylolomia chrysographellus: Ancylolomia chrysographellus , ແມ່ພະຍາດ ຫຍ້າທີ່ເປັນມຸມ , ແມ່ນຊະນິດຂອງແມງກະເບື້ອໃນຄອບຄົວ Crambidae. ມັນພົບຢູ່ Cyprus ແລະໃນ Kenya, Uganda, Yemen, India, Pakistan, Sri Lanka, ມຽນມາ, ຈີນ, ເກົາຫຼີ, ຍີ່ປຸ່ນ, ໄຕ້ຫວັນ, ຟີລິບປິນແລະອິນໂດເນເຊຍ.
Eurema desjardinsii: Eurema desjardinsii , ຫຍ້າສີເຫລືອງ , ເປັນຜີເສື້ອຂອງຄອບຄົວ Pieridae, ພົບຢູ່ໃນອາຟຣິກກາ.
Lobelia anceps: Lobelia anceps , ທີ່ຮູ້ກັນທົ່ວໄປເປັນ lobelia ມຸມ , ແມ່ນພືດທີ່ເປັນປະເພດຫຍ້າຂະ ໜາດ ນ້ອຍໃນຄອບຄົວ Campanulaceae ທີ່ມີ ຖິ່ນ ກຳ ເນີດມາຈາກອົດສະຕາລີຕາເວັນຕົກ, ນິວຊີແລນ, ອາເມລິກາໃຕ້ແລະອາຟຣິກາໃຕ້.
Luffa acutangula: Luffa acutangula ແມ່ນປູກເປັນສິນຄ້າ ສຳ ລັບ ໝາກ ໄມ້ທີ່ບໍ່ມີ ກິ່ນຫອມ ເປັນຜັກ. ໝາກ ໄມ້ທີ່ແກ່ແມ່ນຖືກໃຊ້ເປັນຟອງນໍ້າ ທຳ ຄວາມສະອາດ. ໝາກ ຂອງມັນຄ້າຍຄືກັນກັບ ໝາກ ແຕງຫລື ໝາກ ແຄ້ງທີ່ມີສັນຕາມລວງຍາວ. ມັນຕັ້ງແຕ່ອາຊີກາງແລະພາກຕາເວັນອອກເຖິງອາຊີຕາເວັນອອກສ່ຽງໃຕ້. ມັນຍັງຖືກປູກເປັນຕົ້ນໄມ້ໃນສະຖານທີ່ທີ່ມີອາກາດທີ່ ໜາວ ເຢັນ. ຊື່ສາມັນອັງກິດປະກອບມີ Luffa ເປັນລ່ຽມ, ມະເຂືອມອນຈີນ, ນ້ໍາເຕົ້າຜ້າອາຫານ, ນ້ໍາເຕົ້າສັນຕາມລວງຍາວ, ຟອງນ້ໍານ້ໍາເຕົ້າ, ນ້ໍາເຕົ້າຜັກ, strainer ເຄືອ, ribbed ຮັງບວບ, ນ້ໍາເຕົ້າລຽບຄືເສັ້ນໄຫມ, ນ້ໍາເຕົ້າສັນຕາມລວງຍາວ, ຜ້າໄຫມນ້ໍາເຕົ້າ, ແລະ sinkwa towelsponge.
angaria Metarranthis: Angarranthis angularia , moth ທີ່ ມີຮູບຊົງເປັນ ລ່ຽມ , ແມ່ນຊະນິດຂອງແມງກະ ເບື້ອໃນຕະກູນ Geometridae. ມັນໄດ້ຖືກອະທິບາຍຄັ້ງ ທຳ ອິດໂດຍ William Barnes ແລະ James Halliday McDunnough ໃນປີ 1917 ແລະມັນຖືກພົບເຫັນຢູ່ໃນອາເມລິກາ ເໜືອ.
Paludella squarrosa: Paludella squarrosa ແມ່ນຊະນິດ moss ທີ່ເປັນຂອງຄອບຄົວ Meesiaceae.
Lathyrus angulatus: Lathyrus angulatus ແມ່ນຖົ່ວຖົ່ວຊະນິດ ໜຶ່ງ ທີ່ຮູ້ກັນໂດຍຊື່ສາມັນຕົ້ນ ຖົ່ວ .
Neptis quintilla: Neptis quintilla , ຮູບເງົາທີ່ມີຮູບຊົງ ນ້ອຍໆ , ແມ່ນຜີເສື້ອໃນຄອບຄົວ Nymphalidae. ມັນຖືກພົບເຫັນຢູ່ໃນ Guinea-Bissau, Guinea, Sierra Leone, Ivory Coast, Ghana, Nigeria, Cameroon, Angola, ສາທາລະນະລັດປະຊາທິປະໄຕກົງໂກ, ອູການດາແລະທິດຕາເວັນຕົກ Kenya. ຖິ່ນທີ່ຢູ່ອາໄສປະກອບດ້ວຍພື້ນທີ່ເປີດໃນປ່າຊຸ່ມແລະມີຝາປິດ.
Caleta caleta: Caleta caleta , ຮູບສີ່ ຫລ່ຽມທີ່ ເປັນຮູບສີ່ ຫລ່ຽມ , ເປັນຊະນິດຂອງຜີເສື້ອສີຟ້າທີ່ພົບໃນ Sulawesi.
ຫິນອ່ອນ Lythrum alatum, ເປັນທີ່ຮູ້ຈັກທົ່ວໄປເປັນ loosestrife ໄຂບໍ່ໄດ້, lythrum ມີປີກຫຼືເປັນລ່ຽມສີມ່ວງ, loosestrife, ເປັນຊະນິດຂອງການອອກດອກພືດທີ່ເປັນຂອງຄອບຄົວ Lythraceae ໄດ້. ມັນແຜ່ຂະຫຍາຍໄປທົ່ວເຂດດິນທາມໃນພາກກາງແລະພາກຕາເວັນອອກຂອງສະຫະລັດແລະ Ontario.
ຊີວະປະຫວັດ Epioblasma: Epioblasma biemarginata , riffleshell ມຸມ ເປັນຊະນິດຂອງ mussel ນ້ໍາຈືດ, ເປັນ mollusk bivalve ສັດນ້ໍາໃນຄອບຄົວ Unionidae, mussels ນ້ໍາ. ດຽວນີ້ມັນສູນພັນໄປແລ້ວ.
ອຽງແກນ: ໃນດາລາສາດ, ການອຽງທາງແກນ , ເຊິ່ງເອີ້ນກັນວ່າ obliquity , ແມ່ນມຸມລະຫວ່າງແກນ ໝູນ ວຽນຂອງວັດຖຸແລະແກນວົງໂຄຈອນຂອງມັນ, ຫຼືເທົ່າກັນ, ມຸມລະຫວ່າງຍົນສົມຜົນຂອງມັນແລະກັບວົງໂຄຈອນ. ມັນແຕກຕ່າງກັບແນວໂນ້ມຂອງວົງໂຄຈອນ.
ໂຣດໂດ: Rhododon , ທີ່ເອີ້ນວ່າ sandmint, ແມ່ນສະກຸນຂອງຕົ້ນດອກໄມ້ໃນຄອບຄົວ Lamiaceae, ໄດ້ຖືກອະທິບາຍວ່າເປັນສະກຸນໃນປີ 1939. ມັນມີພຽງແຕ່ຊະນິດທີ່ຮູ້ຈັກກັນ, Rhododon ciliatus , ລັດ Texas sandmint ແຜ່ລາມ ໄປຫາລັດ Texas ໃນສະຫະລັດ.
Anteos maerula: Anteos maerula , ຊູນຟູຣິກ ຫລື ມຸມຊູນຟູຣິກ , ສີສົ້ມ , ແມ່ນຜີເສື້ອຂອງຄອບຄົວ Pieridae. ມັນໄດ້ຖືກພົບເຫັນຈາກປະເທດເປຣູກັບເມັກຊິໂກ. ເປັນສິ່ງທີ່ຫາຍາກ, ຜູ້ອົບພະຍົບສາມາດພົບເຫັນຢູ່ທາງທິດຕາເວັນອອກຂອງ Nebraska, ທິດຕາເວັນອອກສຽງໃຕ້ Arizona, ທິດຕາເວັນຕົກສຽງໃຕ້ຂອງ New Mexico, ພາກໃຕ້ຂອງ Texas, ລັດ Mississippi ແລະ Florida.
Curetis acuta: Curetis acuta , ແສງຕາເວັນທີ່ ມີມຸມ ເປັນປະເພດຂອງ butterfly ແມ່ນຂອງຄອບຄົວ lycaenid. ມັນໄດ້ຖືກພົບເຫັນຢູ່ໃນພົບພູມ Indomalayan. Curetis acuta ແມ່ນສີມ້ວງທາງເພດເນື່ອງຈາກມີສີສັນທີ່ແຕກຕ່າງກັນຂອງປີກລະຫວ່າງເພດ, ແຕ່ວ່າປີກຂອງມັນທີ່ຄ້າຍຄືກັນແລະສີເງິນທີ່ສະທ້ອນແສງແດດ. ການສະທ້ອນແສງສະຫວ່າງໂດຍປີກດອກໄມ້ເງິນມີບົດບາດໃນການສັນຍານໃນລະຫວ່າງການບິນ, ການປຸ່ງແຕ່ງໃນເວລາທີ່ພັກຜ່ອນຫຼືໃນຊ່ວງເວລາ hibernation, ແລະອຸນຫະພູມໃນຮ່າງກາຍຫຼຸດລົງໂດຍການສະທ້ອນແສງແດດ
ເສືອໂຄ້ງ: ເສືອທີ່ ມີຮູບສີ່ຫລ່ຽມແມ່ນສາຍພັນຂອງຜີເສື້ອຜີວ ໜັງ Nymphalid ທີ່ຢູ່ໃນແດນ Danainae ມັນພົບຢູ່ Papua New Guinea ແລະເກາະ Solomon.
Scopula ancellata: Scopula ancellata , ຄື້ນຟອງທີ່ເປັນມຸມ ຫຼື ຄື້ນທີ່ມີປີກທີ່ມີປີກ , ແມ່ນແມງກະເບື້ອຂອງຄອບຄົວ Geometridae. ມັນໄດ້ຖືກອະທິບາຍໂດຍ George Duryea Hulst ໃນປີ 1887. ມັນໄດ້ຖືກພົບເຫັນຢູ່ໃນອາເມລິກາເຫນືອຈາກ Quebec ທິດຕາເວັນຕົກເຖິງເຂດຕາເວັນຕົກສຽງ ເໜືອ ແລະອັງກິດ Columbia ແລະທິດໃຕ້ເຖິງ Michigan, Indiana ແລະ Arizona. ຖິ່ນທີ່ຢູ່ອາໄສປະກອບດ້ວຍໄມ້ປະສົມແລະປ່າໄມ້ທີ່ມີຊີວິດຊີວາ.
Scopula ancellata: Scopula ancellata , ຄື້ນຟອງທີ່ເປັນມຸມ ຫຼື ຄື້ນທີ່ມີປີກທີ່ມີປີກ , ແມ່ນແມງກະເບື້ອຂອງຄອບຄົວ Geometridae. ມັນໄດ້ຖືກອະທິບາຍໂດຍ George Duryea Hulst ໃນປີ 1887. ມັນໄດ້ຖືກພົບເຫັນຢູ່ໃນອາເມລິກາເຫນືອຈາກ Quebec ທິດຕາເວັນຕົກເຖິງເຂດຕາເວັນຕົກສຽງ ເໜືອ ແລະອັງກິດ Columbia ແລະທິດໃຕ້ເຖິງ Michigan, Indiana ແລະ Arizona. ຖິ່ນທີ່ຢູ່ອາໄສປະກອບດ້ວຍໄມ້ປະສົມແລະປ່າໄມ້ທີ່ມີຊີວິດຊີວາ.
Tellina gaimardi: Tellina gaimardi , ຫອຍນາງລົມ ເປັນ ລ່ຽມ , ແມ່ນສາຍພັນຫລໍ່ຂອງຄອບຄົວ Tellinidae.
ແລນແລນແມ່ທ້ອງ: ແລນ ດາງເປັນລາກແມ່ນສັດຊະນິດສັດເລືອຄານໃນ Trogonophidae ໃນຄອບຄົວ. ມັນຖືກພົບເຫັນຢູ່ໃນໂຊມາເລຍໃນ Horn of Africa.
Angledool: Angledool ແມ່ນທ້ອງຖິ່ນໃນພາກຕາເວັນຕົກສ່ຽງ ເໜືອ New South Wales ໃກ້ກັບຊາຍແດນທາງໃຕ້ຂອງລັດ Queensland, ໜຶ່ງ ກິໂລແມັດທາງຕາເວັນອອກຂອງຖະ ໜົນ Castreagh ແລະປະມານ 45 ກິໂລແມັດທາງ ເໜືອ ຂອງ Lightning Ridge. ໃນການ ສຳ ຫຼວດພົນລະເມືອງປີ 2016, Angledool ມີປະຊາກອນທັງ ໝົດ 58 ຄົນ.