Abstract analytic number theory, Arithmetic progression, Arithmetic progression

ທິດສະດີເລກວິເຄາະ ທິດສະດີ ການຄິດໄລ່ເລກ ເສີຍໆ ແມ່ນສາຂາຂອງຄະນິດສາດເຊິ່ງໃຊ້ແນວຄວາມຄິດແລະເຕັກນິກຂອງທິດສະດີເລກຄິດໄລ່ແບບຄລາສສິກແລະ ນຳ ໃຊ້ພວກມັນເຂົ້າໃນຂົງເຂດຄະນິດສາດທີ່ແຕກຕ່າງກັນ. ທິດສະດີບົດເລກ ທຳ ອິດແມ່ນປະຕິບັດຕົວຢ່າງຕົ້ນແບບ, ແລະການເນັ້ນ ໜັກ ແມ່ນຜົນໄດ້ຮັບການແຈກຢາຍແບບບໍ່ມີຕົວຕົນ. ທິດສະດີດັ່ງກ່າວໄດ້ຖືກປະດິດຂື້ນແລະພັດທະນາໂດຍນັກຄະນິດສາດເຊັ່ນ John Knopfmacher ແລະ Arne Beurling ໃນສະຕະວັດທີ 20.
ຄວາມຄືບ ໜ້າ ເລກຄະນິດສາດ: ຄວາມຄືບ ໜ້າ ກ່ຽວກັບເລກຄະນິດສາດ (AP) ຫຼື ລຳ ດັບເລກຄະນິດສາດ ແມ່ນ ລຳ ດັບຂອງຕົວເລກດັ່ງກ່າວວ່າຄວາມແຕກຕ່າງລະຫວ່າງ ຄຳ ຕໍ່ເນື່ອງແມ່ນຄົງທີ່. ຍົກຕົວຢ່າງ, ລຳ ດັບ 5, 7, 9, 11, 13, 15,. .. ແມ່ນຄວາມຄືບ ໜ້າ ເລກຄະນິດສາດທີ່ມີຄວາມແຕກຕ່າງທົ່ວໄປຂອງ 2.
ຄວາມຄືບ ໜ້າ ເລກຄະນິດສາດ: ຄວາມຄືບ ໜ້າ ກ່ຽວກັບເລກຄະນິດສາດ (AP) ຫຼື ລຳ ດັບເລກຄະນິດສາດ ແມ່ນ ລຳ ດັບຂອງຕົວເລກດັ່ງກ່າວວ່າຄວາມແຕກຕ່າງລະຫວ່າງ ຄຳ ຕໍ່ເນື່ອງແມ່ນຄົງທີ່. ຍົກຕົວຢ່າງ, ລຳ ດັບ 5, 7, 9, 11, 13, 15,. .. ແມ່ນຄວາມຄືບ ໜ້າ ເລກຄະນິດສາດທີ່ມີຄວາມແຕກຕ່າງທົ່ວໄປຂອງ 2.
ທີ່ກໍານົດໄວ້ເລກຄະນິດສາດ: ໃນເຫດຜົນທາງຄະນິດສາດ, ຊຸດ ເລກຄະນິດສາດ ແມ່ນຕົວເລກ ທຳ ມະຊາດທີ່ສາມາດ ກຳ ນົດໄດ້ໂດຍສູດຂອງເລກຄະນິດສາດ Peano ທຳ ອິດ. ຊຸດກ່ຽວກັບເລກຄະນິດສາດໄດ້ຖືກຈັດແບ່ງຕາມ ລຳ ດັບຊັ້ນເລກຄະນິດສາດ.
ການປ່ຽນແປງເລກຄະນິດສາດ: ໃນການຂຽນໂປແກຼມຄອມພິວເຕີ້, ການ ປ່ຽນເລກຄະນິດສາດ ແມ່ນຜູ້ປະຕິບັດການປ່ຽນແປງ, ບາງຄັ້ງກໍ່ເອີ້ນວ່າການ ປ່ຽນແປງທີ່ເຊັນ . ສອງປະເພດພື້ນຖານແມ່ນການ ເລື່ອນຊ້າຍດ້ານເລກເລກ ແລະການ ເລື່ອນຂວາດ້ານເລກເລກ . ສຳ ລັບຕົວເລກຖານສອງມັນແມ່ນການ ດຳ ເນີນງານທີ່ມີຄວາມ ໝາຍ ເລັກນ້ອຍເຊິ່ງປ່ຽນສ່ວນທັງ ໝົດ ຂອງ ລຳ ດັບຂອງມັນ; ທຸກໆບິດໃນລະຄອນພຽງແຕ່ຍ້າຍ ຈຳ ນວນ ຕຳ ແໜ່ງ ນ້ອຍໆ, ແລະ ຕຳ ແໜ່ງ bit-vacant ທີ່ເຕັມໄປດ້ວຍ. ແທນທີ່ຈະເຕັມໄປດ້ວຍ 0s ທັງ ໝົດ, ຄືກັບການປ່ຽນທິດທາງທີ່ສົມເຫດສົມຜົນ, ເມື່ອປ່ຽນໄປທາງຂວາ, ສ່ວນທາງຊ້າຍແມ່ນຖືກປ່ຽນເປັນ ຕື່ມທຸກ ຕຳ ແໜ່ງ ທີ່ວ່າງ.
ການຄິດໄລ່ທາງຈິດ: ການຄິດໄລ່ທາງຈິດ ປະກອບດ້ວຍການຄິດໄລ່ເລກຄະນິດສາດໂດຍໃຊ້ສະ ໝອງ ຂອງມະນຸດເທົ່ານັ້ນ, ໂດຍບໍ່ມີການຊ່ວຍເຫຼືອຈາກອຸປະກອນຫຼືອຸປະກອນໃດ ໜຶ່ງ ເຊັ່ນເຄື່ອງຄິດໄລ່. ປະຊາຊົນໃຊ້ການຄິດໄລ່ດ້ານຈິດໃຈໃນເວລາທີ່ເຄື່ອງມືຄອມພິວເຕີ້ບໍ່ມີ, ເມື່ອມັນໄວກ່ວາວິທີການຄິດໄລ່ອື່ນໆ, ຫຼືແມ່ນແຕ່ໃນສະພາບການແຂ່ງຂັນ. ການຄິດໄລ່ທາງຈິດມັກກ່ຽວຂ້ອງກັບການ ນຳ ໃຊ້ເຕັກນິກສະເພາະທີ່ຖືກສ້າງຂື້ນ ສຳ ລັບບັນຫາສະເພາະ. ຄົນທີ່ມີຄວາມສາມາດສູງໃນການຄິດໄລ່ຈິດໃຈຜິດປົກກະຕິຖືກເອີ້ນວ່າເຄື່ອງຄິດໄລ່ທາງຈິດຫຼື ເຄື່ອງຄິດໄລ່ຟ້າຜ່າ s.
ການຄິດໄລ່ທາງຈິດ: ການຄິດໄລ່ທາງຈິດ ປະກອບດ້ວຍການຄິດໄລ່ເລກຄະນິດສາດໂດຍໃຊ້ສະ ໝອງ ຂອງມະນຸດເທົ່ານັ້ນ, ໂດຍບໍ່ມີການຊ່ວຍເຫຼືອຈາກອຸປະກອນຫຼືອຸປະກອນໃດ ໜຶ່ງ ເຊັ່ນເຄື່ອງຄິດໄລ່. ປະຊາຊົນໃຊ້ການຄິດໄລ່ດ້ານຈິດໃຈໃນເວລາທີ່ເຄື່ອງມືຄອມພິວເຕີ້ບໍ່ມີ, ເມື່ອມັນໄວກ່ວາວິທີການຄິດໄລ່ອື່ນໆ, ຫຼືແມ່ນແຕ່ໃນສະພາບການແຂ່ງຂັນ. ການຄິດໄລ່ທາງຈິດມັກກ່ຽວຂ້ອງກັບການ ນຳ ໃຊ້ເຕັກນິກສະເພາະທີ່ຖືກສ້າງຂື້ນ ສຳ ລັບບັນຫາສະເພາະ. ຄົນທີ່ມີຄວາມສາມາດສູງໃນການຄິດໄລ່ຈິດໃຈຜິດປົກກະຕິຖືກເອີ້ນວ່າເຄື່ອງຄິດໄລ່ທາງຈິດຫຼື ເຄື່ອງຄິດໄລ່ຟ້າຜ່າ s.
ຄວາມແຂງແຮງ: ໃນເຫດຜົນ, ມີຄວາມຊັດເຈນກວ່າໃນການຫາເຫດຜົນທີ່ສາມາດຕັດໄດ້, ການໂຕ້ຖຽງແມ່ນ ສຽງ ຖ້າມັນມີທັງຮູບແບບແລະສະຖານທີ່ຂອງມັນແມ່ນຄວາມຈິງ. ສຽງແມ່ນຍັງມີຄວາມ ໝາຍ ທີ່ກ່ຽວຂ້ອງກັບທາງດ້ານຄະນິດສາດ, ໃນນັ້ນລະບົບທີ່ມີເຫດຜົນແມ່ນດີຖ້າແລະຖ້າວ່າທຸກໆສູດທີ່ສາມາດພິສູດໄດ້ໃນລະບົບແມ່ນມີເຫດຜົນຢ່າງຖືກຕ້ອງໂດຍອີງໃສ່ semantics ຂອງລະບົບ.
ກ້ຽວວຽນ Archimedean: ກ້ຽວວຽນ Archimedean ແມ່ນກ້ຽວວຽນທີ່ມີຊື່ຕາມສະກຸນ Archimedes ນັກຄະນິດສາດເຣັກໃນສະຕະວັດທີ 3 BC ມັນແມ່ນສະຖານທີ່ທີ່ສອດຄ້ອງກັບສະຖານທີ່ຕ່າງໆຕາມການເວລາຂອງຈຸດທີ່ຍ້າຍອອກໄປຈາກຈຸດຄົງທີ່ທີ່ມີຄວາມໄວຄົງທີ່ຕາມເສັ້ນທີ່ ໝຸນ ກັບຄວາມໄວຂອງມຸມ. ຢ່າງເທົ່າທຽມກັນ, ໃນການປະສານງານຂົ້ວໂລກ ( r , θ ) ມັນສາມາດຖືກອະທິບາຍໂດຍສົມຜົນ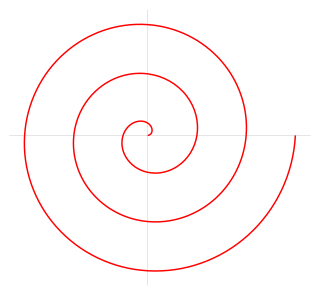
ກຸ່ມເລກຄະນິດສາດ: ໃນຄະນິດສາດ, ກຸ່ມເລກຄະນິດສາດ ແມ່ນກຸ່ມ ໜຶ່ງ ທີ່ໄດ້ຮັບເປັນຈຸດບວກຂອງກຸ່ມພຶດຊະຄະນິດ, ຕົວຢ່າງ ພວກມັນເກີດຂື້ນຕາມ ທຳ ມະຊາດໃນການສຶກສາກ່ຽວກັບຄຸນສົມບັດເລກຄະນິດຂອງຮູບແບບສີ່ຫລ່ຽມແລະຫົວຂໍ້ຄລາສສິກອື່ນໆໃນທິດສະດີເລກ. ພວກເຂົາຍັງໃຫ້ຕົວຢ່າງທີ່ຫນ້າສົນໃຈຫຼາຍກ່ຽວກັບ manifolds Riemannian ແລະເພາະສະນັ້ນຈຶ່ງແມ່ນວັດຖຸທີ່ສົນໃຈກ່ຽວກັບເລຂາຄະນິດແລະ topology. ສຸດທ້າຍ, ສອງຫົວຂໍ້ນີ້ເຂົ້າຮ່ວມໃນທິດສະດີຂອງຮູບແບບອັດຕະໂນມັດເຊິ່ງເປັນພື້ນຖານໃນທິດສະດີເລກທັນສະ ໄໝ.
ຄວາມຄືບ ໜ້າ ເລກຄະນິດສາດ: ຄວາມຄືບ ໜ້າ ກ່ຽວກັບເລກຄະນິດສາດ (AP) ຫຼື ລຳ ດັບເລກຄະນິດສາດ ແມ່ນ ລຳ ດັບຂອງຕົວເລກດັ່ງກ່າວວ່າຄວາມແຕກຕ່າງລະຫວ່າງ ຄຳ ຕໍ່ເນື່ອງແມ່ນຄົງທີ່. ຍົກຕົວຢ່າງ, ລຳ ດັບ 5, 7, 9, 11, 13, 15,. .. ແມ່ນຄວາມຄືບ ໜ້າ ເລກຄະນິດສາດທີ່ມີຄວາມແຕກຕ່າງທົ່ວໄປຂອງ 2.
ດ້ານເລກຄະນິດສາດ: ໃນຄະນິດສາດ, ພື້ນຜິວເລກຄະນິດສາດ ເໜືອ ໂດເມນ Dedekind R ທີ່ມີສ່ວນປະກອບ ແມ່ນວັດຖຸເລຂາຄະນິດທີ່ມີມິຕິ ທຳ ມະດາ ໜຶ່ງ ໜ່ວຍ, ແລະອີກ ໜຶ່ງ ມິຕິອື່ນທີ່ສະ ໜອງ ໂດຍນິຍາມຂອງນາຍົກລັດຖະມົນຕີ. ໃນເວລາທີ່ R ແມ່ນແຫວນຂອງເລກເຕັມ Z , ຄວາມຕັ້ງໃຈນີ້ຂື້ນກັບລະດັບທີ່ດີທີ່ສຸດ ສຳ ລັບລະດັບສະເພາະ ( Z ) ທີ່ຖືກເຫັນວ່າປຽບທຽບກັບເສັ້ນ. ພື້ນຜິວກ່ຽວກັບເລກຄະນິດສາດເກີດຂື້ນຕາມ ທຳ ມະຊາດໃນເລຂາຄະນິດ diophantine, ເມື່ອເສັ້ນໂຄ້ງຂອງພຶດຊະຄະນິດໃນ K ຖືກຄິດວ່າມີການຫຼຸດລົງໃນພື້ນທີ່ R / P , ບ່ອນທີ່ P ແມ່ນສິ່ງທີ່ດີທີ່ສຸດຂອງ R , ສຳ ລັບເກືອບທັງ ໝົດ P ; ແລະມີປະໂຫຍດໃນການລະບຸສິ່ງທີ່ຄວນຈະເກີດຂື້ນກ່ຽວກັບຂະບວນການຫຼຸດລົງເປັນ R / P ເມື່ອວິທີການທີ່ໂງ່ທີ່ສຸດເຮັດໃຫ້ບໍ່ມີຄວາມ ໝາຍ.
ເລກຄະນິດສາດ: Topology ກ່ຽວກັບເລກຄະນິດສາດ ແມ່ນພື້ນທີ່ຂອງຄະນິດສາດເຊິ່ງເປັນການລວມຕົວຂອງທິດສະດີຄະນິດສາດແລະເລກທະເລ. ມັນສ້າງຄວາມຄ້າຍຄືກັນລະຫວ່າງຂົງເຂດ ຈຳ ນວນແລະປິດ, 3 ຮູບແບບນິຍົມ.
ແຜນວາດ Coxeter – Dynkin: ໃນຮູບເລຂາຄະນິດ, ແຜນວາດ Coxeter – Dynkin ແມ່ນເສັ້ນສະແດງທີ່ມີຂອບ ໝາຍ ທີ່ມີປ້າຍຊື່ເປັນຕົວແທນຂອງຄວາມ ສຳ ພັນທາງກວ້າງລະຫວ່າງການເກັບ ກຳ ກະຈົກ. ມັນອະທິບາຍເຖິງການກໍ່ສ້າງ kaleidoscopic: ແຕ່ລະເສັ້ນສະແດງ "node" ເປັນຕົວແທນຂອງກະຈົກແລະປ້າຍທີ່ຕິດກັບສາຂາເຂົ້າລະຫັດ ຄຳ ສັ່ງມຸມຂອງໂບດລະຫວ່າງສອງກະຈົກ, ນັ້ນແມ່ນ ຈຳ ນວນເງິນທີ່ມຸມລະຫວ່າງຍົນສະທ້ອນແສງສາມາດຄູນດ້ວຍເພື່ອໃຫ້ໄດ້ 180 ອົງສາ. ສາຂາທີ່ບໍ່ມີປ້າຍຊື່ຢ່າງຊັດເຈນສະແດງເຖິງ ຄຳ ສັ່ງເລກທີ 3.
underith ເລກຄະນິດສາດ: ຄຳ ວ່າ ເລກຄະນິດສາດ underflow ແມ່ນເງື່ອນໄຂໃນໂປຣແກຣມຄອມພິວເຕີເຊິ່ງຜົນຂອງການ ຄຳ ນວນແມ່ນ ຈຳ ນວນນ້ອຍທີ່ມີຄ່ານ້ອຍກວ່າຄອມພິວເຕີ້ສາມາດເປັນຕົວແທນໃນຫນ່ວຍຄວາມ ຈຳ ໃນ ໜ່ວຍ ປະມວນຜົນສູນກາງ (CPU) ຂອງມັນ.
ແນວພັນເລກຄະນິດສາດ: ໃນຄະນິດສາດ, ຄວາມ ຫຼາກຫຼາຍກ່ຽວກັບເລກຄະນິດສາດ ແມ່ນພື້ນທີ່ທີ່ມີຂະ ໜາດ ເທົ່າທຽມກັນຂອງກຸ່ມສົມມະຕິເລກ Hermitian ໂດຍກຸ່ມຍ່ອຍກ່ຽວກັບເລກຄະນິດສາດຂອງກຸ່ມກ່ຽວກັບພຶດຊະຄະນິດ.
ແນວພັນເລກຄະນິດສາດ: ໃນຄະນິດສາດ, ຄວາມ ຫຼາກຫຼາຍກ່ຽວກັບເລກຄະນິດສາດ ແມ່ນພື້ນທີ່ທີ່ມີຂະ ໜາດ ເທົ່າທຽມກັນຂອງກຸ່ມສົມມະຕິເລກ Hermitian ໂດຍກຸ່ມຍ່ອຍກ່ຽວກັບເລກຄະນິດສາດຂອງກຸ່ມກ່ຽວກັບພຶດຊະຄະນິດ.
ຫນ້າທີ່ zeta ກ່ຽວກັບເລກຄະນິດສາດ: ໃນຄະນິດສາດ, ໜ້າ ທີ່ zeta ເລກຄະນິດສາດ ແມ່ນ ໜ້າ ທີ່ຂອງ zeta ທີ່ກ່ຽວຂ້ອງກັບລະບົບປະເພດທີ່ມີລະດັບ ຈຳ ນວນເກີນ ຈຳ ນວນ. ຫນ້າທີ່ zeta ກ່ຽວກັບເລກຄະນິດສາດໂດຍທົ່ວໄປແລ້ວແມ່ນ ໜ້າ ທີ່ຂອງ Riemann zeta ແລະ Dedekind zeta ໃນຂະ ໜາດ ທີ່ສູງກວ່າ. ຫນ້າທີ່ zeta ເລກຄະນິດສາດແມ່ນ ໜຶ່ງ ໃນບັນດາວັດຖຸພື້ນຖານທີ່ສຸດຂອງທິດສະດີເລກ.
Arithmetica: Arithmetica ແມ່ນຕົວ ໜັງ ສືເຣັກບູຮານກ່ຽວກັບຄະນິດສາດທີ່ຂຽນໂດຍນັກຄະນິດສາດ Diophantus ໃນສະຕະວັດທີ 3 AD. ມັນເປັນການລວບລວມຂອງ 130 ບັນຫາກ່ຽວກັບພຶດຊະຄະນິດໃຫ້ວິທີແກ້ໄຂຕົວເລກຂອງການ ກຳ ນົດສົມຜົນແລະສົມຜົນທີ່ບໍ່ໄດ້ ກຳ ນົດ.
John Wallis: John Wallis ແມ່ນນັກບວດອັງກິດແລະນັກຄະນິດສາດທີ່ໄດ້ຮັບກຽດຕິຍົດບາງສ່ວນ ສຳ ລັບການພັດທະນາການຄິດໄລ່ infinitesimal. ໃນລະຫວ່າງປີ 1643 ເຖິງປີ 1689 ທ່ານໄດ້ ດຳ ລົງ ຕຳ ແໜ່ງ ເປັນຫົວ ໜ້າ ນັກສະແດງລະຫັດ ສຳ ລັບລັດຖະສະພາແລະຕໍ່ມາສານລາດຊະ ສຳ ນັກ ລາວໄດ້ຮັບການຍົກຍ້ອງດ້ວຍການແນະ ນຳ ສັນຍາລັກ∞ເພື່ອເປັນຕົວແທນແນວຄວາມຄິດຂອງຄວາມເປັນນິດ. ລາວຄ້າຍຄືກັນໃຊ້ 1 / ∞ ສຳ ລັບຄົນທີ່ບໍ່ມີຂອບເຂດ. John Wallis ແມ່ນຍຸກສະ ໄໝ ໃໝ່ ຂອງ Newton ແລະແມ່ນ ໜຶ່ງ ໃນບັນດານັກປັນຍາຊົນທີ່ຍິ່ງໃຫຍ່ທີ່ສຸດໃນການຄົ້ນຄວ້າ ໃໝ່ ຂອງຄະນິດສາດ.
Henry Briggs (ນັກຄະນິດສາດ): Henry Briggs ແມ່ນນັກຄະນິດສາດພາສາອັງກິດທີ່ມີຄວາມໂດດເດັ່ນໃນການປ່ຽນແປງພາສາຕົ້ນສະບັບທີ່ຖືກປະດິດໂດຍ John Napier ເຂົ້າໄປໃນ logarithms ທົ່ວໄປ, ເຊິ່ງບາງຄັ້ງກໍ່ເອີ້ນວ່າ logarithms Briggsian ໃນກຽດຕິຍົດຂອງລາວ. ສູດການຄິດໄລ່ສະເພາະ ສຳ ລັບການແບ່ງແຍກຍາວນານໃນການ ນຳ ໃຊ້ທີ່ທັນສະ ໄໝ ໄດ້ຖືກແນະ ນຳ ໂດຍ Briggs c. 1600 AD.
Arithmetica Universalis: Arithmetica Universalis ແມ່ນບົດເລື່ອງຄະນິດສາດໂດຍ Isaac Newton. ຂຽນເປັນພາສາລາຕິນ, ມັນຖືກດັດແກ້ແລະຈັດພີມມາໂດຍ William Whiston, ຜູ້ສືບທອດຂອງ Newton ເປັນ Lucasian ອາຈານຄະນິດສາດທີ່ມະຫາວິທະຍາໄລ Cambridge. Arithmetica ແມ່ນອີງໃສ່ບັນທຶກການບັນຍາຍຂອງ Newton.
ສິບແຄນຄອມພິວເຕີ້: ສິບຫລ່ຽມ ຄຳ ແມ່ນການລວບລວມສິບຜົນງານທາງຄະນິດສາດຂອງຈີນ, ລວບລວມໂດຍນັກເລຂາຄະນິດສາດຊັ້ນຕົ້ນ Li Chunfeng (602–670), ເປັນບົດເລື່ອງທາງຄະນິດສາດຢ່າງເປັນທາງການ ສຳ ລັບການກວດກາຄວາມສົມບູນທາງດ້ານຄະນິດສາດ.
ເລກຄະນິດສາດທີສອງ: ໃນເຫດຜົນທາງຄະນິດສາດ, ເລກຄະນິດສາດທີສອງ ແມ່ນການລວບລວມຂອງລະບົບ axiomatic ທີ່ເຮັດໃຫ້ຕົວເລກ ທຳ ມະຊາດແລະ ຈຳ ນວນຂອງມັນເປັນທາງການ. ມັນເປັນທາງເລືອກ ໜຶ່ງ ສຳ ລັບທິດສະດີທີ່ຕັ້ງເປັນ axiomatic ເປັນພື້ນຖານ ສຳ ລັບຄະນິດສາດ.
George Peacock: George Peacock FRS ແມ່ນນັກຄະນິດສາດອັງກິດແລະນັກບວດອັງກິດ. ລາວໄດ້ສ້າງຕັ້ງສິ່ງທີ່ເອີ້ນວ່າຄະນິດສາດຂອງອັງກິດ.
ເລຂາຄະນິດກ່ຽວກັບເລກຄະນິດສາດ: ໃນຄະນິດສາດ, ເລຂາຄະນິດສາດ ແມ່ນປະມານການ ນຳ ໃຊ້ເຕັກນິກຈາກເລຂາຄະນິດຄະນິດສາດເຖິງບັນຫາໃນທິດສະດີເລກ. ເລຂາຄະນິດກ່ຽວກັບເລກຄະນິດສາດແມ່ນເປັນຈຸດສູນກາງປະມານເລຂາຄະນິດ Diophantine, ການສຶກສາຈຸດທີ່ສົມເຫດສົມຜົນຂອງແນວພັນພຶດຊະຄະນິດ.
ໜ່ວຍ ງານຕາມເຫດຜົນເລກຄະນິດສາດ: ໃນການຄິດໄລ່ຄອມພິວເຕີ້, ໜ່ວຍ ງານຕາມເຫດຜົນກ່ຽວກັບເລກຄະນິດສາດ (ALU) ແມ່ນວົງຈອນດິຈິຕອນປະສົມປະສານທີ່ເຮັດ ໜ້າ ທີ່ກ່ຽວກັບເລກຄະນິດສາດແລະຂີດຕໍ່ເລກຖານສອງ. ນີ້ແມ່ນກົງກັນຂ້າມກັບ ໜ່ວຍ ລອຍນໍ້າຈຸດ (FPU), ເຊິ່ງ ດຳ ເນີນການກັບຕົວເລກຈຸດລອຍ. ມັນແມ່ນສິ່ງກໍ່ສ້າງພື້ນຖານຂອງວົງຈອນຄອມພິວເຕີ້ຫລາຍປະເພດ, ລວມທັງ ໜ່ວຍ ງານປະມວນຜົນສູນກາງ (CPU) ຂອງຄອມພິວເຕີ້, FPUs, ແລະ ໜ່ວຍ ປະມວນຜົນກາຟິກ (GPUs).
ເລກຄະນິດສາດທີສອງ: ໃນເຫດຜົນທາງຄະນິດສາດ, ເລກຄະນິດສາດທີສອງ ແມ່ນການລວບລວມຂອງລະບົບ axiomatic ທີ່ເຮັດໃຫ້ຕົວເລກ ທຳ ມະຊາດແລະ ຈຳ ນວນຂອງມັນເປັນທາງການ. ມັນເປັນທາງເລືອກ ໜຶ່ງ ສຳ ລັບທິດສະດີທີ່ຕັ້ງເປັນ axiomatic ເປັນພື້ນຖານ ສຳ ລັບຄະນິດສາດ.
ເລກຄະນິດສາດທີສອງ: ໃນເຫດຜົນທາງຄະນິດສາດ, ເລກຄະນິດສາດທີສອງ ແມ່ນການລວບລວມຂອງລະບົບ axiomatic ທີ່ເຮັດໃຫ້ຕົວເລກ ທຳ ມະຊາດແລະ ຈຳ ນວນຂອງມັນເປັນທາງການ. ມັນເປັນທາງເລືອກ ໜຶ່ງ ສຳ ລັບທິດສະດີທີ່ຕັ້ງເປັນ axiomatic ເປັນພື້ນຖານ ສຳ ລັບຄະນິດສາດ.
ທິດສະດີເລກວິເຄາະ ທິດສະດີ ການຄິດໄລ່ເລກ ເສີຍໆ ແມ່ນສາຂາຂອງຄະນິດສາດເຊິ່ງໃຊ້ແນວຄວາມຄິດແລະເຕັກນິກຂອງທິດສະດີເລກຄິດໄລ່ແບບຄລາສສິກແລະ ນຳ ໃຊ້ພວກມັນເຂົ້າໃນຂົງເຂດຄະນິດສາດທີ່ແຕກຕ່າງກັນ. ທິດສະດີບົດເລກ ທຳ ອິດແມ່ນປະຕິບັດຕົວຢ່າງຕົ້ນແບບ, ແລະການເນັ້ນ ໜັກ ແມ່ນຜົນໄດ້ຮັບການແຈກຢາຍແບບບໍ່ມີຕົວຕົນ. ທິດສະດີດັ່ງກ່າວໄດ້ຖືກປະດິດຂື້ນແລະພັດທະນາໂດຍນັກຄະນິດສາດເຊັ່ນ John Knopfmacher ແລະ Arne Beurling ໃນສະຕະວັດທີ 20.
ໜ້າ ທີ່ກ່ຽວກັບເລກຄະນິດສາດ: ໃນທິດສະດີ ຈຳ ນວນ, ຕຳ ແໜ່ງ ເລກຄະນິດສາດ , ເລກຄະນິດສາດ ຫລື ຈຳ ນວນທິດສະດີ ແມ່ນ ສຳ ລັບຜູ້ຂຽນສ່ວນຫຼາຍແມ່ນ ຕຳ ແໜ່ງ f ( n ) ທີ່ໂດເມນແມ່ນເລກບວກແລະ ຈຳ ນວນຂອງມັນແມ່ນ ຈຳ ນວນຍ່ອຍຂອງ ຈຳ ນວນສັບຊ້ອນ. Hardy & Wright ປະກອບມີໃນນິຍາມຂອງພວກເຂົາຄວາມຕ້ອງການທີ່ວ່າ ໜ້າ ທີ່ເລກຄະນິດສາດ "ສະແດງຄຸນສົມບັດເລກຄະນິດສາດຂອງ n ".
ໜ້າ ທີ່ກ່ຽວກັບເລກຄະນິດສາດ: ໃນທິດສະດີ ຈຳ ນວນ, ຕຳ ແໜ່ງ ເລກຄະນິດສາດ , ເລກຄະນິດສາດ ຫລື ຈຳ ນວນທິດສະດີ ແມ່ນ ສຳ ລັບຜູ້ຂຽນສ່ວນຫຼາຍແມ່ນ ຕຳ ແໜ່ງ f ( n ) ທີ່ໂດເມນແມ່ນເລກບວກແລະ ຈຳ ນວນຂອງມັນແມ່ນ ຈຳ ນວນຍ່ອຍຂອງ ຈຳ ນວນສັບຊ້ອນ. Hardy & Wright ປະກອບມີໃນນິຍາມຂອງພວກເຂົາຄວາມຕ້ອງການທີ່ວ່າ ໜ້າ ທີ່ເລກຄະນິດສາດ "ສະແດງຄຸນສົມບັດເລກຄະນິດສາດຂອງ n ".
ລຳ ດັບຊັ້ນເລກຄະນິດສາດ: ໃນທາງເລກຄະນິດສາດ, ລຳ ດັບຊັ້ນຄະນິດສາດ , ລຳ ດັບຊັ້ນ ເລກຄະນິດສາດ ຫຼື ລຳ ດັບຊັ້ນສູງ Kleene – Mostowski ແບ່ງອອກຊຸດບາງຢ່າງໂດຍອີງໃສ່ຄວາມສັບສົນຂອງສູດທີ່ ກຳ ນົດພວກມັນ. ຊຸດໃດກໍ່ຕາມທີ່ໄດ້ຮັບການຈັດປະເພດແມ່ນຖືກເອີ້ນວ່າ ເລກຄະນິດສາດ .
ເລກຄະນິດສາດ: ໃນຄະນິດສາດແລະສະຖິຕິ, ຄວາມ ໝາຍ ເລກຄະນິດສາດ , ຫຼືພຽງແຕ່ຄ່າສະເລ່ຍຫຼື ສະເລ່ຍ , ແມ່ນການລວມຕົວເລກຂອງຕົວເລກທີ່ແບ່ງຕາມການນັບຂອງຕົວເລກໃນການເກັບ. ການລວບລວມມັກຈະເປັນຊຸດຂອງຜົນຂອງການທົດລອງຫລືການສຶກສາການສັງເກດການ, ຫຼືມັກຈະເປັນຊຸດຂອງຜົນໄດ້ຮັບຈາກການ ສຳ ຫຼວດ. ຄຳ ວ່າ "ຄວາມ ໝາຍ ເລກຄະນິດສາດ" ແມ່ນມັກໃນບາງສະພາບການທາງຄະນິດສາດແລະສະຖິຕິ, ເພາະວ່າມັນຊ່ວຍແຍກແຍະມັນຈາກວິທີອື່ນເຊັ່ນ: ຄວາມ ໝາຍ ຂອງເລຂາຄະນິດແລະຄວາມ ໝາຍ ທີ່ກົມກຽວກັນ.
ທີ່ກໍານົດໄວ້ເລກຄະນິດສາດ: ໃນເຫດຜົນທາງຄະນິດສາດ, ຊຸດ ເລກຄະນິດສາດ ແມ່ນຕົວເລກ ທຳ ມະຊາດທີ່ສາມາດ ກຳ ນົດໄດ້ໂດຍສູດຂອງເລກຄະນິດສາດ Peano ທຳ ອິດ. ຊຸດກ່ຽວກັບເລກຄະນິດສາດໄດ້ຖືກຈັດແບ່ງຕາມ ລຳ ດັບຊັ້ນເລກຄະນິດສາດ.
ທີ່ກໍານົດໄວ້ເລກຄະນິດສາດ: ໃນເຫດຜົນທາງຄະນິດສາດ, ຊຸດ ເລກຄະນິດສາດ ແມ່ນຕົວເລກ ທຳ ມະຊາດທີ່ສາມາດ ກຳ ນົດໄດ້ໂດຍສູດຂອງເລກຄະນິດສາດ Peano ທຳ ອິດ. ຊຸດກ່ຽວກັບເລກຄະນິດສາດໄດ້ຖືກຈັດແບ່ງຕາມ ລຳ ດັບຊັ້ນເລກຄະນິດສາດ.
ເລກຄະນິດສາດ: Arithmetic ແມ່ນສາຂາຂອງຄະນິດສາດເຊິ່ງປະກອບດ້ວຍການສຶກສາຕົວເລກ, ໂດຍສະເພາະກ່ຽວກັບຄຸນລັກສະນະຂອງການ ດຳ ເນີນງານຕາມປະເພນີທີ່ມີຕໍ່ພວກມັນ - ເພີ່ມ, ການຫັກລົບ, ຄູນ, ການແບ່ງ, ການອອກ ກຳ ລັງກາຍແລະການສະກັດຮາກ. ຄະນິດສາດແມ່ນສ່ວນ ໜຶ່ງ ຂອງທິດສະດີ, ແລະທິດສະດີເລກໄດ້ຖືກພິຈາລະນາວ່າເປັນ ໜຶ່ງ ໃນການແບ່ງຂັ້ນເທິງຂອງຄະນິດສາດທີ່ທັນສະ ໄໝ, ພ້ອມດ້ວຍຄະນິດສາດ, ເລຂາຄະນິດແລະການວິເຄາະ. ຄຳ ສັບກ່ຽວກັບ ເລກຄະນິດສາດ ແລະ ເລກຄະນິດສາດ ສູງ ໄດ້ຖືກ ນຳ ໃຊ້ຈົນຮອດຕົ້ນສະຕະວັດທີ 20 ເປັນສັບຄ້າຍຄືກັນ ສຳ ລັບ ທິດສະດີເລກ , ແລະບາງຄັ້ງກໍ່ຍັງໃຊ້ເພື່ອອ້າງອີງເຖິງສ່ວນ ໜຶ່ງ ທີ່ກວ້າງຂວາງຂອງທິດສະດີເລກ.
ຄວາມຄືບ ໜ້າ ເລກຄະນິດສາດ: ຄວາມຄືບ ໜ້າ ກ່ຽວກັບເລກຄະນິດສາດ (AP) ຫຼື ລຳ ດັບເລກຄະນິດສາດ ແມ່ນ ລຳ ດັບຂອງຕົວເລກດັ່ງກ່າວວ່າຄວາມແຕກຕ່າງລະຫວ່າງ ຄຳ ຕໍ່ເນື່ອງແມ່ນຄົງທີ່. ຍົກຕົວຢ່າງ, ລຳ ດັບ 5, 7, 9, 11, 13, 15,. .. ແມ່ນຄວາມຄືບ ໜ້າ ເລກຄະນິດສາດທີ່ມີຄວາມແຕກຕ່າງທົ່ວໄປຂອງ 2.
Otonality ແລະ Utonality: Otonality ແລະ utonality ແມ່ນ ຄຳ ສັບທີ່ Harry Partch ແນະ ນຳ ເພື່ອອະທິບາຍ chords ທີ່ມີຫ້ອງຮຽນ pitch ແມ່ນຄວາມກົມກຽວຫລື subharmonics ຂອງໂຕນທີ່ມີການ ກຳ ນົດ (ຕົວຕົນ), ຕາມ ລຳ ດັບ. ສໍາລັບຕົວຢ່າງ: 1/1, 2/1, 3/1, ... ຫລື 1/1, 1/2, 1/3, .... Otonality ແມ່ນຊຸດຂອງຂຸມທີ່ສ້າງຂື້ນໂດຍປັດໃຈຕົວເລກ (... ຕົວຕົນ ) ... ຫຼາຍກວ່າຕົວເລກຄົງທີ່ໃນຕົວຫານ. ກົງກັນຂ້າມ, Utonality ແມ່ນການປີ້ນກັບກັນຂອງ Otonality, ຊຸດຂອງຂຸມທີ່ມີຕົວເລກຄົງທີ່ໃນຕົວເລກຕໍ່ກັບປັດໃຈຕົວເລກ ... ໃນຕົວຫານ.
ທີ່ກໍານົດໄວ້ເລກຄະນິດສາດ: ໃນເຫດຜົນທາງຄະນິດສາດ, ຊຸດ ເລກຄະນິດສາດ ແມ່ນຕົວເລກ ທຳ ມະຊາດທີ່ສາມາດ ກຳ ນົດໄດ້ໂດຍສູດຂອງເລກຄະນິດສາດ Peano ທຳ ອິດ. ຊຸດກ່ຽວກັບເລກຄະນິດສາດໄດ້ຖືກຈັດແບ່ງຕາມ ລຳ ດັບຊັ້ນເລກຄະນິດສາດ.
ລຳ ດັບຊັ້ນເລກຄະນິດສາດ: ໃນທາງເລກຄະນິດສາດ, ລຳ ດັບຊັ້ນຄະນິດສາດ , ລຳ ດັບຊັ້ນ ເລກຄະນິດສາດ ຫຼື ລຳ ດັບຊັ້ນສູງ Kleene – Mostowski ແບ່ງອອກຊຸດບາງຢ່າງໂດຍອີງໃສ່ຄວາມສັບສົນຂອງສູດທີ່ ກຳ ນົດພວກມັນ. ຊຸດໃດກໍ່ຕາມທີ່ໄດ້ຮັບການຈັດປະເພດແມ່ນຖືກເອີ້ນວ່າ ເລກຄະນິດສາດ .
ແຫວນເລກຄະນິດສາດ: ໃນພຶດຊະຄະນິດ, ວົງແຫວນການປ່ຽນແປງ R ຖືກກ່າວເຖິງດ້ວຍ ເລກຄະນິດສາດ ຖ້າມີເງື່ອນໄຂທຽບເທົ່າດັ່ງຕໍ່ໄປນີ້: ທ້ອງຖິ່ນ ຂອງ R ຢູ່ ແມ່ນແຫວນທີ່ບໍ່ມີສາຍ ສຳ ລັບທຸກໆຈຸດສູງສຸດທີ່ ເໝາະ ສົມ ຂອງ R. ສຳ ລັບອຸດົມການທັງ ໝົດ , ແລະ , ສຳ ລັບອຸດົມການທັງ ໝົດ , ແລະ ,
ທີ່ກໍານົດໄວ້ເລກຄະນິດສາດ: ໃນເຫດຜົນທາງຄະນິດສາດ, ຊຸດ ເລກຄະນິດສາດ ແມ່ນຕົວເລກ ທຳ ມະຊາດທີ່ສາມາດ ກຳ ນົດໄດ້ໂດຍສູດຂອງເລກຄະນິດສາດ Peano ທຳ ອິດ. ຊຸດກ່ຽວກັບເລກຄະນິດສາດໄດ້ຖືກຈັດແບ່ງຕາມ ລຳ ດັບຊັ້ນເລກຄະນິດສາດ.
ຄະນິດສາດປີ້ນກັບກັນ: ຄະນິດສາດປີ້ນກັບກັນ ແມ່ນໂຄງການທີ່ມີເຫດຜົນທາງຄະນິດສາດທີ່ຊອກຫາການ ກຳ ນົດທິດສະດີໃດທີ່ຕ້ອງການເພື່ອພິສູດທິດສະດີຄະນິດສາດ. ວິທີການນິຍາມຂອງມັນສາມາດຖືກອະທິບາຍໂດຍຫຍໍ້ເປັນ "ການຖອຍຫລັງຈາກທິດສະດີໄປສູ່ທິດສະດີ", ກົງກັນຂ້າມກັບການປະຕິບັດທາງຄະນິດສາດ ທຳ ມະດາທີ່ໄດ້ຮັບທິດສະດີຈາກອາຊີ. ມັນສາມາດໄດ້ຮັບການຄິດເປັນການຄົ້ນພົບເງື່ອນໄຂທີ່ຈໍາເປັນຈາກເງື່ອນໄຂທີ່ພຽງພໍ.
ທີ່ກໍານົດໄວ້ເລກຄະນິດສາດ: ໃນເຫດຜົນທາງຄະນິດສາດ, ຊຸດ ເລກຄະນິດສາດ ແມ່ນຕົວເລກ ທຳ ມະຊາດທີ່ສາມາດ ກຳ ນົດໄດ້ໂດຍສູດຂອງເລກຄະນິດສາດ Peano ທຳ ອິດ. ຊຸດກ່ຽວກັບເລກຄະນິດສາດໄດ້ຖືກຈັດແບ່ງຕາມ ລຳ ດັບຊັ້ນເລກຄະນິດສາດ.
ທີ່ກໍານົດໄວ້ເລກຄະນິດສາດ: ໃນເຫດຜົນທາງຄະນິດສາດ, ຊຸດ ເລກຄະນິດສາດ ແມ່ນຕົວເລກ ທຳ ມະຊາດທີ່ສາມາດ ກຳ ນົດໄດ້ໂດຍສູດຂອງເລກຄະນິດສາດ Peano ທຳ ອິດ. ຊຸດກ່ຽວກັບເລກຄະນິດສາດໄດ້ຖືກຈັດແບ່ງຕາມ ລຳ ດັບຊັ້ນເລກຄະນິດສາດ.
ໜ້າ ທີ່ຂອງ Dedekind: ໃນວິຊາຄະນິດສາດ, ໜ້າ ທີ່ ຂອງ Dedekind zeta ຂອງຂະ ແໜງ ເລກທີ່ເປັນພຶດຊະຄະນິດ K , ໂດຍທົ່ວໄປ ໝາຍ ເຖິງ ( K ( s ), ແມ່ນການເຮັດວຽກທົ່ວໄປຂອງ Riemann zeta. ມັນສາມາດຖືກ ກຳ ນົດເປັນຊຸດ Dirichlet, ມັນມີການຂະຫຍາຍຜະລິດຕະພັນ Euler, ມັນພໍໃຈກັບສົມຜົນທີ່ເປັນປະໂຫຍດ, ມັນມີການວິເຄາະຕໍ່ເນື່ອງຕໍ່ ໜ້າ ທີ່ meromorphic ໃນຍົນ C ທີ່ສັບສົນໂດຍມີພຽງເສົາງ່າຍໆທີ່ s = 1, ແລະຄ່າຂອງມັນ encode. ຂໍ້ມູນເລກຄະນິດສາດຂອງ K. ທິດສະດີ Riemann ຂະຫຍາຍໄດ້ລະບຸວ່າຖ້າ ζ K ( s ) = 0 ແລະ 0 <Re ( s ) <1, ຫຼັງຈາກນັ້ນ Re ( s ) = 1/2.
ຜູ້ ນຳ ດ້ານຄະນິດສາດ, nova methodo exposita: The 1889 treatise Arithmetices principia, nova methodo exposita ໂດຍ Giuseppe Peano ແມ່ນເອກະສານ seminal ທີ່ຢູ່ໃນເຫດຜົນທາງຄະນິດສາດແລະທິດສະດີທີ່ ກຳ ນົດໄວ້, ແນະ ນຳ ສິ່ງທີ່ປະຈຸບັນແມ່ນ axiomatization ມາດຕະຖານຂອງ ຈຳ ນວນ ທຳ ມະຊາດ, ແລະຮູ້ກັນວ່າ Peano axioms, ພ້ອມທັງມີບາງແນວຄິດທີ່ແຜ່ຂະຫຍາຍເຊັ່ນ: ເປັນສັນຍາລັກ ສຳ ລັບການ ດຳ ເນີນງານທີ່ ກຳ ນົດໄວ້ໃນຂັ້ນພື້ນຖານ∈, ⊂, ∩, ∪, ແລະ A - B.
ຜູ້ ນຳ ດ້ານຄະນິດສາດ, nova methodo exposita: The 1889 treatise Arithmetices principia, nova methodo exposita ໂດຍ Giuseppe Peano ແມ່ນເອກະສານ seminal ທີ່ຢູ່ໃນເຫດຜົນທາງຄະນິດສາດແລະທິດສະດີທີ່ ກຳ ນົດໄວ້, ແນະ ນຳ ສິ່ງທີ່ປະຈຸບັນແມ່ນ axiomatization ມາດຕະຖານຂອງ ຈຳ ນວນ ທຳ ມະຊາດ, ແລະຮູ້ກັນວ່າ Peano axioms, ພ້ອມທັງມີບາງແນວຄິດທີ່ແຜ່ຂະຫຍາຍເຊັ່ນ: ເປັນສັນຍາລັກ ສຳ ລັບການ ດຳ ເນີນງານທີ່ ກຳ ນົດໄວ້ໃນຂັ້ນພື້ນຖານ∈, ⊂, ∩, ∪, ແລະ A - B.
ເລກຄະນິດສາດ: Arithmetic ແມ່ນສາຂາຂອງຄະນິດສາດເຊິ່ງປະກອບດ້ວຍການສຶກສາຕົວເລກ, ໂດຍສະເພາະກ່ຽວກັບຄຸນລັກສະນະຂອງການ ດຳ ເນີນງານຕາມປະເພນີທີ່ມີຕໍ່ພວກມັນ - ເພີ່ມ, ການຫັກລົບ, ຄູນ, ການແບ່ງ, ການອອກ ກຳ ລັງກາຍແລະການສະກັດຮາກ. ຄະນິດສາດແມ່ນສ່ວນ ໜຶ່ງ ຂອງທິດສະດີ, ແລະທິດສະດີເລກໄດ້ຖືກພິຈາລະນາວ່າເປັນ ໜຶ່ງ ໃນການແບ່ງຂັ້ນເທິງຂອງຄະນິດສາດທີ່ທັນສະ ໄໝ, ພ້ອມດ້ວຍຄະນິດສາດ, ເລຂາຄະນິດແລະການວິເຄາະ. ຄຳ ສັບກ່ຽວກັບ ເລກຄະນິດສາດ ແລະ ເລກຄະນິດສາດ ສູງ ໄດ້ຖືກ ນຳ ໃຊ້ຈົນຮອດຕົ້ນສະຕະວັດທີ 20 ເປັນສັບຄ້າຍຄືກັນ ສຳ ລັບ ທິດສະດີເລກ , ແລະບາງຄັ້ງກໍ່ຍັງໃຊ້ເພື່ອອ້າງອີງເຖິງສ່ວນ ໜຶ່ງ ທີ່ກວ້າງຂວາງຂອງທິດສະດີເລກ.
ພື້ນຖານຂອງສິລະປະ: Arithmetic ຂອງ Robert Recorde : ຫຼື, ພື້ນຖານຂອງສິລະປະ ແມ່ນ ໜຶ່ງ ໃນປື້ມ ຕຳ ລາຮຽນພາສາອັງກິດທີ່ຖືກພິມ ທຳ ອິດກ່ຽວກັບເລກຄະນິດສາດແລະເປັນທີ່ນິຍົມທີ່ສຸດໃນເວລານັ້ນ. The Ground of Arts ໄດ້ປະ ກົດຕົວຢູ່ລອນດອນໃນປີ 1543, ແລະມັນໄດ້ຖືກພິມຄືນອີກປະມານ 45 ສະບັບອີກຈົນຮອດປີ 1700. ບັນນາທິການແລະຜູ້ປະກອບສ່ວນຂອງພາກສ່ວນ ໃໝ່ ປະກອບມີ John Dee, John Mellis, Robert Hartwell, Thomas Willsford, ແລະສຸດທ້າຍ Edward Hatton.
ລໍາດັບເລຂາຄະນິດຂອງ Arithmetico: ໃນຄະນິດສາດ, ລໍາດັບເລຂາຄະນິດສາດ ເປັນຜົນມາຈາກການຄູນໄລຍະໄລຍະຂອງຄວາມຄືບ ໜ້າ ເລຂາຄະນິດທີ່ມີເງື່ອນໄຂທີ່ສອດຄ້ອງກັນຂອງຄວາມຄືບຫນ້າເລກຄະນິດສາດ. ເຮັດໃຫ້ຫຼາຍຢ່າງຊັດເຈນ, ໄດ້ n th ໄລຍະຂອງລໍາດັບ arithmetico, ເລຂາຄະນິດແມ່ນຜະລິດຕະພັນຂອງ n ໄລຍະຂອງ sequenceand ການກ່ຽວກັບເລກ n ໄລຍະຂອງເລຂາຄະນິດຫນຶ່ງ th ທີ. ລໍາດັບເລຂາຄະນິດຂອງ Arithmetico - ເກີດຂື້ນໃນການ ນຳ ໃຊ້ຕ່າງໆ, ເຊັ່ນວ່າການ ຄຳ ນວນຄ່າທີ່ຄາດໄວ້ໃນທິດສະດີຄວາມເປັນໄປໄດ້. ຍົກຕົວຢ່າງ, ລຳ ດັບ
ລໍາດັບເລຂາຄະນິດຂອງ Arithmetico: ໃນຄະນິດສາດ, ລໍາດັບເລຂາຄະນິດສາດ ເປັນຜົນມາຈາກການຄູນໄລຍະໄລຍະຂອງຄວາມຄືບ ໜ້າ ເລຂາຄະນິດທີ່ມີເງື່ອນໄຂທີ່ສອດຄ້ອງກັນຂອງຄວາມຄືບຫນ້າເລກຄະນິດສາດ. ເຮັດໃຫ້ຫຼາຍຢ່າງຊັດເຈນ, ໄດ້ n th ໄລຍະຂອງລໍາດັບ arithmetico, ເລຂາຄະນິດແມ່ນຜະລິດຕະພັນຂອງ n ໄລຍະຂອງ sequenceand ການກ່ຽວກັບເລກ n ໄລຍະຂອງເລຂາຄະນິດຫນຶ່ງ th ທີ. ລໍາດັບເລຂາຄະນິດຂອງ Arithmetico - ເກີດຂື້ນໃນການ ນຳ ໃຊ້ຕ່າງໆ, ເຊັ່ນວ່າການ ຄຳ ນວນຄ່າທີ່ຄາດໄວ້ໃນທິດສະດີຄວາມເປັນໄປໄດ້. ຍົກຕົວຢ່າງ, ລຳ ດັບ
ລໍາດັບເລຂາຄະນິດຂອງ Arithmetico: ໃນຄະນິດສາດ, ລໍາດັບເລຂາຄະນິດສາດ ເປັນຜົນມາຈາກການຄູນໄລຍະໄລຍະຂອງຄວາມຄືບ ໜ້າ ເລຂາຄະນິດທີ່ມີເງື່ອນໄຂທີ່ສອດຄ້ອງກັນຂອງຄວາມຄືບຫນ້າເລກຄະນິດສາດ. ເຮັດໃຫ້ຫຼາຍຢ່າງຊັດເຈນ, ໄດ້ n th ໄລຍະຂອງລໍາດັບ arithmetico, ເລຂາຄະນິດແມ່ນຜະລິດຕະພັນຂອງ n ໄລຍະຂອງ sequenceand ການກ່ຽວກັບເລກ n ໄລຍະຂອງເລຂາຄະນິດຫນຶ່ງ th ທີ. ລໍາດັບເລຂາຄະນິດຂອງ Arithmetico - ເກີດຂື້ນໃນການ ນຳ ໃຊ້ຕ່າງໆ, ເຊັ່ນວ່າການ ຄຳ ນວນຄ່າທີ່ຄາດໄວ້ໃນທິດສະດີຄວາມເປັນໄປໄດ້. ຍົກຕົວຢ່າງ, ລຳ ດັບ
ລໍາດັບເລຂາຄະນິດຂອງ Arithmetico: ໃນຄະນິດສາດ, ລໍາດັບເລຂາຄະນິດສາດ ເປັນຜົນມາຈາກການຄູນໄລຍະໄລຍະຂອງຄວາມຄືບ ໜ້າ ເລຂາຄະນິດທີ່ມີເງື່ອນໄຂທີ່ສອດຄ້ອງກັນຂອງຄວາມຄືບຫນ້າເລກຄະນິດສາດ. ເຮັດໃຫ້ຫຼາຍຢ່າງຊັດເຈນ, ໄດ້ n th ໄລຍະຂອງລໍາດັບ arithmetico, ເລຂາຄະນິດແມ່ນຜະລິດຕະພັນຂອງ n ໄລຍະຂອງ sequenceand ການກ່ຽວກັບເລກ n ໄລຍະຂອງເລຂາຄະນິດຫນຶ່ງ th ທີ. ລໍາດັບເລຂາຄະນິດຂອງ Arithmetico - ເກີດຂື້ນໃນການ ນຳ ໃຊ້ຕ່າງໆ, ເຊັ່ນວ່າການ ຄຳ ນວນຄ່າທີ່ຄາດໄວ້ໃນທິດສະດີຄວາມເປັນໄປໄດ້. ຍົກຕົວຢ່າງ, ລຳ ດັບ
ລໍາດັບເລຂາຄະນິດຂອງ Arithmetico: ໃນຄະນິດສາດ, ລໍາດັບເລຂາຄະນິດສາດ ເປັນຜົນມາຈາກການຄູນໄລຍະໄລຍະຂອງຄວາມຄືບ ໜ້າ ເລຂາຄະນິດທີ່ມີເງື່ອນໄຂທີ່ສອດຄ້ອງກັນຂອງຄວາມຄືບຫນ້າເລກຄະນິດສາດ. ເຮັດໃຫ້ຫຼາຍຢ່າງຊັດເຈນ, ໄດ້ n th ໄລຍະຂອງລໍາດັບ arithmetico, ເລຂາຄະນິດແມ່ນຜະລິດຕະພັນຂອງ n ໄລຍະຂອງ sequenceand ການກ່ຽວກັບເລກ n ໄລຍະຂອງເລຂາຄະນິດຫນຶ່ງ th ທີ. ລໍາດັບເລຂາຄະນິດຂອງ Arithmetico - ເກີດຂື້ນໃນການ ນຳ ໃຊ້ຕ່າງໆ, ເຊັ່ນວ່າການ ຄຳ ນວນຄ່າທີ່ຄາດໄວ້ໃນທິດສະດີຄວາມເປັນໄປໄດ້. ຍົກຕົວຢ່າງ, ລຳ ດັບ
ລໍາດັບເລຂາຄະນິດຂອງ Arithmetico: ໃນຄະນິດສາດ, ລໍາດັບເລຂາຄະນິດສາດ ເປັນຜົນມາຈາກການຄູນໄລຍະໄລຍະຂອງຄວາມຄືບ ໜ້າ ເລຂາຄະນິດທີ່ມີເງື່ອນໄຂທີ່ສອດຄ້ອງກັນຂອງຄວາມຄືບຫນ້າເລກຄະນິດສາດ. ເຮັດໃຫ້ຫຼາຍຢ່າງຊັດເຈນ, ໄດ້ n th ໄລຍະຂອງລໍາດັບ arithmetico, ເລຂາຄະນິດແມ່ນຜະລິດຕະພັນຂອງ n ໄລຍະຂອງ sequenceand ການກ່ຽວກັບເລກ n ໄລຍະຂອງເລຂາຄະນິດຫນຶ່ງ th ທີ. ລໍາດັບເລຂາຄະນິດຂອງ Arithmetico - ເກີດຂື້ນໃນການ ນຳ ໃຊ້ຕ່າງໆ, ເຊັ່ນວ່າການ ຄຳ ນວນຄ່າທີ່ຄາດໄວ້ໃນທິດສະດີຄວາມເປັນໄປໄດ້. ຍົກຕົວຢ່າງ, ລຳ ດັບ
ເລກຄະນິດສາດ: Arithmetic ແມ່ນສາຂາຂອງຄະນິດສາດເຊິ່ງປະກອບດ້ວຍການສຶກສາຕົວເລກ, ໂດຍສະເພາະກ່ຽວກັບຄຸນລັກສະນະຂອງການ ດຳ ເນີນງານຕາມປະເພນີທີ່ມີຕໍ່ພວກມັນ - ເພີ່ມ, ການຫັກລົບ, ຄູນ, ການແບ່ງ, ການອອກ ກຳ ລັງກາຍແລະການສະກັດຮາກ. ຄະນິດສາດແມ່ນສ່ວນ ໜຶ່ງ ຂອງທິດສະດີ, ແລະທິດສະດີເລກໄດ້ຖືກພິຈາລະນາວ່າເປັນ ໜຶ່ງ ໃນການແບ່ງຂັ້ນເທິງຂອງຄະນິດສາດທີ່ທັນສະ ໄໝ, ພ້ອມດ້ວຍຄະນິດສາດ, ເລຂາຄະນິດແລະການວິເຄາະ. ຄຳ ສັບກ່ຽວກັບ ເລກຄະນິດສາດ ແລະ ເລກຄະນິດສາດ ສູງ ໄດ້ຖືກ ນຳ ໃຊ້ຈົນຮອດຕົ້ນສະຕະວັດທີ 20 ເປັນສັບຄ້າຍຄືກັນ ສຳ ລັບ ທິດສະດີເລກ , ແລະບາງຄັ້ງກໍ່ຍັງໃຊ້ເພື່ອອ້າງອີງເຖິງສ່ວນ ໜຶ່ງ ທີ່ກວ້າງຂວາງຂອງທິດສະດີເລກ.
ເລກຄະນິດສາດ - ເລຂາຄະນິດ: ໃນຄະນິດສາດ, ເລກຄະນິດສາດ – ເລຂາຄະນິດ ຂອງສອງຕົວເລກຕົວບວກ x ແລະ y ແມ່ນ ກຳ ນົດດັ່ງຕໍ່ໄປນີ້:
ຄວາມບໍ່ສະເຫມີພາບຂອງເລກຄະນິດສາດແລະເລຂາຄະນິດ: ໃນຄະນິດສາດ, ຄວາມບໍ່ສະ ເໝີ ພາບຂອງວິທີເລກຄະນິດສາດແລະເລຂາຄະນິດ , ຫຼືເວົ້າສັ້ນໆກວ່າ ຄວາມບໍ່ສະ ເໝີ ພາບ AM – GM , ລະບຸວ່າຕົວເລກເລກຄະນິດສາດຂອງບັນຊີຂອງຕົວເລກຕົວຈິງທີ່ບໍ່ລົບແມ່ນສູງກວ່າຫຼືເທົ່າກັບຄ່າສະເລ່ຍເລຂາຄະນິດຂອງບັນຊີດຽວກັນ; ແລະໃນຕໍ່ ໜ້າ, ທັງສອງວິທີແມ່ນເທົ່າທຽມກັນຖ້າວ່າແລະທຸກໆຕົວເລກໃນບັນຊີແມ່ນເທົ່າກັນ.
ເລຂາຄະນິດ ໝາຍ ເລກ: ໃນຄະນິດສາດ, ວິຊາ ເລຂາຄະນິດ ແມ່ນຕົວເລກຫຼືສະເລ່ຍ, ເຊິ່ງສະແດງເຖິງທ່າອ່ຽງໃຈກາງຫຼືມູນຄ່າປົກກະຕິຂອງຕົວເລກທີ່ ກຳ ນົດໄວ້ໂດຍການ ນຳ ໃຊ້ຜະລິດຕະພັນຂອງຄຸນຄ່າຂອງພວກມັນ. ສະເລ່ຍຂອງເລຂາຄະນິດໄດ້ຖືກ ກຳ ນົດເປັນ ຮາກເລກທີ n ຂອງຜະລິດຕະພັນຂອງ ຈຳ ນວນ n , ເຊັ່ນ, ສຳ ລັບຊຸດຂອງຕົວເລກ x 1 , x 2 , ... , x n , ຕົວເລກເລຂາຄະນິດແມ່ນຖືກ ກຳ ນົດເປັນ
ໜ່ວຍ ງານຕາມເຫດຜົນເລກຄະນິດສາດ: ໃນການຄິດໄລ່ຄອມພິວເຕີ້, ໜ່ວຍ ງານຕາມເຫດຜົນກ່ຽວກັບເລກຄະນິດສາດ (ALU) ແມ່ນວົງຈອນດິຈິຕອນປະສົມປະສານທີ່ເຮັດ ໜ້າ ທີ່ກ່ຽວກັບເລກຄະນິດສາດແລະຂີດຕໍ່ເລກຖານສອງ. ນີ້ແມ່ນກົງກັນຂ້າມກັບ ໜ່ວຍ ລອຍນໍ້າຈຸດ (FPU), ເຊິ່ງ ດຳ ເນີນການກັບຕົວເລກຈຸດລອຍ. ມັນແມ່ນສິ່ງກໍ່ສ້າງພື້ນຖານຂອງວົງຈອນຄອມພິວເຕີ້ຫລາຍປະເພດ, ລວມທັງ ໜ່ວຍ ງານປະມວນຜົນສູນກາງ (CPU) ຂອງຄອມພິວເຕີ້, FPUs, ແລະ ໜ່ວຍ ປະມວນຜົນກາຟິກ (GPUs).
ເລກຄະນິດສາດ: Arithmetic ແມ່ນສາຂາຂອງຄະນິດສາດເຊິ່ງປະກອບດ້ວຍການສຶກສາຕົວເລກ, ໂດຍສະເພາະກ່ຽວກັບຄຸນລັກສະນະຂອງການ ດຳ ເນີນງານຕາມປະເພນີທີ່ມີຕໍ່ພວກມັນ - ເພີ່ມ, ການຫັກລົບ, ຄູນ, ການແບ່ງ, ການອອກ ກຳ ລັງກາຍແລະການສະກັດຮາກ. ຄະນິດສາດແມ່ນສ່ວນ ໜຶ່ງ ຂອງທິດສະດີ, ແລະທິດສະດີເລກໄດ້ຖືກພິຈາລະນາວ່າເປັນ ໜຶ່ງ ໃນການແບ່ງຂັ້ນເທິງຂອງຄະນິດສາດທີ່ທັນສະ ໄໝ, ພ້ອມດ້ວຍຄະນິດສາດ, ເລຂາຄະນິດແລະການວິເຄາະ. ຄຳ ສັບກ່ຽວກັບ ເລກຄະນິດສາດ ແລະ ເລກຄະນິດສາດ ສູງ ໄດ້ຖືກ ນຳ ໃຊ້ຈົນຮອດຕົ້ນສະຕະວັດທີ 20 ເປັນສັບຄ້າຍຄືກັນ ສຳ ລັບ ທິດສະດີເລກ , ແລະບາງຄັ້ງກໍ່ຍັງໃຊ້ເພື່ອອ້າງອີງເຖິງສ່ວນ ໜຶ່ງ ທີ່ກວ້າງຂວາງຂອງທິດສະດີເລກ.
ການວິເຄາະເລກຄະນິດສາດ: ການ ຄິດໄລ່ເລກຄະນິດສາດ ແມ່ນໂຄງການຄົ້ນຄ້ວາໃນພື້ນຖານຄະນິດສາດທີ່ ດຳ ເນີນໃນເຄິ່ງທີ່ສອງຂອງສະຕະວັດທີ 19.
ການວິເຄາະເລກຄະນິດສາດ: ການ ຄິດໄລ່ເລກຄະນິດສາດ ແມ່ນໂຄງການຄົ້ນຄ້ວາໃນພື້ນຖານຄະນິດສາດທີ່ ດຳ ເນີນໃນເຄິ່ງທີ່ສອງຂອງສະຕະວັດທີ 19.
ການວິເຄາະເລກຄະນິດສາດ: ການ ຄິດໄລ່ເລກຄະນິດສາດ ແມ່ນໂຄງການຄົ້ນຄ້ວາໃນພື້ນຖານຄະນິດສາດທີ່ ດຳ ເນີນໃນເຄິ່ງທີ່ສອງຂອງສະຕະວັດທີ 19.
ທິດສະດີທີ່ບໍ່ສົມບູນຂອງGödel: ທິດສະດີທີ່ບໍ່ສົມບູນຂອງGödel ແມ່ນສອງທິດສະດີຂອງເຫດຜົນທາງຄະນິດສາດທີ່ກ່ຽວຂ້ອງກັບຂໍ້ ຈຳ ກັດຂອງການພິສູດໃນທິດສະດີທາງທິດສະດີທາງທິດສະດີ. ຜົນໄດ້ຮັບເຫຼົ່ານີ້, ຈັດພີມມາໂດຍ Kurt Gödelໃນປີ 1931, ມີຄວາມ ສຳ ຄັນທັງທາງດ້ານຄະນິດສາດແລະໃນປັດຊະຍາຂອງຄະນິດສາດ. ທິດສະດີແມ່ນມີຢ່າງກວ້າງຂວາງ, ແຕ່ບໍ່ມີການຕີລາຄາໃນທົ່ວໂລກ, ສະແດງໃຫ້ເຫັນວ່າການສະແດງໃຫ້ເຫັນວ່າໂປແກຼມ Hilbert ໃນການຊອກຫາທິດສະດີທີ່ຕັ້ງຄົບຖ້ວນແລະສອດຄ່ອງ ສຳ ລັບຄະນິດສາດທັງ ໝົດ ແມ່ນເປັນໄປບໍ່ໄດ້.
Arithmeum: Arithmeum ແມ່ນພິພິທະພັນຄະນິດສາດທີ່ເປັນເຈົ້າຂອງໂດຍ Forschungsinstitut für Diskrete Mathematik ທີ່ມະຫາວິທະຍາໄລບອນ.
Arithmologia: Arithmologia, sive De Abditis Numerorum Mysteriis ແມ່ນວຽກ 1665 ໂດຍນັກວິຊາການ Jesuit Athanasius Kircher. ມັນຖືກຈັດພິມໂດຍ Varese, ໂຮງພິມ ສຳ ຄັນ ສຳ ລັບ ຄຳ ສັ່ງ Jesuit ໃນ Rome ໃນກາງສະຕະວັດທີ 17. ມັນໄດ້ຖືກອຸທິດໃຫ້ Franz III. Nádasdy, ຜູ້ທີ່ປ່ຽນໃຈເຫລື້ອມໃສຕໍ່ສາສະ ໜາ ກາໂຕລິກຜູ້ທີ່ທ່ານ Kircher ເຄີຍຮ່ວມອຸທິດຕົນ Oedipus Aegyptiacus . Arithmologia ແມ່ນ ໜຶ່ງ ໃນບັນດາຜົນງານຂອງ Kircher ທີ່ອຸທິດໃຫ້ແກ່ທຸກດ້ານທີ່ແຕກຕ່າງກັນຂອງສັນຍາລັກຂອງຕົວເລກ.
ຕົວເລກ: Numerology ແມ່ນຄວາມເຊື່ອໃນຄວາມ ສຳ ພັນອັນສູງສົ່ງຫຼືຄວາມລຶກລັບລະຫວ່າງ ຈຳ ນວນ ໜຶ່ງ ແລະເຫດການ ໜຶ່ງ ທີ່ກົງກັນ. ມັນກໍ່ແມ່ນການສຶກສາກ່ຽວກັບຄຸນຄ່າຕົວເລກຂອງຕົວອັກສອນໃນ ຄຳ ສັບ, ຊື່ແລະແນວຄິດ. ມັນມັກຈະກ່ຽວຂ້ອງກັບເລື່ອງແປກປະຫລາດ, ຄຽງຄູ່ກັບໂຫລະສາດແລະຄ້າຍຄືກັບສິລະປະສະຫວັນ.
Rithmomachy: Rithmomachy ແມ່ນເກມຄະນິດສາດຄະນິດສາດໃນສະຫະພາບເອີຣົບທີ່ມີຄວາມສັບສົນສູງ. ລາຍລະອຽດທີ່ຮູ້ຈັກກັນດີທີ່ສຸດໃນຄັ້ງ ທຳ ອິດແມ່ນມາຈາກສະຕະວັດທີສິບເອັດ. ການແປຕົວຈິງຂອງຊື່ແມ່ນ "ການຕໍ່ສູ້ຂອງຕົວເລກ". ເກມແມ່ນຄ້າຍຄື ໝາກ ຮຸກ, ຍົກເວັ້ນວິທີການຈັບທີ່ສຸດແມ່ນຂື້ນກັບຕົວເລກທີ່ຂຽນໄວ້ໃນແຕ່ລະສິ້ນ.
Arithmancy: ໃນ ຄຳ ສັບຕົວເລກທັນສະ ໄໝ, ເລກຄະ ນິດສາດ ແມ່ນຮູບແບບຂອງການແບ່ງປັນໂດຍອີງໃສ່ການມອບຄ່າຕົວເລກໃຫ້ແກ່ ຄຳ ສັບຫລືປະໂຫຍກ, ໂດຍວິທີການແປແບບງ່າຍໆຂອງພາສາກະເຣັກບູຮານຫລື ຄຳ ສັບພາສາເຮັບເຣີ / Aramaic, ເປັນການດັດປັບກັບຕົວ ໜັງ ສືລາຕິນ. Arithmancy ແມ່ນກ່ຽວຂ້ອງກັບຊາວຄັນເດ, Platonists, Pythagoreans, ແລະ Kabbalah. ເມື່ອການ ນຳ ໃຊ້ເລກຄະນິດສາດ ນຳ ໃຊ້ກັບຊື່ຂອງຄົນເຮົາ, ມັນແມ່ນຮູບແບບຂອງການບໍ່ ທຳ ມະດາ.
Arithmomania: Arithmomania ແມ່ນຄວາມຜິດປົກກະຕິທາງຈິດເຊິ່ງອາດຈະຖືກເບິ່ງວ່າເປັນການສະແດງອອກຂອງຄວາມຜິດປົກກະຕິທີ່ບໍ່ຄວນຄິດ (OCD). ບຸກຄົນທີ່ປະສົບກັບຄວາມຜິດປົກກະຕິນີ້ມີຄວາມຕ້ອງການທີ່ຈະນັບການກະ ທຳ ຫຼືວັດຖຸສິ່ງຂອງຕ່າງໆທີ່ຢູ່ອ້ອມຕົວເຂົາເຈົ້າ.
Arithmomania: Arithmomania ແມ່ນຄວາມຜິດປົກກະຕິທາງຈິດເຊິ່ງອາດຈະຖືກເບິ່ງວ່າເປັນການສະແດງອອກຂອງຄວາມຜິດປົກກະຕິທີ່ບໍ່ຄວນຄິດ (OCD). ບຸກຄົນທີ່ປະສົບກັບຄວາມຜິດປົກກະຕິນີ້ມີຄວາມຕ້ອງການທີ່ຈະນັບການກະ ທຳ ຫຼືວັດຖຸສິ່ງຂອງຕ່າງໆທີ່ຢູ່ອ້ອມຕົວເຂົາເຈົ້າ.
Arithmometer: Arithmometer ຫຼື Arithmomètre ແມ່ນເຄື່ອງຄິດໄລ່ກົນຈັກດິຈິຕອນ ທຳ ອິດທີ່ມີຄວາມເຂັ້ມແຂງແລະເຊື່ອຖືໄດ້ພຽງພໍທີ່ຈະ ນຳ ໃຊ້ປະ ຈຳ ວັນໃນສະພາບແວດລ້ອມຂອງຫ້ອງການ. ເຄື່ອງຄິດໄລ່ນີ້ສາມາດເພີ່ມແລະຫັກສອງຕົວເລກໄດ້ໂດຍກົງແລະສາມາດປະຕິບັດການຄູນແລະການແບ່ງຂັ້ນຍາວໄດ້ຢ່າງມີປະສິດຕິຜົນໂດຍການ ນຳ ໃຊ້ເຄື່ອງສະສົມເພື່ອຍ້າຍຜົນໄດ້ຮັບ.
Arithmometer: Arithmometer ຫຼື Arithmomètre ແມ່ນເຄື່ອງຄິດໄລ່ກົນຈັກດິຈິຕອນ ທຳ ອິດທີ່ມີຄວາມເຂັ້ມແຂງແລະເຊື່ອຖືໄດ້ພຽງພໍທີ່ຈະ ນຳ ໃຊ້ປະ ຈຳ ວັນໃນສະພາບແວດລ້ອມຂອງຫ້ອງການ. ເຄື່ອງຄິດໄລ່ນີ້ສາມາດເພີ່ມແລະຫັກສອງຕົວເລກໄດ້ໂດຍກົງແລະສາມາດປະຕິບັດການຄູນແລະການແບ່ງຂັ້ນຍາວໄດ້ຢ່າງມີປະສິດຕິຜົນໂດຍການ ນຳ ໃຊ້ເຄື່ອງສະສົມເພື່ອຍ້າຍຜົນໄດ້ຮັບ.
Arithmometer: Arithmometer ຫຼື Arithmomètre ແມ່ນເຄື່ອງຄິດໄລ່ກົນຈັກດິຈິຕອນ ທຳ ອິດທີ່ມີຄວາມເຂັ້ມແຂງແລະເຊື່ອຖືໄດ້ພຽງພໍທີ່ຈະ ນຳ ໃຊ້ປະ ຈຳ ວັນໃນສະພາບແວດລ້ອມຂອງຫ້ອງການ. ເຄື່ອງຄິດໄລ່ນີ້ສາມາດເພີ່ມແລະຫັກສອງຕົວເລກໄດ້ໂດຍກົງແລະສາມາດປະຕິບັດການຄູນແລະການແບ່ງຂັ້ນຍາວໄດ້ຢ່າງມີປະສິດຕິຜົນໂດຍການ ນຳ ໃຊ້ເຄື່ອງສະສົມເພື່ອຍ້າຍຜົນໄດ້ຮັບ.
Numerophobia: ຄວາມກັງວົນ ກ່ຽວກັບ Numerophobia , arithmophobia ຫຼື ຄະນິດສາດ ແມ່ນຄວາມຜິດກະຕິກັງວົນໃຈ, ບ່ອນທີ່ສະພາບການມີຄວາມຢ້ານກົວທີ່ຈະຈັດການກັບຕົວເລກຫຼືຄະນິດສາດ. ບາງຄັ້ງ numerophobia ໝາຍ ເຖິງຄວາມຢ້ານກົວຕໍ່ຕົວເລກສະເພາະ.
Arithmancy: ໃນ ຄຳ ສັບຕົວເລກທັນສະ ໄໝ, ເລກຄະ ນິດສາດ ແມ່ນຮູບແບບຂອງການແບ່ງປັນໂດຍອີງໃສ່ການມອບຄ່າຕົວເລກໃຫ້ແກ່ ຄຳ ສັບຫລືປະໂຫຍກ, ໂດຍວິທີການແປແບບງ່າຍໆຂອງພາສາກະເຣັກບູຮານຫລື ຄຳ ສັບພາສາເຮັບເຣີ / Aramaic, ເປັນການດັດປັບກັບຕົວ ໜັງ ສືລາຕິນ. Arithmancy ແມ່ນກ່ຽວຂ້ອງກັບຊາວຄັນເດ, Platonists, Pythagoreans, ແລະ Kabbalah. ເມື່ອການ ນຳ ໃຊ້ເລກຄະນິດສາດ ນຳ ໃຊ້ກັບຊື່ຂອງຄົນເຮົາ, ມັນແມ່ນຮູບແບບຂອງການບໍ່ ທຳ ມະດາ.
Wars ຂອງແສງແລະເງົາ: The Wars of Light and Shadow ແມ່ນຊຸດຂອງປື້ມຈິນຕະນາການໂດຍ Janny Wurts. ເມື່ອສ້າງ ສຳ ເລັດແລ້ວ, ມັນຈະປະກອບມີ 5 ຫົວເລື່ອງ, ສ່ວນ 4 ຕົວ ທຳ ອິດ ສຳ ເລັດ.
Wars ຂອງແສງແລະເງົາ: The Wars of Light and Shadow ແມ່ນຊຸດຂອງປື້ມຈິນຕະນາການໂດຍ Janny Wurts. ເມື່ອສ້າງ ສຳ ເລັດແລ້ວ, ມັນຈະປະກອບມີ 5 ຫົວເລື່ອງ, ສ່ວນ 4 ຕົວ ທຳ ອິດ ສຳ ເລັດ.
Wars ຂອງແສງແລະເງົາ: The Wars of Light and Shadow ແມ່ນຊຸດຂອງປື້ມຈິນຕະນາການໂດຍ Janny Wurts. ເມື່ອສ້າງ ສຳ ເລັດແລ້ວ, ມັນຈະປະກອບມີ 5 ຫົວເລື່ອງ, ສ່ວນ 4 ຕົວ ທຳ ອິດ ສຳ ເລັດ.
ເຂດ Tana River: Tana River County ແມ່ນຄາວຕີ້ ໜຶ່ງ ໃນອະດີດແຂວງ Coast ຂອງປະເທດ Kenya. ມັນຖືກຕັ້ງຊື່ຕາມແມ່ນ້ ຳ Tana. ມີເນື້ອທີ່ 38,437 ກິໂລຕາແມັດ (14,841 ຕາລາງໄມ) ແລະມີປະຊາກອນ 315,943 ຄົນ. ນະຄອນຫຼວງແລະຕົວເມືອງທີ່ໃຫຍ່ທີ່ສຸດແມ່ນ Hola.
Arity: Arity ແມ່ນ ຈຳ ນວນຂອງການໂຕ້ຖຽງຫຼືການປະຕິບັດງານທີ່ປະຕິບັດໂດຍ ໜ້າ ທີ່ຫຼືການ ດຳ ເນີນງານຕາມເຫດຜົນ, ຄະນິດສາດແລະວິທະຍາສາດຄອມພິວເຕີ. ໃນທາງຄະນິດສາດ, ຄວາມສົງໄສອາດຈະຖືກຕັ້ງຊື່ໃຫ້ເປັນ ອັນດັບ , ແຕ່ ຄຳ ສັບນີ້ສາມາດມີຄວາມ ໝາຍ ອື່ນອີກໃນຄະນິດສາດ ໃນເຫດຜົນແລະປັດຊະຍາ, ມັນຍັງຖືກເອີ້ນວ່າ adicity ແລະ ລະດັບ . ໃນພາສາ, ປົກກະຕິແລ້ວມັນແມ່ນຊື່ valency .
ເຄືອຂ່າຍ neural ທຽມ: ເຄືອຂ່າຍ neural ທຽມ ( ANNs ), ໂດຍປົກກະຕິເອີ້ນວ່າ ເຄືອຂ່າຍ neural ( NNs ), ແມ່ນລະບົບຄອມພິວເຕີ້ທີ່ໄດ້ຮັບແຮງບັນດານໃຈຈາກເຄືອຂ່າຍທາງຊີວະພາບທາງຊີວະພາບທີ່ປະກອບເປັນສະ ໝອງ ຂອງສັດ.
Artemis: Artemis ແມ່ນເທບທິດາຂອງກະເຣັກຂອງການລ່າສັດ, ຖິ່ນແຫ້ງແລ້ງ, ສັດປ່າ, ດວງຈັນ, ແລະພົມມະຈັນ. ເທບທິດາ Diana ແມ່ນທຽບເທົ່າກັບນາງ Roman.
Arintica: Arintica ແມ່ນ stratovolcano ຕັ້ງຢູ່ໃນພາກພື້ນ Arica y Parinacota ຂອງປະເທດຊິລີ, ໃກ້ກັບຊາຍແດນໂບລີເວຍ. ມັນຕັ້ງຢູ່ທາງທິດ ເໜືອ ຂອງ Salar de Surire. ພູເຂົາໄຟມີກອງປະຊຸມໃຫຍ່ຢູ່ພາກ ເໜືອ, ການປະຊຸມພາກໃຕ້ທີ່ສັ້ນກວ່າເລັກນ້ອຍແລະຈຸດສູງສຸດຂອງບໍລິສັດຍ່ອຍຢູ່ທາງທິດຕາເວັນຕົກ. ຮ່ອມພູນ້ ຳ ກ້ອນແມ່ນຢູ່ລະຫວ່າງກອງປະຊຸມສຸດຍອດ. ລະດັບຄວາມສູງຂອງຫິມະແມ່ນ 5,590 ແມັດ (18,340 ຟຸດ). ສິນລະປະຂັ້ນຕອນ II ທີ່ພົບເຫັນຢູ່ Arintica ມີຄວາມສູງຈາກ 4,350 ແມັດ (14,270 ຟຸດ) ທາງດ້ານໃຕ້ຂອງທາງພາກ ເໜືອ ເຖິງ 4,550 ແມັດ (14,930 ຟຸດ) ທາງດ້ານຕາເວັນອອກ. ທາງຝັ່ງທິດຕາເວັນຕົກເຂົາເຈົ້າມີຄວາມສູງ 4,400 ແມັດ (14,400 ຟຸດ). ໃນ ຈຳ ນວນທັງ ໝົດ, ມີ 5 ໜ່ວຍ ໃຫຍ່ໄດ້ອ້ອມຮອບ Arintica ແລະກໍ່ນ້ ຳ ເຂົ້າໄປໃນ Salar de Surire. ປະຈຸບັນ, ຫີນກ້ອນຫີນພວມເຄື່ອນໄຫວຢູ່ເທິງພູ.
ພາສາ Arritinngithigh: Aritinngithigh ແມ່ນພາສາດັ້ງເດີມຂອງອົດສະຕາລີທີ່ເຄີຍເວົ້າໃນ Cape York ໃນລັດ Queensland.
ພາສາ Arritinngithigh: Aritinngithigh ແມ່ນພາສາດັ້ງເດີມຂອງອົດສະຕາລີທີ່ເຄີຍເວົ້າໃນ Cape York ໃນລັດ Queensland.
ພາສາ Arritinngithigh: Aritinngithigh ແມ່ນພາສາດັ້ງເດີມຂອງອົດສະຕາລີທີ່ເຄີຍເວົ້າໃນ Cape York ໃນລັດ Queensland.
ພາສາ Arritinngithigh: Aritinngithigh ແມ່ນພາສາດັ້ງເດີມຂອງອົດສະຕາລີທີ່ເຄີຍເວົ້າໃນ Cape York ໃນລັດ Queensland.
Ramil Aritkulov: Ramil Kamilevich Aritkulov ແມ່ນນັກແລ່ນໄລຍະກາງຊາວລັດເຊຍຜູ້ຊ່ຽວຊານດ້ານຄວາມສູງ 800 ແມັດ.
ບໍລິສັດ SK Aritma Prague: SK Aritma Prague ແມ່ນສະໂມສອນບານເຕະຊາວເຊັກຕັ້ງຢູ່ Prague-Vokovice. ປະຈຸບັນມັນຫລິ້ນໃນພະແນກສີ່ຂອງເຊັກ.
ບໍລິສັດ SK Aritma Prague: SK Aritma Prague ແມ່ນສະໂມສອນບານເຕະຊາວເຊັກຕັ້ງຢູ່ Prague-Vokovice. ປະຈຸບັນມັນຫລິ້ນໃນພະແນກສີ່ຂອງເຊັກ.
ເລກຄະນິດສາດ: Arithmetic ແມ່ນສາຂາຂອງຄະນິດສາດເຊິ່ງປະກອບດ້ວຍການສຶກສາຕົວເລກ, ໂດຍສະເພາະກ່ຽວກັບຄຸນລັກສະນະຂອງການ ດຳ ເນີນງານຕາມປະເພນີທີ່ມີຕໍ່ພວກມັນ - ເພີ່ມ, ການຫັກລົບ, ຄູນ, ການແບ່ງ, ການອອກ ກຳ ລັງກາຍແລະການສະກັດຮາກ. ຄະນິດສາດແມ່ນສ່ວນ ໜຶ່ງ ຂອງທິດສະດີ, ແລະທິດສະດີເລກໄດ້ຖືກພິຈາລະນາວ່າເປັນ ໜຶ່ງ ໃນການແບ່ງຂັ້ນເທິງຂອງຄະນິດສາດທີ່ທັນສະ ໄໝ, ພ້ອມດ້ວຍຄະນິດສາດ, ເລຂາຄະນິດແລະການວິເຄາະ. ຄຳ ສັບກ່ຽວກັບ ເລກຄະນິດສາດ ແລະ ເລກຄະນິດສາດ ສູງ ໄດ້ຖືກ ນຳ ໃຊ້ຈົນຮອດຕົ້ນສະຕະວັດທີ 20 ເປັນສັບຄ້າຍຄືກັນ ສຳ ລັບ ທິດສະດີເລກ , ແລະບາງຄັ້ງກໍ່ຍັງໃຊ້ເພື່ອອ້າງອີງເຖິງສ່ວນ ໜຶ່ງ ທີ່ກວ້າງຂວາງຂອງທິດສະດີເລກ.
Aritmija: Aritmija ອາດຈະອ້າງເຖິງ: Aritmija (ນະວະນິຍາຍ) , ນະວະນິຍາຍປີ 2004 ໂດຍນັກຂຽນຊາວສະໂລເວເນຍ Jani Virk Aritmija (ອັລບັມ) , ປີ 2006 ອັລບັມໂດຍວົງດົນຕີ Croatian Vatra
Aritmija: Aritmija ອາດຈະອ້າງເຖິງ: Aritmija (ນະວະນິຍາຍ) , ນະວະນິຍາຍປີ 2004 ໂດຍນັກຂຽນຊາວສະໂລເວເນຍ Jani Virk Aritmija (ອັລບັມ) , ປີ 2006 ອັລບັມໂດຍວົງດົນຕີ Croatian Vatra
Aritmija (ນະວະນິຍາຍ): Aritmija ແມ່ນນະວະນິຍາຍຂອງນັກຂຽນ Slovenia Jani Virk. ມັນໄດ້ຖືກຈັດພີມມາຄັ້ງທໍາອິດໃນປີ 2004.
Michiyo Arito: Michiyo Arito ເປັນນັກກິລາເບດບານມືອາຊີບຄົນທີສາມຂອງຍີ່ປຸ່ນໃນ Nippon Baseball ມືອາຊີບ. ລາວໄດ້ຫຼີ້ນອາຊີບທັງ ໝົດ ຂອງລາວ ສຳ ລັບ Lotte Orions ຕັ້ງແຕ່ປີ 1969 ເຖິງປີ 1986. ລາວເປັນ Pacific Rookie of the Year ໃນປີ 1969.
ສະຖານີ Arito: ສະຖານີ Arito ແມ່ນສະຖານີລົດໄຟໃນເມືອງ Noheji, ເມືອງ Kamikita, ແຂວງ Aomori, ປະເທດຍີ່ປຸ່ນ, ດຳ ເນີນງານໂດຍບໍລິສັດທາງລົດໄຟ East Japan.
Aritomo: Aritomo ແມ່ນຊື່ຊາຍຍີ່ປຸ່ນທີ່ມີຊື່ຊາຍ. ບຸກຄົນທີ່ມີຊື່ສຽງປະກອບມີ: Aritomo Gotō , ພົນເຮືອເອກ Imperial Japanese Navy Yamagata Aritomo , ພົນເອກແລະນາຍົກລັດຖະມົນຕີຍີ່ປຸ່ນ
Aritomo Gotō: Aritomo Gotō ເປັນນາຍພົນເຮືອເອກໃນກອງທັບເຮືອຍີ່ປຸ່ນໃນສະ ໄໝ ສົງຄາມໂລກຄັ້ງທີ 2.
Aritomo Gotō: Aritomo Gotō ເປັນນາຍພົນເຮືອເອກໃນກອງທັບເຮືອຍີ່ປຸ່ນໃນສະ ໄໝ ສົງຄາມໂລກຄັ້ງທີ 2.
Yamagata Aritomo: Gensui Prince Yamagata Aritomo , ທີ່ເອີ້ນກັນວ່າ Prince Yamagata Kyōsuke , ແມ່ນຜູ້ບັນຊາການທະຫານຊັ້ນສູງຂອງຍີ່ປຸ່ນ, ໄດ້ຖືກເລືອກຕັ້ງເປັນນາຍົກລັດຖະມົນຕີຍີ່ປຸ່ນສອງຄັ້ງ, ແລະເປັນສະມາຊິກຊັ້ນ ນຳ ຂອງ genrō , ເຊິ່ງເປັນກຸ່ມຂອງລັດຊັ້ນສູງທີ່ປົກຄອງປະເທດຍີ່ປຸ່ນຫຼັງຈາກການຟື້ນຟູ Meiji. ໃນຖານະທີ່ເປັນຫົວ ໜ້າ ກອງບັນຊາການກອງທັບຍີ່ປຸ່ນ Imperial, ທ່ານໄດ້ເປັນຫົວ ໜ້າ ສະຖາປະນິກແຫ່ງອານາຈັກທະຫານຂອງຍີ່ປຸ່ນແລະອຸດົມການປະຕິກິລິຍາ. ດ້ວຍເຫດຜົນນີ້, ນັກປະຫວັດສາດບາງຄົນຖືວ່າຢາມາກາຕາເປັນ "ພໍ່" ຂອງການທະຫານຍີ່ປຸ່ນ.
Ariton, Alabama: Ariton ແມ່ນຕົວເມືອງ ໜຶ່ງ ໃນ Dale County, Alabama, ສະຫະລັດອາເມລິກາ. ໃນການສໍາຫລວດ 2010 ປະຊາກອນແມ່ນ 764. ມັນໄດ້ຖືກລວມເຂົ້າໃນເດືອນເມສາ 1906 ຊື່ເປັນ blend ຂອງຊື່ເມືອງສອງບັນພະບຸລຸດຂອງຕົນ: Ari osto ແລະ Charl ໂຕນ.
Ariton, Alabama: Ariton ແມ່ນຕົວເມືອງ ໜຶ່ງ ໃນ Dale County, Alabama, ສະຫະລັດອາເມລິກາ. ໃນການສໍາຫລວດ 2010 ປະຊາກອນແມ່ນ 764. ມັນໄດ້ຖືກລວມເຂົ້າໃນເດືອນເມສາ 1906 ຊື່ເປັນ blend ຂອງຊື່ເມືອງສອງບັນພະບຸລຸດຂອງຕົນ: Ari osto ແລະ Charl ໂຕນ.
Ariton, Alabama: Ariton ແມ່ນຕົວເມືອງ ໜຶ່ງ ໃນ Dale County, Alabama, ສະຫະລັດອາເມລິກາ. ໃນການສໍາຫລວດ 2010 ປະຊາກອນແມ່ນ 764. ມັນໄດ້ຖືກລວມເຂົ້າໃນເດືອນເມສາ 1906 ຊື່ເປັນ blend ຂອງຊື່ເມືອງສອງບັນພະບຸລຸດຂອງຕົນ: Ari osto ແລະ Charl ໂຕນ.
Ariton, Alabama: Ariton ແມ່ນຕົວເມືອງ ໜຶ່ງ ໃນ Dale County, Alabama, ສະຫະລັດອາເມລິກາ. ໃນການສໍາຫລວດ 2010 ປະຊາກອນແມ່ນ 764. ມັນໄດ້ຖືກລວມເຂົ້າໃນເດືອນເມສາ 1906 ຊື່ເປັນ blend ຂອງຊື່ເມືອງສອງບັນພະບຸລຸດຂອງຕົນ: Ari osto ແລະ Charl ໂຕນ.
Aritox: Aritox ໃນໄລຍະເກີດຂື້ນໃນຊື່ຂອງພູມຕ້ານທານ monoclonal ແລະຊີ້ໃຫ້ເຫັນວ່າພວກມັນເຊື່ອມໂຍງກັບລະບົບຕ່ອງໂສ້ຂອງທາດໂປຼຕີນທາດ ricin. Telimomab aritox Zolimomab aritox
Zolimomab aritox: Zolimomab aritox ແມ່ນສານຕ້ານອະນຸມູນອິດສະລະ monoclonal ທີ່ໄດ້ຮັບການສືບສວນກ່ຽວກັບການຮັກສາລະບົບ lupus erythematosus ທີ່ເປັນລະບົບແລະພະຍາດຕິດຕາມ, ແຕ່ການສຶກສາບໍ່ໄດ້ສະແດງໃຫ້ເຫັນຜົນກະທົບໃນທາງບວກຂອງຢາ.
Aritra: Aritra ແມ່ນຊື່ທີ່ມີຊື່ຊາຍຂອງອິນເດຍ. ບຸກຄົນທີ່ມີຊື່ສຽງປະກອບມີ: Aritra Dutta Banik, ນັກສະແດງຮູບເງົາ Bengali Aritra Dutta, ຄ່າຍງົວຊາວສິງກະໂປ
ຮູບຖ່າຍແບບເຄື່ອນໄຫວແບບອັດຕະໂນມັດ: Assorted Motion Pictures ແມ່ນເຮືອນຜະລິດທີ່ຕັ້ງຢູ່ເມືອງ Mumbai, ປະເທດອິນເດຍ. ເຮືອນໄດ້ຖືກສ້າງຕັ້ງຂຶ້ນໂດຍ Aritra Das, Sarbani Mukherjee ແລະ Ram Kamal Mukherjee ໃນປີ 27 ສິງຫາ 2015.
Aritra Dutta: Aritra Dutta ແມ່ນນັກກະ ແລັມ ຊາວສິງກະໂປ. ໃນເດືອນຕຸລາ 2018, ລາວໄດ້ຖືກຕັ້ງຊື່ໃຫ້ເປັນທີມໃນປະເທດສິງກະໂປ ສຳ ລັບການແຂ່ງຂັນເຕະບານຊີງແຊັມໂລກ ICC World Division 2018 ທີ່ສາມໃນປະເທດໂອມານ. ລາວໄດ້ຫລິ້ນໃນການແຂ່ງຂັນນັດເປີດສະ ໜາມ ຂອງສິງກະໂປ, ຕໍ່ຕ້ານໂອມານໃນວັນທີ 10 ພະຈິກ 2018, ລາວເປັນຜູ້ ນຳ ທີ່ໄດ້ຄະແນນ ນຳ ໜ້າ ສຳ ລັບປະເທດສິງກະໂປໃນການແຂ່ງຂັນ, ໂດຍ 204 ແຂ່ງໃນ 5 ນັດ.
Banik Aritra Dutta: Aritra Dutta Banik ແມ່ນນັກສະແດງຮູບເງົາຊາວເບັງກາລີເຊິ່ງໄດ້ສະແດງ ໜ້າ ຈໍຫຼາຍຄັ້ງຕັ້ງແຕ່ປີ 2003. ລາວໄດ້ສະແດງເປັນຄັ້ງ ທຳ ອິດໃນພາສາ Bengali megaserial Tithir Atithi , ເຊິ່ງໄດ້ອອກອາກາດທາງໂທລະພາບ ETV Bangla ແຕ່ປີ 2003 ເຖິງປີ 2009. ການສະແດງຄວາມເປັນຈິງຂອງການເຕັ້ນຂອງ Mithun Chakraborty, Dance Bangla Dance Junior (2007), ໃນນັ້ນ, ລາວໄດ້ສະແດງການສະແດງພ້ອມດ້ວຍ Tathoi Deb. ຕັ້ງແຕ່ນັ້ນມາ, ລາວໄດ້ສະແດງໃນຮູບເງົາເບັງກາລີຫຼາຍເລື່ອງ.
Aritsugu: Aritsugu ແມ່ນມີດແລະຜະລິດຕະພັນເຄື່ອງໃຊ້ ສຳ ລັບແຕ່ງຢູ່ຄົວກິນຂອງຍີ່ປຸ່ນເຊິ່ງຖືກສ້າງຕັ້ງຂຶ້ນໂດຍ Fujiwara Aritsugu ໃນປີ 1560. ມັນແມ່ນ ໜຶ່ງ ໃນບັນດາຜູ້ເຮັດເຄື່ອງຫັດຖະ ກຳ ເກົ່າແກ່ທີ່ສຸດຂອງຍີ່ປຸ່ນ.
Maki Yūkō: Maki Yūkō , ເຊິ່ງເອີ້ນກັນວ່າ Maki Aritsune , ແມ່ນນັກປີນພູຍີ່ປຸ່ນ.
Arittake no Ai de: " Arittake no Ai de " (ありったけの愛で) ແມ່ນຊຸດດຽວທີ່ອອກໂດຍ Gackt ໃນວັນທີ 26 ມັງກອນ 2005 ພາຍໃຕ້ Nippon Crown. ມັນສູງສຸດຢູ່ໃນອັນດັບທີເຈັດໃນຕາຕະລາງປະ ຈຳ ອາທິດ Oricon ແລະເປັນຕາຕະລາງເປັນເວລາເຈັດອາທິດ.
Arittake no Ai de: " Arittake no Ai de " (ありったけの愛で) ແມ່ນຊຸດດຽວທີ່ອອກໂດຍ Gackt ໃນວັນທີ 26 ມັງກອນ 2005 ພາຍໃຕ້ Nippon Crown. ມັນສູງສຸດຢູ່ໃນອັນດັບທີເຈັດໃນຕາຕະລາງປະ ຈຳ ອາທິດ Oricon ແລະເປັນຕາຕະລາງເປັນເວລາເຈັດອາທິດ.
Arittake no Ai de: " Arittake no Ai de " (ありったけの愛で) ແມ່ນຊຸດດຽວທີ່ອອກໂດຍ Gackt ໃນວັນທີ 26 ມັງກອນ 2005 ພາຍໃຕ້ Nippon Crown. ມັນສູງສຸດຢູ່ໃນອັນດັບທີເຈັດໃນຕາຕະລາງປະ ຈຳ ອາທິດ Oricon ແລະເປັນຕາຕະລາງເປັນເວລາເຈັດອາທິດ.
Arittha R Wikramanayake: Arittha R Wikramanayake ແມ່ນທະນາຍຄວາມທີ່ຊ່ຽວຊານດ້ານກົດ ໝາຍ ຂອງບໍລິສັດ, ກົດ ໝາຍ ຫຼັກຊັບແລະກົດ ໝາຍ ການຄ້າ.
Arity: Arity ແມ່ນ ຈຳ ນວນຂອງການໂຕ້ຖຽງຫຼືການປະຕິບັດງານທີ່ປະຕິບັດໂດຍ ໜ້າ ທີ່ຫຼືການ ດຳ ເນີນງານຕາມເຫດຜົນ, ຄະນິດສາດແລະວິທະຍາສາດຄອມພິວເຕີ. ໃນທາງຄະນິດສາດ, ຄວາມສົງໄສອາດຈະຖືກຕັ້ງຊື່ໃຫ້ເປັນ ອັນດັບ , ແຕ່ ຄຳ ສັບນີ້ສາມາດມີຄວາມ ໝາຍ ອື່ນອີກໃນຄະນິດສາດ ໃນເຫດຜົນແລະປັດຊະຍາ, ມັນຍັງຖືກເອີ້ນວ່າ adicity ແລະ ລະດັບ . ໃນພາສາ, ປົກກະຕິແລ້ວມັນແມ່ນຊື່ valency .