Arithmancy, Arithmomania, Arithmancy

Arithmancy: ໃນ ຄຳ ສັບຕົວເລກທັນສະ ໄໝ, ເລກຄະ ນິດສາດ ແມ່ນຮູບແບບຂອງການແບ່ງປັນໂດຍອີງໃສ່ການມອບຄ່າຕົວເລກໃຫ້ແກ່ ຄຳ ສັບຫລືປະໂຫຍກ, ໂດຍວິທີການແປແບບງ່າຍໆຂອງພາສາກະເຣັກບູຮານຫລື ຄຳ ສັບພາສາເຮັບເຣີ / Aramaic, ເປັນການດັດປັບກັບຕົວ ໜັງ ສືລາຕິນ. Arithmancy ແມ່ນກ່ຽວຂ້ອງກັບຊາວຄັນເດ, Platonists, Pythagoreans, ແລະ Kabbalah. ເມື່ອການ ນຳ ໃຊ້ເລກຄະນິດສາດ ນຳ ໃຊ້ກັບຊື່ຂອງຄົນເຮົາ, ມັນແມ່ນຮູບແບບຂອງການບໍ່ ທຳ ມະດາ.
Arithmomania: Arithmomania ແມ່ນຄວາມຜິດປົກກະຕິທາງຈິດເຊິ່ງອາດຈະຖືກເບິ່ງວ່າເປັນການສະແດງອອກຂອງຄວາມຜິດປົກກະຕິທີ່ບໍ່ຄວນຄິດ (OCD). ບຸກຄົນທີ່ປະສົບກັບຄວາມຜິດປົກກະຕິນີ້ມີຄວາມຕ້ອງການທີ່ຈະນັບການກະ ທຳ ຫຼືວັດຖຸສິ່ງແວດລ້ອມຂອງພວກເຂົາ.
Arithmancy: ໃນ ຄຳ ສັບຕົວເລກທັນສະ ໄໝ, ເລກຄະ ນິດສາດ ແມ່ນຮູບແບບຂອງການແບ່ງປັນໂດຍອີງໃສ່ການມອບຄ່າຕົວເລກໃຫ້ແກ່ ຄຳ ສັບຫລືປະໂຫຍກ, ໂດຍວິທີການແປແບບງ່າຍໆຂອງພາສາກະເຣັກບູຮານຫລື ຄຳ ສັບພາສາເຮັບເຣີ / Aramaic, ເປັນການດັດປັບກັບຕົວ ໜັງ ສືລາຕິນ. Arithmancy ແມ່ນກ່ຽວຂ້ອງກັບຊາວຄັນເດ, Platonists, Pythagoreans, ແລະ Kabbalah. ເມື່ອການ ນຳ ໃຊ້ເລກຄະນິດສາດ ນຳ ໃຊ້ກັບຊື່ຂອງຄົນເຮົາ, ມັນແມ່ນຮູບແບບຂອງການບໍ່ ທຳ ມະດາ.
ເລກຄະນິດສາດ: Arithmetic ແມ່ນສາຂາຂອງຄະນິດສາດເຊິ່ງປະກອບດ້ວຍການສຶກສາຕົວເລກ, ໂດຍສະເພາະກ່ຽວກັບຄຸນລັກສະນະຂອງການປະຕິບັດງານແບບດັ້ງເດີມຂອງພວກມັນ - ເພີ່ມ, ການຫັກລົບ, ການຄູນ, ການແບ່ງ, ການອອກ ກຳ ລັງກາຍແລະການສະກັດເອົາຮາກ. ຄະນິດສາດແມ່ນສ່ວນ ໜຶ່ງ ຂອງທິດສະດີ, ແລະທິດສະດີເລກແມ່ນຖືວ່າເປັນ ໜຶ່ງ ໃນການແບ່ງຂັ້ນເທິງຂອງຄະນິດສາດທີ່ທັນສະ ໄໝ, ພ້ອມດ້ວຍຄະນິດສາດ, ເລຂາຄະນິດແລະການວິເຄາະ. ຄຳ ສັບກ່ຽວກັບ ເລກຄະນິດສາດ ແລະ ເລກຄະນິດສາດ ສູງ ໄດ້ຖືກ ນຳ ໃຊ້ຈົນຮອດຕົ້ນສະຕະວັດທີ 20 ເປັນສັບຄ້າຍຄືກັນ ສຳ ລັບ ທິດສະດີເລກ , ແລະບາງຄັ້ງກໍ່ຍັງໃຊ້ເພື່ອອ້າງອີງເຖິງສ່ວນ ໜຶ່ງ ທີ່ກວ້າງຂວາງຂອງທິດສະດີເລກ.
ການຊື້ຂາຍແບບມີລິຂະສິດ: ການຊື້ຂາຍແບບ Algorithmic ແມ່ນວິທີການ ດຳ ເນີນການ ຄຳ ສັ່ງໂດຍ ນຳ ໃຊ້ ຄຳ ແນະ ນຳ ກ່ຽວກັບການຊື້ຂາຍທີ່ມີໂປແກຼມລ່ວງ ໜ້າ ໂດຍອັດຕະໂນມັດກວມເອົາຕົວແປຕ່າງໆເຊັ່ນ: ເວລາ, ລາຄາແລະປະລິມານ. ການຊື້ຂາຍແບບນີ້ພະຍາຍາມເລັ່ງຄວາມໄວແລະຊັບພະຍາກອນຄອມພິວເຕີ້ທີ່ກ່ຽວຂ້ອງກັບພໍ່ຄ້າມະນຸດ. ໃນສະຕະວັດທີຊາວ, ການຊື້ຂາຍແບບມີ ກຳ ໄລໄດ້ຮັບຜົນກະທົບຈາກທັງພໍ່ຄ້າຂາຍຍ່ອຍແລະສະຖາບັນ. ມັນໄດ້ຖືກນໍາໃຊ້ຢ່າງກວ້າງຂວາງໂດຍທະນາຄານການລົງທືນ, ກອງທຶນບໍານານ, ກອງທຶນເຊິ່ງກັນແລະກັນແລະກອງທຶນ hedge ເຊິ່ງອາດຈະຕ້ອງການເຜີຍແຜ່ການປະຕິບັດຄໍາສັ່ງທີ່ໃຫຍ່ກວ່າຫຼືປະຕິບັດການຄ້າທີ່ໄວເກີນໄປເພື່ອໃຫ້ພໍ່ຄ້າມະນຸດມີປະຕິກິລິຍາ. ການສຶກສາໃນປີ 2019 ໄດ້ສະແດງໃຫ້ເຫັນວ່າປະມານ 92% ຂອງການຊື້ຂາຍໃນຕະຫຼາດ Forex ແມ່ນປະຕິບັດໂດຍລະບົບການຊື້ຂາຍຫຼາຍກວ່າມະນຸດ.
ຄວາມຄືບ ໜ້າ ເລກຄະນິດສາດ: ຄວາມຄືບ ໜ້າ ກ່ຽວກັບເລກຄະນິດສາດ (AP) ຫຼື ລຳ ດັບເລກຄະນິດສາດ ແມ່ນ ລຳ ດັບຂອງຕົວເລກດັ່ງກ່າວວ່າຄວາມແຕກຕ່າງລະຫວ່າງ ຄຳ ຕໍ່ເນື່ອງແມ່ນຄົງທີ່. ຍົກຕົວຢ່າງ, ລຳ ດັບ 5, 7, 9, 11, 13, 15,. .. ແມ່ນຄວາມຄືບ ໜ້າ ເລກຄະນິດສາດທີ່ມີຄວາມແຕກຕ່າງທົ່ວໄປຂອງ 2.
ຄວາມຄືບ ໜ້າ ເລກຄະນິດສາດ: ຄວາມຄືບ ໜ້າ ກ່ຽວກັບເລກຄະນິດສາດ (AP) ຫຼື ລຳ ດັບເລກຄະນິດສາດ ແມ່ນ ລຳ ດັບຂອງຕົວເລກດັ່ງກ່າວວ່າຄວາມແຕກຕ່າງລະຫວ່າງ ຄຳ ຕໍ່ເນື່ອງແມ່ນຄົງທີ່. ຍົກຕົວຢ່າງ, ລຳ ດັບ 5, 7, 9, 11, 13, 15,. .. ແມ່ນຄວາມຄືບ ໜ້າ ເລກຄະນິດສາດທີ່ມີຄວາມແຕກຕ່າງທົ່ວໄປຂອງ 2.
Arithmaurel: The Arithmaurel ແມ່ນເຄື່ອງຄິດໄລ່ກົນຈັກທີ່ມີອິນເຕີເຟດຜູ້ໃຊ້ທີ່ມີຄວາມຕັ້ງໃຈ, ໂດຍສະເພາະແມ່ນການຄູນແລະແບ່ງຕົວເລກເພາະວ່າຜົນໄດ້ຮັບຖືກສະແດງໄວເທົ່າທີ່ຈະເປັນລະຄອນປະຕິບັດການ. ມັນໄດ້ຮັບສິດທິບັດເປັນຄັ້ງ ທຳ ອິດໃນປະເທດຝຣັ່ງໂດຍ Timoleon Maurel, ໃນປີ 1842. ມັນໄດ້ຮັບຫຼຽນ ຄຳ ໃນງານວາງສະແດງລະດັບຊາດຝຣັ່ງທີ່ປາຣີໃນປີ 1849. ແຕ່ໂຊກບໍ່ດີຄວາມສັບສົນແລະຄວາມອ່ອນແອຂອງການອອກແບບຂອງມັນເຮັດໃຫ້ມັນບໍ່ສາມາດຜະລິດໄດ້.
ເລກຄະນິດສາດ: Arithmetic ແມ່ນສາຂາຂອງຄະນິດສາດເຊິ່ງປະກອບດ້ວຍການສຶກສາຕົວເລກ, ໂດຍສະເພາະກ່ຽວກັບຄຸນລັກສະນະຂອງການປະຕິບັດງານແບບດັ້ງເດີມຂອງພວກມັນ - ເພີ່ມ, ການຫັກລົບ, ການຄູນ, ການແບ່ງ, ການອອກ ກຳ ລັງກາຍແລະການສະກັດເອົາຮາກ. ຄະນິດສາດແມ່ນສ່ວນ ໜຶ່ງ ຂອງທິດສະດີ, ແລະທິດສະດີເລກແມ່ນຖືວ່າເປັນ ໜຶ່ງ ໃນການແບ່ງຂັ້ນເທິງຂອງຄະນິດສາດທີ່ທັນສະ ໄໝ, ພ້ອມດ້ວຍຄະນິດສາດ, ເລຂາຄະນິດແລະການວິເຄາະ. ຄຳ ສັບກ່ຽວກັບ ເລກຄະນິດສາດ ແລະ ເລກຄະນິດສາດ ສູງ ໄດ້ຖືກ ນຳ ໃຊ້ຈົນຮອດຕົ້ນສະຕະວັດທີ 20 ເປັນສັບຄ້າຍຄືກັນ ສຳ ລັບ ທິດສະດີເລກ , ແລະບາງຄັ້ງກໍ່ຍັງໃຊ້ເພື່ອອ້າງອີງເຖິງສ່ວນ ໜຶ່ງ ທີ່ກວ້າງຂວາງຂອງທິດສະດີເລກ.
ເລກຄະນິດສາດ - ເລຂາຄະນິດ: ໃນຄະນິດສາດ, ເລກຄະນິດສາດ – ເລຂາຄະນິດ ຂອງສອງຕົວເລກຕົວບວກ x ແລະ y ແມ່ນ ກຳ ນົດດັ່ງຕໍ່ໄປນີ້:
ຄວາມບໍ່ສະເຫມີພາບຂອງເລກຄະນິດສາດແລະເລຂາຄະນິດ: ໃນທາງຄະນິດສາດ, ຄວາມບໍ່ສະ ເໝີ ພາບຂອງວິທີເລກຄະນິດສາດແລະເລຂາຄະນິດ , ຫຼືເວົ້າສັ້ນໆກວ່າ ຄວາມບໍ່ສະ ເໝີ ພາບ AM – GM , ລະບຸວ່າຕົວເລກເລກຄະນິດສາດຂອງບັນຊີຂອງຕົວເລກຕົວຈິງທີ່ບໍ່ລົບແມ່ນສູງກວ່າຫຼືເທົ່າກັບຄ່າເລຂາຄະນິດເລຂາຄະນິດດຽວກັນ; ແລະໃນຕໍ່ ໜ້າ, ທັງສອງວິທີແມ່ນເທົ່າທຽມກັນຖ້າວ່າແລະທຸກໆຕົວເລກໃນບັນຊີແມ່ນເທົ່າກັນ.
ເລກຄະນິດສາດ - ເລຂາຄະນິດ: ໃນຄະນິດສາດ, ເລກຄະນິດສາດ – ເລຂາຄະນິດ ຂອງສອງຕົວເລກຕົວບວກ x ແລະ y ແມ່ນ ກຳ ນົດດັ່ງຕໍ່ໄປນີ້:
ເລຂາຄະນິດ ໝາຍ ເລກ: ໃນຄະນິດສາດ, ວິຊາ ເລຂາຄະນິດ ແມ່ນຕົວເລກຫຼືສະເລ່ຍ, ເຊິ່ງສະແດງເຖິງທ່າອ່ຽງໃຈກາງຫຼືມູນຄ່າປົກກະຕິຂອງຕົວເລກທີ່ ກຳ ນົດໄວ້ໂດຍການ ນຳ ໃຊ້ຜະລິດຕະພັນຂອງຄຸນຄ່າຂອງພວກເຂົາ. ສະເລ່ຍ geometric ຖືກກໍານົດເປັນ n th root ຜະລິດຕະພັນຂອງຕົວເລກ n, ຕົວຢ່າງ, ສໍາລັບການທີ່ກໍານົດໄວ້ຂອງຕົວເລກ x 1, x 2, ... , x n, ສະເລ່ຍ geometric ແມ່ນກໍານົດເປັນ
Logarithmic ໝາຍ ຄວາມວ່າ: ໃນຄະນິດສາດ, ໂລ ກາສະຕິກໂລກາຕິກ ແມ່ນ ໜ້າ ທີ່ຂອງສອງຕົວເລກທີ່ບໍ່ລົບເຊິ່ງເທົ່າກັບຄວາມແຕກຕ່າງຂອງພວກເຂົາແບ່ງອອກໂດຍ logarithm ຂອງ ຈຳ ນວນຂອງພວກມັນ. ການຄິດໄລ່ນີ້ແມ່ນສາມາດໃຊ້ໄດ້ໃນບັນຫາດ້ານວິສະວະ ກຳ ທີ່ກ່ຽວຂ້ອງກັບຄວາມຮ້ອນແລະການໂອນມວນສານ.
ໜ່ວຍ ງານຕາມເຫດຜົນເລກຄະນິດສາດ: ໃນການຄິດໄລ່ຄອມພິວເຕີ້, ໜ່ວຍ ງານຕາມເຫດຜົນກ່ຽວກັບເລກຄະນິດສາດ (ALU) ແມ່ນວົງຈອນດິຈິຕອນປະສົມປະສານທີ່ເຮັດ ໜ້າ ທີ່ກ່ຽວກັບເລກຄະນິດສາດແລະຂີດຕໍ່ເລກຖານສອງ. ນີ້ແມ່ນກົງກັນຂ້າມກັບຫົວ ໜ່ວຍ ຈຸດທີ່ລອຍຕົວ (FPU), ເຊິ່ງ ດຳ ເນີນງານກ່ຽວກັບຕົວເລກຈຸດລອຍ. ມັນແມ່ນສິ່ງກໍ່ສ້າງພື້ນຖານຂອງວົງຈອນຄອມພິວເຕີ້ຫລາຍປະເພດ, ລວມທັງ ໜ່ວຍ ງານປະມວນຜົນສູນກາງ (CPU) ຂອງຄອມພິວເຕີ້, FPUs, ແລະ ໜ່ວຍ ປະມວນຜົນກາຟິກ (GPUs).
Arithmetic (ເພງ): ເພງ " Arithmetic " ແມ່ນເພງດຽວໂດຍ Brooke Fraser ປ່ອຍອອກມາໃນປີ 2004. ເພງແມ່ນເພງ ທຳ ອິດຂອງ Fraser ໃນງານເປີດຕົວ ສິ່ງທີ່ຄວນເຮັດກັບ Daylight . ຕໍ່ມາບົດເພງດັ່ງກ່າວໄດ້ຖືກລວມເຂົ້າໃນການລວບລວມ ຂໍ້ມູນເພີ່ມເຕີມຂອງ Sony BMG, ເຊິ່ງເປັນຊຸດຂອງເພງຈາກລາຍການ New Zealand Sony BMG.
Arithmetic (ເພງ): ເພງ " Arithmetic " ແມ່ນເພງດຽວໂດຍ Brooke Fraser ປ່ອຍອອກມາໃນປີ 2004. ເພງແມ່ນເພງ ທຳ ອິດຂອງ Fraser ໃນງານເປີດຕົວ ສິ່ງທີ່ຄວນເຮັດກັບ Daylight . ຕໍ່ມາບົດເພງດັ່ງກ່າວໄດ້ຖືກລວມເຂົ້າໃນການລວບລວມ ຂໍ້ມູນເພີ່ມເຕີມຂອງ Sony BMG, ເຊິ່ງເປັນຊຸດຂອງເພງຈາກລາຍການ New Zealand Sony BMG.
ໜ່ວຍ ງານຕາມເຫດຜົນເລກຄະນິດສາດ: ໃນການຄິດໄລ່ຄອມພິວເຕີ້, ໜ່ວຍ ງານຕາມເຫດຜົນກ່ຽວກັບເລກຄະນິດສາດ (ALU) ແມ່ນວົງຈອນດິຈິຕອນປະສົມປະສານທີ່ເຮັດ ໜ້າ ທີ່ກ່ຽວກັບເລກຄະນິດສາດແລະຂີດຕໍ່ເລກຖານສອງ. ນີ້ແມ່ນກົງກັນຂ້າມກັບຫົວ ໜ່ວຍ ຈຸດທີ່ລອຍຕົວ (FPU), ເຊິ່ງ ດຳ ເນີນງານກ່ຽວກັບຕົວເລກຈຸດລອຍ. ມັນແມ່ນສິ່ງກໍ່ສ້າງພື້ນຖານຂອງວົງຈອນຄອມພິວເຕີ້ຫລາຍປະເພດ, ລວມທັງ ໜ່ວຍ ງານປະມວນຜົນສູນກາງ (CPU) ຂອງຄອມພິວເຕີ້, FPUs, ແລະ ໜ່ວຍ ປະມວນຜົນກາຟິກ (GPUs).
ເລຂາຄະນິດກ່ຽວກັບເລກຄະນິດສາດ: ໃນຄະນິດສາດ, ເລຂາຄະນິດສາດ ແມ່ນປະມານການ ນຳ ໃຊ້ເຕັກນິກຈາກເລຂາຄະນິດຄະນິດສາດເຖິງບັນຫາໃນທິດສະດີເລກ. ເລຂາຄະນິດກ່ຽວກັບເລກຄະນິດສາດແມ່ນເປັນຈຸດສູນກາງປະມານເລຂາຄະນິດ Diophantine, ການສຶກສາຈຸດທີ່ສົມເຫດສົມຜົນຂອງແນວພັນພຶດຊະຄະນິດ.
ທິດສະດີ Arakelov: ໃນຄະນິດສາດ, ທິດສະດີ Arakelov ແມ່ນວິທີການທາງເລຂາຄະນິດ Diophantine, ຊື່ວ່າ Suren Arakelov. ມັນຖືກນໍາໃຊ້ເພື່ອສຶກສາສົມຜົນ Diophantine ໃນຂະຫນາດທີ່ສູງກວ່າ.
ລະຫັດເລກຄະນິດສາດ: ການຂຽນລະຫັດ Arithmetic ( AC ) ແມ່ນຮູບແບບຂອງການເຂົ້າລະຫັດແບບ entropy ທີ່ໃຊ້ໃນການບີບອັດຂໍ້ມູນທີ່ບໍ່ມີການສູນເສຍ. ໂດຍປົກກະຕິ, ສາຍອັກຂະລະຂອງຕົວລະຄອນເຊັ່ນ: ຄຳ ວ່າ "ສະບາຍດີຢູ່ທີ່ນັ້ນ" ແມ່ນຕົວແທນໂດຍໃຊ້ ຈຳ ນວນບິດຕໍ່ຕົວອັກສອນ, ຄືກັບລະຫັດ ASCII. ເມື່ອສາຍສະຕິງຖືກປ່ຽນເປັນລະບົບພາສາເລກຄະນິດສາດ, ຕົວອັກສອນທີ່ໃຊ້ເລື້ອຍໆຈະຖືກເກັບໄວ້ດ້ວຍບິດ ໜ້ອຍ ແລະຕົວອັກສອນທີ່ບໍ່ຄ່ອຍຈະເກີດຂື້ນຈະຖືກເກັບຮັກສາໄວ້ດ້ວຍກະຕ່າເພີ່ມເຕີມ, ສົ່ງຜົນໃຫ້ມີ ຈຳ ນວນນ້ອຍທີ່ໃຊ້ໃນ ຈຳ ນວນທັງ ໝົດ. ການເຂົ້າລະຫັດເລກຄະນິດສາດແຕກຕ່າງຈາກຮູບແບບອື່ນໆຂອງລະຫັດເຂົ້າລະຫັດເຊັ່ນ Huffman coding ໃນນັ້ນແທນທີ່ຈະແຍກການປ້ອນຂໍ້ມູນເຂົ້າໃນສັນຍາລັກຂອງອົງປະກອບແລະປ່ຽນແທນແຕ່ລະລະຫັດ, ການເຂົ້າລະຫັດເລກຄະນິດສາດເຂົ້າລະຫັດຂໍ້ຄວາມທັງ ໝົດ ເປັນຕົວເລກດຽວ, ສ່ວນອັດຕາສ່ວນທີ່ຖືກຕ້ອງໂດຍກົງ q , ບ່ອນທີ່ 0.0 ≤ q <1.0 . ມັນສະແດງຂໍ້ມູນໃນປະຈຸບັນເປັນຊ່ວງ, ກຳ ນົດໂດຍສອງຕົວເລກ. ຄອບຄົວຂອງລະຫັດປ້ອນຂໍ້ມູນ entropy ທີ່ຜ່ານມາເອີ້ນວ່າລະບົບ ຈຳ ນວນບໍ່ເທົ່າກັນຊ່ວຍໃຫ້ມີການຈັດຕັ້ງປະຕິບັດໄດ້ໄວຂຶ້ນຍ້ອນການປະຕິບັດໂດຍກົງໃສ່ຕົວເລກ ທຳ ມະຊາດດຽວທີ່ເປັນຕົວແທນຂອງຂໍ້ມູນໃນປະຈຸບັນ
ເລກຄະນິດສາດແລະເລຂາຄະນິດ Frobenius: ໃນຄະນິດສາດ, ການ endomorphism Frobenius ຖືກກໍານົດໄວ້ໃນ R ວົງ commutative ທີ່ມີ p ລັກສະນະ, ບ່ອນທີ່ p ເປັນຈໍານວນເສພາ. ຄື, ການφການສ້າງແຜນທີ່ທີ່ໃຊ້ເວລາ r ໃນ R ເພື່ອ r p ເປັນ endomorphism ວົງການ R.
ພະຍາດ endomorphism Frobenius: ໃນພຶດຊະຄະນິດຄະນິດສາດແລະທິດສະດີພາກສະ ໜາມ, Frobenius endomorphism ແມ່ນ endomorphism ພິເສດຂອງວົງແຫວນ commutative ທີ່ມີ p ລັກສະນະຕົ້ນ, ເປັນຫ້ອງຮຽນທີ່ ສຳ ຄັນເຊິ່ງລວມມີບັນດາຂົງເຂດທີ່ ຈຳ ກັດ. endomorphism ມີແຜນທີ່ທຸກໆອົງປະກອບໃຫ້ກັບພະລັງງານ p -th ຂອງມັນ. ໃນສະພາບການທີ່ແນ່ນອນມັນແມ່ນເລື່ອງອັດຕະໂນມັດ, ແຕ່ນີ້ບໍ່ແມ່ນຄວາມຈິງໂດຍທົ່ວໄປ.
ກຸ່ມ Arithmetic Fuchsian: ກຸ່ມ Arithmetic Fuchsian ແມ່ນຊັ້ນຮຽນພິເສດຂອງກຸ່ມ Fuchsian ທີ່ສ້າງໂດຍໃຊ້ ຄຳ ສັ່ງໃນ alaterbras quaternion. ພວກເຂົາແມ່ນຕົວຢ່າງໂດຍສະເພາະຂອງກຸ່ມເລກຄະນິດສາດ. ຕົວຢ່າງຕົ້ນແບບຂອງກຸ່ມ Fuchsian ກ່ຽວກັບເລກຄະນິດສາດແມ່ນກຸ່ມແບບໂມດູນ . ພວກເຂົາ, ແລະພື້ນຜິວ hyperbolic ທີ່ກ່ຽວຂ້ອງກັບການປະຕິບັດງານຂອງພວກເຂົາໃນຍົນ hyperbolic ມັກຈະສະແດງພຶດຕິ ກຳ ທີ່ເປັນປົກກະຕິໂດຍສະເພາະໃນກຸ່ມ Fuchsian ແລະ ໜ້າ hyperbolic.
ເລຂາຄະນິດກ່ຽວກັບເລກຄະນິດສາດ: ໃນຄະນິດສາດ, ເລຂາຄະນິດສາດ ແມ່ນປະມານການ ນຳ ໃຊ້ເຕັກນິກຈາກເລຂາຄະນິດຄະນິດສາດເຖິງບັນຫາໃນທິດສະດີເລກ. ເລຂາຄະນິດກ່ຽວກັບເລກຄະນິດສາດແມ່ນເປັນຈຸດສູນກາງປະມານເລຂາຄະນິດ Diophantine, ການສຶກສາຈຸດທີ່ສົມເຫດສົມຜົນຂອງແນວພັນພຶດຊະຄະນິດ.
ເລກຄະນິດສາດ IF: ຄຳ ຖະແຫຼງ ກ່ຽວກັບເລກຄະນິດສາດ IF ແມ່ນ ຄຳ ຖະແຫຼງເງື່ອນໄຂກ່ຽວກັບເລກຄະນິດສາດ, ເຊິ່ງເຫັນໄດ້ໃນການປ່ອຍ Fortran ຄັ້ງ ທຳ ອິດໃນປີ 1957, ແລະພົບໃນທຸກລຸ້ນຕໍ່ມາ, ແລະບາງພາສາການຂຽນໂປຼແກຼມອື່ນໆ, ເຊັ່ນ FOCAL. ບໍ່ຄືກັບ ຄຳ ເວົ້າ IF ຢ່າງມີເຫດຜົນທີ່ເຫັນໃນພາສາອື່ນໆ, ຄຳ ຖະແຫຼງທີ່ Fortran ກຳ ນົດສາມສາຂາທີ່ແຕກຕ່າງກັນຂື້ນຢູ່ກັບວ່າຜົນຂອງການສະແດງອອກແມ່ນລົບ, ສູນ, ຫລືບວກ, ໃນ ຄຳ ສັ່ງທີ່ກ່າວໄວ້, ຂຽນເປັນ:
ຕຶກອາຄານ hyperbolic 3-manifold: ໃນຄະນິດສາດ, ມີຄວາມຊັດເຈນກວ່າໃນທິດສະດີກຸ່ມແລະເລຂາຄະນິດ hyperbolic, ກຸ່ມ Arithmetic Kleinian ແມ່ນຊັ້ນຮຽນພິເສດຂອງກຸ່ມ Kleinian ທີ່ສ້າງໂດຍໃຊ້ ຄຳ ສັ່ງໃນ alaterbras quaternion. ພວກເຂົາແມ່ນຕົວຢ່າງໂດຍສະເພາະຂອງກຸ່ມເລກຄະນິດສາດ. ຕົວຊີ້ວັດ hyperbolic ສາມແບບ ເປັນຕົວເລກຂອງ ຈຳ ນວນອະວະກາດ hyperbolic ໂດຍກຸ່ມ Kleinian ເລກຄະນິດສາດ. manifold ເຫຼົ່ານີ້ປະກອບມີຕົວຢ່າງທີ່ສວຍງາມໂດຍສະເພາະບາງຢ່າງ.
ໜ່ວຍ ງານຕາມເຫດຜົນເລກຄະນິດສາດ: ໃນການຄິດໄລ່ຄອມພິວເຕີ້, ໜ່ວຍ ງານຕາມເຫດຜົນກ່ຽວກັບເລກຄະນິດສາດ (ALU) ແມ່ນວົງຈອນດິຈິຕອນປະສົມປະສານທີ່ເຮັດ ໜ້າ ທີ່ກ່ຽວກັບເລກຄະນິດສາດແລະຂີດຕໍ່ເລກຖານສອງ. ນີ້ແມ່ນກົງກັນຂ້າມກັບຫົວ ໜ່ວຍ ຈຸດທີ່ລອຍຕົວ (FPU), ເຊິ່ງ ດຳ ເນີນງານກ່ຽວກັບຕົວເລກຈຸດລອຍ. ມັນແມ່ນສິ່ງກໍ່ສ້າງພື້ນຖານຂອງວົງຈອນຄອມພິວເຕີ້ຫລາຍປະເພດ, ລວມທັງ ໜ່ວຍ ງານປະມວນຜົນສູນກາງ (CPU) ຂອງຄອມພິວເຕີ້, FPUs, ແລະ ໜ່ວຍ ປະມວນຜົນກາຟິກ (GPUs).
ເລກຄະນິດສາດ: ໃນຄະນິດສາດແລະສະຖິຕິ, ຄວາມ ໝາຍ ເລກຄະນິດສາດ , ຫຼືພຽງແຕ່ຄ່າສະເລ່ຍຫຼື ສະເລ່ຍ , ແມ່ນການລວມຕົວເລກຂອງຕົວເລກທີ່ແບ່ງຕາມການນັບຂອງຕົວເລກໃນການເກັບ. ການລວບລວມມັກຈະເປັນຊຸດຂອງຜົນຂອງການທົດລອງຫຼືການສຶກສາການສັງເກດການ, ຫຼືມັກຈະເປັນຊຸດຂອງຜົນໄດ້ຮັບຈາກການ ສຳ ຫຼວດ. ຄຳ ວ່າ "ຄວາມ ໝາຍ ເລກຄະນິດສາດ" ແມ່ນມັກໃນບາງສະພາບການໃນຄະນິດສາດແລະສະຖິຕິ, ເພາະວ່າມັນຊ່ວຍແຍກແຍະມັນຈາກວິທີອື່ນ, ເຊັ່ນ: ຄວາມ ໝາຍ ຂອງເລຂາຄະນິດແລະຄວາມ ໝາຍ ທີ່ມີຄວາມ ໝາຍ.
ຄວາມບໍ່ສະເຫມີພາບຂອງເລກຄະນິດສາດແລະເລຂາຄະນິດ: ໃນທາງຄະນິດສາດ, ຄວາມບໍ່ສະ ເໝີ ພາບຂອງວິທີເລກຄະນິດສາດແລະເລຂາຄະນິດ , ຫຼືເວົ້າສັ້ນໆກວ່າ ຄວາມບໍ່ສະ ເໝີ ພາບ AM – GM , ລະບຸວ່າຕົວເລກເລກຄະນິດສາດຂອງບັນຊີຂອງຕົວເລກຕົວຈິງທີ່ບໍ່ລົບແມ່ນສູງກວ່າຫຼືເທົ່າກັບຄ່າເລຂາຄະນິດເລຂາຄະນິດດຽວກັນ; ແລະໃນຕໍ່ ໜ້າ, ທັງສອງວິທີແມ່ນເທົ່າທຽມກັນຖ້າວ່າແລະທຸກໆຕົວເລກໃນບັນຊີແມ່ນເທົ່າກັນ.
ຄວາມຄືບ ໜ້າ ເລກຄະນິດສາດ: ຄວາມຄືບ ໜ້າ ກ່ຽວກັບເລກຄະນິດສາດ (AP) ຫຼື ລຳ ດັບເລກຄະນິດສາດ ແມ່ນ ລຳ ດັບຂອງຕົວເລກດັ່ງກ່າວວ່າຄວາມແຕກຕ່າງລະຫວ່າງ ຄຳ ຕໍ່ເນື່ອງແມ່ນຄົງທີ່. ຍົກຕົວຢ່າງ, ລຳ ດັບ 5, 7, 9, 11, 13, 15,. .. ແມ່ນຄວາມຄືບ ໜ້າ ເລກຄະນິດສາດທີ່ມີຄວາມແຕກຕ່າງທົ່ວໄປຂອງ 2.
ທິດສະດີ Arakelov: ໃນຄະນິດສາດ, ທິດສະດີ Arakelov ແມ່ນວິທີການທາງເລຂາຄະນິດ Diophantine, ຊື່ວ່າ Suren Arakelov. ມັນຖືກນໍາໃຊ້ເພື່ອສຶກສາສົມຜົນ Diophantine ໃນຂະຫນາດທີ່ສູງກວ່າ.
ທິດສະດີ Arakelov: ໃນຄະນິດສາດ, ທິດສະດີ Arakelov ແມ່ນວິທີການທາງເລຂາຄະນິດ Diophantine, ຊື່ວ່າ Suren Arakelov. ມັນຖືກນໍາໃຊ້ເພື່ອສຶກສາສົມຜົນ Diophantine ໃນຂະຫນາດທີ່ສູງກວ່າ.
ຄວາມຄືບ ໜ້າ ເລກຄະນິດສາດ: ຄວາມຄືບ ໜ້າ ກ່ຽວກັບເລກຄະນິດສາດ (AP) ຫຼື ລຳ ດັບເລກຄະນິດສາດ ແມ່ນ ລຳ ດັບຂອງຕົວເລກດັ່ງກ່າວວ່າຄວາມແຕກຕ່າງລະຫວ່າງ ຄຳ ຕໍ່ເນື່ອງແມ່ນຄົງທີ່. ຍົກຕົວຢ່າງ, ລຳ ດັບ 5, 7, 9, 11, 13, 15,. .. ແມ່ນຄວາມຄືບ ໜ້າ ເລກຄະນິດສາດທີ່ມີຄວາມແຕກຕ່າງທົ່ວໄປຂອງ 2.
ດ້ານເລກຄະນິດສາດ: ໃນຄະນິດສາດ, ພື້ນຜິວເລກຄະນິດສາດ ເໜືອ ໂດເມນ Dedekind R ທີ່ມີສ່ວນປະກອບ ແມ່ນວັດຖຸເລຂາຄະນິດທີ່ມີມິຕິ ທຳ ມະດາ ໜຶ່ງ ໜ່ວຍ, ແລະອີກ ໜຶ່ງ ມິຕິອື່ນທີ່ສະ ໜອງ ໂດຍນິຍາມຂອງນາຍົກລັດຖະມົນຕີ. ໃນເວລາທີ່ R ແມ່ນແຫວນຂອງເລກເຕັມ Z , ຄວາມຕັ້ງໃຈນີ້ຂື້ນກັບລະດັບທີ່ດີທີ່ສຸດ ສຳ ລັບລະດັບສະເພາະ ( Z ) ທີ່ຖືກເຫັນວ່າປຽບທຽບກັບເສັ້ນ. ພື້ນຜິວເລກຄະນິດສາດເກີດຂື້ນຕາມ ທຳ ມະຊາດໃນເລຂາຄະນິດ diophantine, ເມື່ອເສັ້ນໂຄ້ງ algebraic ຖືກ ກຳ ນົດໃນ K ແມ່ນຄິດວ່າມີການຫຼຸດລົງໃນພື້ນທີ່ R / P , ບ່ອນທີ່ P ແມ່ນສິ່ງທີ່ດີທີ່ສຸດຂອງ R , ສຳ ລັບເກືອບທັງ ໝົດ P ; ແລະມີປະໂຫຍດໃນການ ກຳ ນົດສິ່ງທີ່ຄວນຈະເກີດຂື້ນກ່ຽວກັບຂະບວນການຫຼຸດລົງເປັນ R / P ເມື່ອວິທີການທີ່ໂງ່ທີ່ສຸດເຮັດໃຫ້ບໍ່ມີຄວາມ ໝາຍ.
ການຊື້ຂາຍແບບມີລິຂະສິດ: ການຊື້ຂາຍແບບ Algorithmic ແມ່ນວິທີການ ດຳ ເນີນການ ຄຳ ສັ່ງໂດຍ ນຳ ໃຊ້ ຄຳ ແນະ ນຳ ກ່ຽວກັບການຊື້ຂາຍທີ່ມີໂປແກຼມລ່ວງ ໜ້າ ໂດຍອັດຕະໂນມັດກວມເອົາຕົວແປຕ່າງໆເຊັ່ນ: ເວລາ, ລາຄາແລະປະລິມານ. ການຊື້ຂາຍແບບນີ້ພະຍາຍາມເລັ່ງຄວາມໄວແລະຊັບພະຍາກອນຄອມພິວເຕີ້ທີ່ກ່ຽວຂ້ອງກັບພໍ່ຄ້າມະນຸດ. ໃນສະຕະວັດທີຊາວ, ການຊື້ຂາຍແບບມີ ກຳ ໄລໄດ້ຮັບຜົນກະທົບຈາກທັງພໍ່ຄ້າຂາຍຍ່ອຍແລະສະຖາບັນ. ມັນໄດ້ຖືກນໍາໃຊ້ຢ່າງກວ້າງຂວາງໂດຍທະນາຄານການລົງທືນ, ກອງທຶນບໍານານ, ກອງທຶນເຊິ່ງກັນແລະກັນແລະກອງທຶນ hedge ເຊິ່ງອາດຈະຕ້ອງການເຜີຍແຜ່ການປະຕິບັດຄໍາສັ່ງທີ່ໃຫຍ່ກວ່າຫຼືປະຕິບັດການຄ້າທີ່ໄວເກີນໄປເພື່ອໃຫ້ພໍ່ຄ້າມະນຸດມີປະຕິກິລິຍາ. ການສຶກສາໃນປີ 2019 ໄດ້ສະແດງໃຫ້ເຫັນວ່າປະມານ 92% ຂອງການຊື້ຂາຍໃນຕະຫຼາດ Forex ແມ່ນປະຕິບັດໂດຍລະບົບການຊື້ຂາຍຫຼາຍກວ່າມະນຸດ.
ເລຂາຄະນິດກ່ຽວກັບເລກຄະນິດສາດ: ໃນຄະນິດສາດ, ເລຂາຄະນິດສາດ ແມ່ນປະມານການ ນຳ ໃຊ້ເຕັກນິກຈາກເລຂາຄະນິດຄະນິດສາດເຖິງບັນຫາໃນທິດສະດີເລກ. ເລຂາຄະນິດກ່ຽວກັບເລກຄະນິດສາດແມ່ນເປັນຈຸດສູນກາງປະມານເລຂາຄະນິດ Diophantine, ການສຶກສາຈຸດທີ່ສົມເຫດສົມຜົນຂອງແນວພັນພຶດຊະຄະນິດ.
ໜ່ວຍ ງານຕາມເຫດຜົນເລກຄະນິດສາດ: ໃນການຄິດໄລ່ຄອມພິວເຕີ້, ໜ່ວຍ ງານຕາມເຫດຜົນກ່ຽວກັບເລກຄະນິດສາດ (ALU) ແມ່ນວົງຈອນດິຈິຕອນປະສົມປະສານທີ່ເຮັດ ໜ້າ ທີ່ກ່ຽວກັບເລກຄະນິດສາດແລະຂີດຕໍ່ເລກຖານສອງ. ນີ້ແມ່ນກົງກັນຂ້າມກັບຫົວ ໜ່ວຍ ຈຸດທີ່ລອຍຕົວ (FPU), ເຊິ່ງ ດຳ ເນີນງານກ່ຽວກັບຕົວເລກຈຸດລອຍ. ມັນແມ່ນສິ່ງກໍ່ສ້າງພື້ນຖານຂອງວົງຈອນຄອມພິວເຕີ້ຫລາຍປະເພດ, ລວມທັງ ໜ່ວຍ ງານປະມວນຜົນສູນກາງ (CPU) ຂອງຄອມພິວເຕີ້, FPUs, ແລະ ໜ່ວຍ ປະມວນຜົນກາຟິກ (GPUs).
ເລກຄະນິດສາດແລະເລຂາຄະນິດ Frobenius: ໃນຄະນິດສາດ, ການ endomorphism Frobenius ຖືກກໍານົດໄວ້ໃນ R ວົງ commutative ທີ່ມີ p ລັກສະນະ, ບ່ອນທີ່ p ເປັນຈໍານວນເສພາ. ຄື, ການφການສ້າງແຜນທີ່ທີ່ໃຊ້ເວລາ r ໃນ R ເພື່ອ r p ເປັນ endomorphism ວົງການ R.
ເລກຄະນິດສາດແລະເລຂາຄະນິດ Frobenius: ໃນຄະນິດສາດ, ການ endomorphism Frobenius ຖືກກໍານົດໄວ້ໃນ R ວົງ commutative ທີ່ມີ p ລັກສະນະ, ບ່ອນທີ່ p ເປັນຈໍານວນເສພາ. ຄື, ການφການສ້າງແຜນທີ່ທີ່ໃຊ້ເວລາ r ໃນ R ເພື່ອ r p ເປັນ endomorphism ວົງການ R.
ຖາປັດຕະຍະ ກຳ ນົດການສອນ: ໃນວິທະຍາສາດຄອມພິວເຕີ, ສະຖາປັດຕະຍະ ກຳ ກຳ ນົດການສິດສອນ ( ISA ) ແມ່ນຮູບແບບທີ່ບໍ່ມີຕົວຕົນຂອງຄອມພິວເຕີ. ມັນກໍ່ຖືກເອີ້ນວ່າ ສະຖາປັດຕະຍະ ກຳ ຫລື ສະຖາປັດຕະຍະ ກຳ ຄອມພິວເຕີ . ການປະຕິບັດຕົວຈິງຂອງ ISA ເຊັ່ນ ໜ່ວຍ ງານປະມວນຜົນສູນກາງ (CPU) ຖືກເອີ້ນວ່າການ ຈັດຕັ້ງປະຕິບັດ .
ໜ່ວຍ ງານຕາມເຫດຜົນເລກຄະນິດສາດ: ໃນການຄິດໄລ່ຄອມພິວເຕີ້, ໜ່ວຍ ງານຕາມເຫດຜົນກ່ຽວກັບເລກຄະນິດສາດ (ALU) ແມ່ນວົງຈອນດິຈິຕອນປະສົມປະສານທີ່ເຮັດ ໜ້າ ທີ່ກ່ຽວກັບເລກຄະນິດສາດແລະຂີດຕໍ່ເລກຖານສອງ. ນີ້ແມ່ນກົງກັນຂ້າມກັບຫົວ ໜ່ວຍ ຈຸດທີ່ລອຍຕົວ (FPU), ເຊິ່ງ ດຳ ເນີນງານກ່ຽວກັບຕົວເລກຈຸດລອຍ. ມັນແມ່ນສິ່ງກໍ່ສ້າງພື້ນຖານຂອງວົງຈອນຄອມພິວເຕີ້ຫລາຍປະເພດ, ລວມທັງ ໜ່ວຍ ງານປະມວນຜົນສູນກາງ (CPU) ຂອງຄອມພິວເຕີ້, FPUs, ແລະ ໜ່ວຍ ປະມວນຜົນກາຟິກ (GPUs).
ໜ່ວຍ ງານຕາມເຫດຜົນເລກຄະນິດສາດ: ໃນການຄິດໄລ່ຄອມພິວເຕີ້, ໜ່ວຍ ງານຕາມເຫດຜົນກ່ຽວກັບເລກຄະນິດສາດ (ALU) ແມ່ນວົງຈອນດິຈິຕອນປະສົມປະສານທີ່ເຮັດ ໜ້າ ທີ່ກ່ຽວກັບເລກຄະນິດສາດແລະຂີດຕໍ່ເລກຖານສອງ. ນີ້ແມ່ນກົງກັນຂ້າມກັບຫົວ ໜ່ວຍ ຈຸດທີ່ລອຍຕົວ (FPU), ເຊິ່ງ ດຳ ເນີນງານກ່ຽວກັບຕົວເລກຈຸດລອຍ. ມັນແມ່ນສິ່ງກໍ່ສ້າງພື້ນຖານຂອງວົງຈອນຄອມພິວເຕີ້ຫລາຍປະເພດ, ລວມທັງ ໜ່ວຍ ງານປະມວນຜົນສູນກາງ (CPU) ຂອງຄອມພິວເຕີ້, FPUs, ແລະ ໜ່ວຍ ປະມວນຜົນກາຟິກ (GPUs).
ໜ່ວຍ ງານຕາມເຫດຜົນເລກຄະນິດສາດ: ໃນການຄິດໄລ່ຄອມພິວເຕີ້, ໜ່ວຍ ງານຕາມເຫດຜົນກ່ຽວກັບເລກຄະນິດສາດ (ALU) ແມ່ນວົງຈອນດິຈິຕອນປະສົມປະສານທີ່ເຮັດ ໜ້າ ທີ່ກ່ຽວກັບເລກຄະນິດສາດແລະຂີດຕໍ່ເລກຖານສອງ. ນີ້ແມ່ນກົງກັນຂ້າມກັບຫົວ ໜ່ວຍ ຈຸດທີ່ລອຍຕົວ (FPU), ເຊິ່ງ ດຳ ເນີນງານກ່ຽວກັບຕົວເລກຈຸດລອຍ. ມັນແມ່ນສິ່ງກໍ່ສ້າງພື້ນຖານຂອງວົງຈອນຄອມພິວເຕີ້ຫລາຍປະເພດ, ລວມທັງ ໜ່ວຍ ງານປະມວນຜົນສູນກາງ (CPU) ຂອງຄອມພິວເຕີ້, FPUs, ແລະ ໜ່ວຍ ປະມວນຜົນກາຟິກ (GPUs).
ສະເລ່ຍ: ໃນພາສາທີ່ໃຊ້ເວົ້າລວມ, ສະເລ່ຍ ແມ່ນຕົວເລກດຽວທີ່ຖືກປະຕິບັດເປັນຕົວແທນຂອງບັນຊີລາຍຊື່ທີ່ບໍ່ແມ່ນຫວ່າງ. ແນວຄິດທີ່ແຕກຕ່າງກັນຂອງຄ່າສະເລ່ຍແມ່ນໃຊ້ໃນສະພາບການທີ່ແຕກຕ່າງກັນ. ສ່ວນຫຼາຍ "ສະເລ່ຍ" ໝາຍ ເຖິງຕົວເລກເລກຄະນິດສາດ, ຜົນລວມຂອງຕົວເລກທີ່ແບ່ງອອກໂດຍ ຈຳ ນວນຕົວເລກທີ່ໄດ້ຖືກສະເລ່ຍແລ້ວ. ໃນສະຖິຕິ, ສະເລ່ຍ, ປານກາງ, ແລະຮູບແບບແມ່ນເປັນທີ່ຮູ້ກັນວ່າເປັນມາດຕະການຂອງແນວໂນ້ມສູນກາງ, ແລະໃນການ ນຳ ໃຊ້ແບບລ້າໆ, ສິ່ງເຫຼົ່ານີ້ອາດຈະເອີ້ນວ່າ ມູນຄ່າສະເລ່ຍ .
ທະນາຍຄວາມກ່ຽວກັບເລກຄະນິດສາດ: ໃນຄະນິດສາດການພັກຜ່ອນ, ໃບ ບິນທະນາຍຄວາມກ່ຽວກັບເລກຄະນິດສາດ ໃຫ້ວິທີການເລຂາຄະນິດເພື່ອ ກຳ ນົດຕົວເລກທະວີຄູນທີ່ມີຕົວເລກແລະຕົວເລກທີ່ ທຳ ມະດາທີ່ສຸດທີ່ສຸດຂອງສອງຕົວເລກ ທຳ ມະຊາດໂດຍການ ນຳ ໃຊ້ການສະທ້ອນພາຍໃນຮູບສີ່ຫລ່ຽມເຊິ່ງສອງຂ້າງແມ່ນຕົວເລກສອງຕົວເລກ. ນີ້ແມ່ນຕົວຢ່າງທີ່ງ່າຍຂອງການວິເຄາະເສັ້ນທາງຂອງບັນດານັກບິນທະນາຄານແບບເຄື່ອນໄຫວ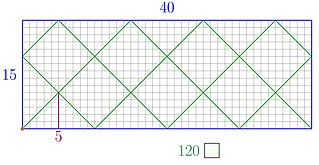
ຄວາມສັບສົນຂອງວົງຈອນເລກຄະນິດສາດ: ໃນທິດສະດີຄວາມສັບສົນດ້ານຄອມພິວເຕີ້, ວົງຈອນເລກຄະນິດສາດ ແມ່ນຮູບແບບມາດຕະຖານ ສຳ ລັບຄອມພິວເຕີ້ຄອມພີວເຕີ້. ຢ່າງເປັນທາງການ, ວົງຈອນເລກຄະນິດສາດໃຊ້ເວລາເປັນວັດສະດຸປ້ອນທັງຕົວແປຫລືຕົວເລກແລະຖືກອະນຸຍາດໃຫ້ເພີ່ມຫລືຄູນສອງ ສຳ ນວນທີ່ມັນໄດ້ ຄຳ ນວນມາແລ້ວ. ວົງຈອນເລກຄະນິດສາດໃຫ້ເປັນວິທີທາງການທີ່ຈະເຂົ້າໃຈຄວາມສັບສົນຂອງຄອມພິວເຕີ້ຄອມພີວເຕີ້. ປະເພດ ຄຳ ຖາມພື້ນຖານໃນການຄົ້ນຄ້ວາເສັ້ນນີ້ແມ່ນ "ວິທີໃດທີ່ມີປະສິດຕິພາບສູງສຸດໃນການ ຄຳ ນວນ polynomial ທີ່ໃຫ້ ? "
ຄວາມສັບສົນຂອງວົງຈອນເລກຄະນິດສາດ: ໃນທິດສະດີຄວາມສັບສົນດ້ານຄອມພິວເຕີ້, ວົງຈອນເລກຄະນິດສາດ ແມ່ນຮູບແບບມາດຕະຖານ ສຳ ລັບຄອມພິວເຕີ້ຄອມພີວເຕີ້. ຢ່າງເປັນທາງການ, ວົງຈອນເລກຄະນິດສາດໃຊ້ເວລາເປັນວັດສະດຸປ້ອນທັງຕົວແປຫລືຕົວເລກແລະຖືກອະນຸຍາດໃຫ້ເພີ່ມຫລືຄູນສອງ ສຳ ນວນທີ່ມັນໄດ້ ຄຳ ນວນມາແລ້ວ. ວົງຈອນເລກຄະນິດສາດໃຫ້ເປັນວິທີທາງການທີ່ຈະເຂົ້າໃຈຄວາມສັບສົນຂອງຄອມພິວເຕີ້ຄອມພີວເຕີ້. ປະເພດ ຄຳ ຖາມພື້ນຖານໃນການຄົ້ນຄ້ວາເສັ້ນນີ້ແມ່ນ "ວິທີໃດທີ່ມີປະສິດຕິພາບສູງສຸດໃນການ ຄຳ ນວນ polynomial ທີ່ໃຫ້ ? "
ຄວາມສັບສົນຂອງວົງຈອນເລກຄະນິດສາດ: ໃນທິດສະດີຄວາມສັບສົນດ້ານຄອມພິວເຕີ້, ວົງຈອນເລກຄະນິດສາດ ແມ່ນຮູບແບບມາດຕະຖານ ສຳ ລັບຄອມພິວເຕີ້ຄອມພີວເຕີ້. ຢ່າງເປັນທາງການ, ວົງຈອນເລກຄະນິດສາດໃຊ້ເວລາເປັນວັດສະດຸປ້ອນທັງຕົວແປຫລືຕົວເລກແລະຖືກອະນຸຍາດໃຫ້ເພີ່ມຫລືຄູນສອງ ສຳ ນວນທີ່ມັນໄດ້ ຄຳ ນວນມາແລ້ວ. ວົງຈອນເລກຄະນິດສາດໃຫ້ເປັນວິທີທາງການທີ່ຈະເຂົ້າໃຈຄວາມສັບສົນຂອງຄອມພິວເຕີ້ຄອມພີວເຕີ້. ປະເພດ ຄຳ ຖາມພື້ນຖານໃນການຄົ້ນຄ້ວາເສັ້ນນີ້ແມ່ນ "ວິທີໃດທີ່ມີປະສິດຕິພາບສູງສຸດໃນການ ຄຳ ນວນ polynomial ທີ່ໃຫ້ ? "
ຄວາມສັບສົນຂອງວົງຈອນເລກຄະນິດສາດ: ໃນທິດສະດີຄວາມສັບສົນດ້ານຄອມພິວເຕີ້, ວົງຈອນເລກຄະນິດສາດ ແມ່ນຮູບແບບມາດຕະຖານ ສຳ ລັບຄອມພິວເຕີ້ຄອມພີວເຕີ້. ຢ່າງເປັນທາງການ, ວົງຈອນເລກຄະນິດສາດໃຊ້ເວລາເປັນວັດສະດຸປ້ອນທັງຕົວແປຫລືຕົວເລກແລະຖືກອະນຸຍາດໃຫ້ເພີ່ມຫລືຄູນສອງ ສຳ ນວນທີ່ມັນໄດ້ ຄຳ ນວນມາແລ້ວ. ວົງຈອນເລກຄະນິດສາດໃຫ້ເປັນວິທີທາງການທີ່ຈະເຂົ້າໃຈຄວາມສັບສົນຂອງຄອມພິວເຕີ້ຄອມພີວເຕີ້. ປະເພດ ຄຳ ຖາມພື້ນຖານໃນການຄົ້ນຄ້ວາເສັ້ນນີ້ແມ່ນ "ວິທີໃດທີ່ມີປະສິດຕິພາບສູງສຸດໃນການ ຄຳ ນວນ polynomial ທີ່ໃຫ້ ? "
ລະຫັດເລກຄະນິດສາດ: ການຂຽນລະຫັດ Arithmetic ( AC ) ແມ່ນຮູບແບບຂອງການເຂົ້າລະຫັດແບບ entropy ທີ່ໃຊ້ໃນການບີບອັດຂໍ້ມູນທີ່ບໍ່ມີການສູນເສຍ. ໂດຍປົກກະຕິ, ສາຍອັກຂະລະຂອງຕົວລະຄອນເຊັ່ນ: ຄຳ ວ່າ "ສະບາຍດີຢູ່ທີ່ນັ້ນ" ແມ່ນຕົວແທນໂດຍໃຊ້ ຈຳ ນວນບິດຕໍ່ຕົວອັກສອນ, ຄືກັບລະຫັດ ASCII. ເມື່ອສາຍສະຕິງຖືກປ່ຽນເປັນລະບົບພາສາເລກຄະນິດສາດ, ຕົວອັກສອນທີ່ໃຊ້ເລື້ອຍໆຈະຖືກເກັບໄວ້ດ້ວຍບິດ ໜ້ອຍ ແລະຕົວອັກສອນທີ່ບໍ່ຄ່ອຍຈະເກີດຂື້ນຈະຖືກເກັບຮັກສາໄວ້ດ້ວຍກະຕ່າເພີ່ມເຕີມ, ສົ່ງຜົນໃຫ້ມີ ຈຳ ນວນນ້ອຍທີ່ໃຊ້ໃນ ຈຳ ນວນທັງ ໝົດ. ການເຂົ້າລະຫັດເລກຄະນິດສາດແຕກຕ່າງຈາກຮູບແບບອື່ນໆຂອງລະຫັດເຂົ້າລະຫັດເຊັ່ນ Huffman coding ໃນນັ້ນແທນທີ່ຈະແຍກການປ້ອນຂໍ້ມູນເຂົ້າໃນສັນຍາລັກຂອງອົງປະກອບແລະປ່ຽນແທນແຕ່ລະລະຫັດ, ການເຂົ້າລະຫັດເລກຄະນິດສາດເຂົ້າລະຫັດຂໍ້ຄວາມທັງ ໝົດ ເປັນຕົວເລກດຽວ, ສ່ວນອັດຕາສ່ວນທີ່ຖືກຕ້ອງໂດຍກົງ q , ບ່ອນທີ່ 0.0 ≤ q <1.0 . ມັນສະແດງຂໍ້ມູນໃນປະຈຸບັນເປັນຊ່ວງ, ກຳ ນົດໂດຍສອງຕົວເລກ. ຄອບຄົວຂອງລະຫັດປ້ອນຂໍ້ມູນ entropy ທີ່ຜ່ານມາເອີ້ນວ່າລະບົບ ຈຳ ນວນບໍ່ເທົ່າກັນຊ່ວຍໃຫ້ມີການຈັດຕັ້ງປະຕິບັດໄດ້ໄວຂຶ້ນຍ້ອນການປະຕິບັດໂດຍກົງໃສ່ຕົວເລກ ທຳ ມະຊາດດຽວທີ່ເປັນຕົວແທນຂອງຂໍ້ມູນໃນປະຈຸບັນ
ລະຫັດເລກຄະນິດສາດ: ການຂຽນລະຫັດ Arithmetic ( AC ) ແມ່ນຮູບແບບຂອງການເຂົ້າລະຫັດແບບ entropy ທີ່ໃຊ້ໃນການບີບອັດຂໍ້ມູນທີ່ບໍ່ມີການສູນເສຍ. ໂດຍປົກກະຕິ, ສາຍອັກຂະລະຂອງຕົວລະຄອນເຊັ່ນ: ຄຳ ວ່າ "ສະບາຍດີຢູ່ທີ່ນັ້ນ" ແມ່ນຕົວແທນໂດຍໃຊ້ ຈຳ ນວນບິດຕໍ່ຕົວອັກສອນ, ຄືກັບລະຫັດ ASCII. ເມື່ອສາຍສະຕິງຖືກປ່ຽນເປັນລະບົບພາສາເລກຄະນິດສາດ, ຕົວອັກສອນທີ່ໃຊ້ເລື້ອຍໆຈະຖືກເກັບໄວ້ດ້ວຍບິດ ໜ້ອຍ ແລະຕົວອັກສອນທີ່ບໍ່ຄ່ອຍຈະເກີດຂື້ນຈະຖືກເກັບຮັກສາໄວ້ດ້ວຍກະຕ່າເພີ່ມເຕີມ, ສົ່ງຜົນໃຫ້ມີ ຈຳ ນວນນ້ອຍທີ່ໃຊ້ໃນ ຈຳ ນວນທັງ ໝົດ. ການເຂົ້າລະຫັດເລກຄະນິດສາດແຕກຕ່າງຈາກຮູບແບບອື່ນໆຂອງລະຫັດເຂົ້າລະຫັດເຊັ່ນ Huffman coding ໃນນັ້ນແທນທີ່ຈະແຍກການປ້ອນຂໍ້ມູນເຂົ້າໃນສັນຍາລັກຂອງອົງປະກອບແລະປ່ຽນແທນແຕ່ລະລະຫັດ, ການເຂົ້າລະຫັດເລກຄະນິດສາດເຂົ້າລະຫັດຂໍ້ຄວາມທັງ ໝົດ ເປັນຕົວເລກດຽວ, ສ່ວນອັດຕາສ່ວນທີ່ຖືກຕ້ອງໂດຍກົງ q , ບ່ອນທີ່ 0.0 ≤ q <1.0 . ມັນສະແດງຂໍ້ມູນໃນປະຈຸບັນເປັນຊ່ວງ, ກຳ ນົດໂດຍສອງຕົວເລກ. ຄອບຄົວຂອງລະຫັດປ້ອນຂໍ້ມູນ entropy ທີ່ຜ່ານມາເອີ້ນວ່າລະບົບ ຈຳ ນວນບໍ່ເທົ່າກັນຊ່ວຍໃຫ້ມີການຈັດຕັ້ງປະຕິບັດໄດ້ໄວຂຶ້ນຍ້ອນການປະຕິບັດໂດຍກົງໃສ່ຕົວເລກ ທຳ ມະຊາດດຽວທີ່ເປັນຕົວແທນຂອງຂໍ້ມູນໃນປະຈຸບັນ
ລະຫັດເລກຄະນິດສາດ: ການຂຽນລະຫັດ Arithmetic ( AC ) ແມ່ນຮູບແບບຂອງການເຂົ້າລະຫັດແບບ entropy ທີ່ໃຊ້ໃນການບີບອັດຂໍ້ມູນທີ່ບໍ່ມີການສູນເສຍ. ໂດຍປົກກະຕິ, ສາຍອັກຂະລະຂອງຕົວລະຄອນເຊັ່ນ: ຄຳ ວ່າ "ສະບາຍດີຢູ່ທີ່ນັ້ນ" ແມ່ນຕົວແທນໂດຍໃຊ້ ຈຳ ນວນບິດຕໍ່ຕົວອັກສອນ, ຄືກັບລະຫັດ ASCII. ເມື່ອສາຍສະຕິງຖືກປ່ຽນເປັນລະບົບພາສາເລກຄະນິດສາດ, ຕົວອັກສອນທີ່ໃຊ້ເລື້ອຍໆຈະຖືກເກັບໄວ້ດ້ວຍບິດ ໜ້ອຍ ແລະຕົວອັກສອນທີ່ບໍ່ຄ່ອຍຈະເກີດຂື້ນຈະຖືກເກັບຮັກສາໄວ້ດ້ວຍກະຕ່າເພີ່ມເຕີມ, ສົ່ງຜົນໃຫ້ມີ ຈຳ ນວນນ້ອຍທີ່ໃຊ້ໃນ ຈຳ ນວນທັງ ໝົດ. ການເຂົ້າລະຫັດເລກຄະນິດສາດແຕກຕ່າງຈາກຮູບແບບອື່ນໆຂອງລະຫັດເຂົ້າລະຫັດເຊັ່ນ Huffman coding ໃນນັ້ນແທນທີ່ຈະແຍກການປ້ອນຂໍ້ມູນເຂົ້າໃນສັນຍາລັກຂອງອົງປະກອບແລະປ່ຽນແທນແຕ່ລະລະຫັດ, ການເຂົ້າລະຫັດເລກຄະນິດສາດເຂົ້າລະຫັດຂໍ້ຄວາມທັງ ໝົດ ເປັນຕົວເລກດຽວ, ສ່ວນອັດຕາສ່ວນທີ່ຖືກຕ້ອງໂດຍກົງ q , ບ່ອນທີ່ 0.0 ≤ q <1.0 . ມັນສະແດງຂໍ້ມູນໃນປະຈຸບັນເປັນຊ່ວງ, ກຳ ນົດໂດຍສອງຕົວເລກ. ຄອບຄົວຂອງລະຫັດປ້ອນຂໍ້ມູນ entropy ທີ່ຜ່ານມາເອີ້ນວ່າລະບົບ ຈຳ ນວນບໍ່ເທົ່າກັນຊ່ວຍໃຫ້ມີການຈັດຕັ້ງປະຕິບັດໄດ້ໄວຂຶ້ນຍ້ອນການປະຕິບັດໂດຍກົງໃສ່ຕົວເລກ ທຳ ມະຊາດດຽວທີ່ເປັນຕົວແທນຂອງຂໍ້ມູນໃນປະຈຸບັນ
ເຄື່ອງປະສົມປະສານເລກຄະນິດສາດ: ໃນຄະນິດສາດ, ການ ປະສົມປະສານເລກຄະນິດສາດ ແມ່ນພາກສະ ໜາມ ທີ່ຕັດກັນຂອງທິດສະດີເລກ, ການປະສົມປະສານ, ທິດສະດີ ergodic ແລະການວິເຄາະຄວາມກົມກຽວກັນ.
ການຫັນປ່ຽນໄວສີ່ດ້ານ: ການຫັນເປັນສີ່ຫລ່ຽມໄວ ( FFT ) ແມ່ນວິທີການຄິດໄລ່ການປ່ຽນຮູບສີ່ຫລ່ຽມປ່ຽນແປງ (DFT) ທີ່ແຕກຕ່າງກັນຂອງ ລຳ ດັບ, ຫຼືການຫັນປ່ຽນທາງດ້ານ (IDFT). ການວິເຄາະຂັ້ນສີ່ປ່ຽນສັນຍານຈາກໂດເມນເດີມຂອງມັນໄປສູ່ການເປັນຕົວແທນໃນໂດເມນຄວາມຖີ່ແລະໃນທາງກັບກັນ. DFT ແມ່ນໄດ້ຮັບໂດຍການເສື່ອມໂຊມຂອງຄ່າເປັນສ່ວນປະກອບຂອງຄວາມຖີ່ທີ່ແຕກຕ່າງກັນ. ການປະຕິບັດງານນີ້ແມ່ນມີປະໂຫຍດໃນຫລາຍໆດ້ານ, ແຕ່ການຄິດໄລ່ມັນໂດຍກົງຈາກ ຄຳ ນິຍາມມັກຈະຊ້າເກີນໄປທີ່ຈະປະຕິບັດໄດ້. FFT ລວບລວມການຫັນປ່ຽນດັ່ງກ່າວຢ່າງໄວວາໂດຍການ ນຳ ປັດໃຈມາຕຣິກເບື້ອງ DFT ເຂົ້າໃນຜະລິດຕະພັນຂອງປັດໃຈກະແຈກກະຈາຍ. ດັ່ງນັ້ນ, ມັນຄຸ້ມຄອງເພື່ອຫຼຸດຜ່ອນຄວາມສັບສົນຂອງຄອມພິວເຕີ້ DFT ຈາກ , ເຊິ່ງເກີດຂື້ນຖ້າຫາກວ່າພຽງແຕ່ ນຳ ໃຊ້ ຄຳ ນິຍາມຂອງ DFT, ເຖິງ , ບ່ອນທີ່ ແມ່ນຂະ ໜາດ ຂອງຂໍ້ມູນ. ຄວາມແຕກຕ່າງຂອງຄວາມໄວສາມາດເປັນສິ່ງທີ່ໃຫຍ່ຫຼວງ, ໂດຍສະເພາະ ສຳ ລັບຊຸດຂໍ້ມູນທີ່ຍາວນານເຊິ່ງ N ອາດຈະຢູ່ໃນຫຼາຍພັນຫຼືຫຼາຍລ້ານ. ໃນທີ່ປະທັບຂອງຂໍ້ຜິດພາດຮອບ, ຫຼາຍສູດການຄິດໄລ່ FFT ແມ່ນຖືກຕ້ອງຫຼາຍກ່ວາການປະເມີນ ຄຳ ນິຍາມ DFT ໂດຍກົງຫຼືໂດຍທາງອ້ອມ. ມີຫຼາຍລະບົບການຄິດໄລ່ FFT ທີ່ແຕກຕ່າງກັນໂດຍອີງໃສ່ທິດສະດີທີ່ຖືກຈັດພີມມາຢ່າງຫຼວງຫຼາຍ, ຕັ້ງແຕ່ເລກຄະນິດສາດທີ່ສັບຊ້ອນໄປຫາທິດສະດີຂອງກຸ່ມແລະທິດສະດີເລກ.
ການຫັນປ່ຽນໄວສີ່ດ້ານ: ການຫັນເປັນສີ່ຫລ່ຽມໄວ ( FFT ) ແມ່ນວິທີການຄິດໄລ່ການປ່ຽນຮູບສີ່ຫລ່ຽມປ່ຽນແປງ (DFT) ທີ່ແຕກຕ່າງກັນຂອງ ລຳ ດັບ, ຫຼືການຫັນປ່ຽນທາງດ້ານ (IDFT). ການວິເຄາະຂັ້ນສີ່ປ່ຽນສັນຍານຈາກໂດເມນເດີມຂອງມັນໄປສູ່ການເປັນຕົວແທນໃນໂດເມນຄວາມຖີ່ແລະໃນທາງກັບກັນ. DFT ແມ່ນໄດ້ຮັບໂດຍການເສື່ອມໂຊມຂອງຄ່າເປັນສ່ວນປະກອບຂອງຄວາມຖີ່ທີ່ແຕກຕ່າງກັນ. ການປະຕິບັດງານນີ້ແມ່ນມີປະໂຫຍດໃນຫລາຍໆດ້ານ, ແຕ່ການຄິດໄລ່ມັນໂດຍກົງຈາກ ຄຳ ນິຍາມມັກຈະຊ້າເກີນໄປທີ່ຈະປະຕິບັດໄດ້. FFT ລວບລວມການຫັນປ່ຽນດັ່ງກ່າວຢ່າງໄວວາໂດຍການ ນຳ ປັດໃຈມາຕຣິກເບື້ອງ DFT ເຂົ້າໃນຜະລິດຕະພັນຂອງປັດໃຈກະແຈກກະຈາຍ. ດັ່ງນັ້ນ, ມັນຄຸ້ມຄອງເພື່ອຫຼຸດຜ່ອນຄວາມສັບສົນຂອງຄອມພິວເຕີ້ DFT ຈາກ , ເຊິ່ງເກີດຂື້ນຖ້າຫາກວ່າພຽງແຕ່ ນຳ ໃຊ້ ຄຳ ນິຍາມຂອງ DFT, ເຖິງ , ບ່ອນທີ່ ແມ່ນຂະ ໜາດ ຂອງຂໍ້ມູນ. ຄວາມແຕກຕ່າງຂອງຄວາມໄວສາມາດເປັນສິ່ງທີ່ໃຫຍ່ຫຼວງ, ໂດຍສະເພາະ ສຳ ລັບຊຸດຂໍ້ມູນທີ່ຍາວນານເຊິ່ງ N ອາດຈະຢູ່ໃນຫຼາຍພັນຫຼືຫຼາຍລ້ານ. ໃນທີ່ປະທັບຂອງຂໍ້ຜິດພາດຮອບ, ຫຼາຍສູດການຄິດໄລ່ FFT ແມ່ນຖືກຕ້ອງຫຼາຍກ່ວາການປະເມີນ ຄຳ ນິຍາມ DFT ໂດຍກົງຫຼືໂດຍທາງອ້ອມ. ມີຫຼາຍລະບົບການຄິດໄລ່ FFT ທີ່ແຕກຕ່າງກັນໂດຍອີງໃສ່ທິດສະດີທີ່ຖືກຈັດພີມມາຢ່າງຫຼວງຫຼາຍ, ຕັ້ງແຕ່ເລກຄະນິດສາດທີ່ສັບຊ້ອນໄປຫາທິດສະດີຂອງກຸ່ມແລະທິດສະດີເລກ.
ທິດສະດີTeichmüllerລະຫວ່າງສາກົນ: ທິດສະດີTeichmüllerລະຫວ່າງສາກົນ ແມ່ນຊື່ທີ່ໃຫ້ໂດຍນັກຄະນິດສາດ Shinichi Mochizuki ກັບທິດສະດີທີ່ລາວພັດທະນາໃນຊຸມປີ 2000, ປະຕິບັດຕາມວຽກກ່ອນ ໜ້າ ນັ້ນຂອງລາວໃນເລຂາຄະນິດສາດ. ອີງຕາມການ Mochizuki, ມັນແມ່ນ "ສະບັບເລກຄະນິດສາດຂອງທິດສະດີTeichmüller ສຳ ລັບທົ່ງນາເລກທີ່ຕິດກັບເສັ້ນໂຄ້ງ elliptic". ທິດສະດີດັ່ງກ່າວໄດ້ຖືກເຜີຍແຜ່ອອກສູ່ສາທາລະນະໃນຊຸດຂອງ 4 ຫົວຂໍ້ກ່ອນ ໜ້າ ນີ້ລົງໃນເວບໄຊທ໌ຂອງລາວ. ຄໍາຮ້ອງສະຫມັກທີ່ຖືກກ່າວຫາທີ່ໂດດເດັ່ນທີ່ສຸດແມ່ນການໃຫ້ຫຼັກຖານສໍາລັບຂໍ້ສະ ເໜີ ທີ່ໂດດເດັ່ນຕ່າງໆໃນທິດສະດີຈໍານວນ, ໂດຍສະເພາະແມ່ນແນວຄວາມຄິດ abc . Mochizuki ແລະນັກຄະນິດສາດອື່ນໆ ຈຳ ນວນ ໜຶ່ງ ອ້າງວ່າທິດສະດີດັ່ງກ່າວແມ່ນໄດ້ຮັບຜົນພິສູດດັ່ງກ່າວແຕ່ປັດຈຸບັນນີ້ຍັງບໍ່ທັນໄດ້ຮັບການຍອມຮັບຈາກຊຸມຊົນຄະນິດສາດ.
ຄວາມ ໜາ ແໜ້ນ ຂອງ ທຳ ມະຊາດ: ໃນທິດສະດີ ຈຳ ນວນ, ຄວາມ ໜາ ແໜ້ນ ຂອງ ທຳ ມະຊາດ ແມ່ນ ໜຶ່ງ ໃນວິທີການທີ່ຈະວັດວ່າ ຈຳ ນວນ ຈຳ ນວນທີ່ ກຳ ນົດໄວ້ຂອງ ຈຳ ນວນ ທຳ ມະຊາດແມ່ນແນວໃດ. ມັນຂື້ນກັບຄວາມເປັນໄປໄດ້ຂອງການພົບປະກັບສະມາຊິກຂອງກຸ່ມຍ່ອຍທີ່ຕ້ອງການໃນເວລາທີ່ປະສົມກັນໃນໄລຍະຫ່າງ [1, n ] ໃນຂະນະທີ່ n ເຕີບໃຫຍ່.
ອະນຸພັນກ່ຽວກັບເລກຄະນິດສາດ: ໃນທາງທິດສະດີ ໝາຍ ເລກ, Lagarias ເລກຄະນິດສາດ , ຫລື ຈຳ ນວນອະນຸພັນ ແມ່ນ ຕຳ ລາທີ່ຖືກ ກຳ ນົດ ສຳ ລັບເລກເຕັມ, ອີງໃສ່ປັດໄຈຕົ້ນຕໍ, ໂດຍການປຽບທຽບກັບກົດລະບຽບຜະລິດຕະພັນ ສຳ ລັບອະນຸພັນຂອງ ໜ້າ ທີ່ຖືກ ນຳ ໃຊ້ໃນການວິເຄາະທາງຄະນິດສາດ.
ນະໂຍບາຍດ້ານເລກຄະນິດສາດ: ນະໂຍບາຍດ້ານເລກຄະນິດສາດ ແມ່ນຂະ ແໜງ ທີ່ເຮັດໃຫ້ສອງພາກວິຊາຄະນິດສາດ, ລະບົບແບບເຄື່ອນໄຫວແລະທິດສະດີເລກ. ໃນແບບຄລາສສິກ, ນະໂຍບາຍດ້ານການຕັດສິນໃຈ ໝາຍ ເຖິງການສຶກສາຄວາມເປັນໄປໄດ້ຂອງແຜນທີ່ຕົວເອງຂອງຍົນທີ່ສັບຊ້ອນຫລືເສັ້ນຈິງ. ນະໂຍບາຍດ້ານເລກຄະນິດສາດແມ່ນການສຶກສາກ່ຽວກັບຄຸນລັກສະນະທິດສະດີເລກຂອງເລກເຕັມ, ສົມເຫດສົມຜົນ, p -adic, ແລະ / ຫຼືຈຸດກ່ຽວກັບພຶດຊະຄະນິດພາຍໃຕ້ການ ນຳ ໃຊ້ຫຼາຍ ຕຳ ແໜ່ງ ຂອງ ໜ້າ ທີ່ຫຼາຍໂພດຫຼືສົມເຫດສົມຜົນ. ເປົ້າ ໝາຍ ພື້ນຖານແມ່ນເພື່ອອະທິບາຍກ່ຽວກັບຄຸນສົມບັດເລກຄະນິດໃນແງ່ຂອງໂຄງສ້າງເລຂາຄະນິດ.
ລະຫັດເລກຄະນິດສາດ: ການຂຽນລະຫັດ Arithmetic ( AC ) ແມ່ນຮູບແບບຂອງການເຂົ້າລະຫັດແບບ entropy ທີ່ໃຊ້ໃນການບີບອັດຂໍ້ມູນທີ່ບໍ່ມີການສູນເສຍ. ໂດຍປົກກະຕິ, ສາຍອັກຂະລະຂອງຕົວລະຄອນເຊັ່ນ: ຄຳ ວ່າ "ສະບາຍດີຢູ່ທີ່ນັ້ນ" ແມ່ນຕົວແທນໂດຍໃຊ້ ຈຳ ນວນບິດຕໍ່ຕົວອັກສອນ, ຄືກັບລະຫັດ ASCII. ເມື່ອສາຍສະຕິງຖືກປ່ຽນເປັນລະບົບພາສາເລກຄະນິດສາດ, ຕົວອັກສອນທີ່ໃຊ້ເລື້ອຍໆຈະຖືກເກັບໄວ້ດ້ວຍບິດ ໜ້ອຍ ແລະຕົວອັກສອນທີ່ບໍ່ຄ່ອຍຈະເກີດຂື້ນຈະຖືກເກັບຮັກສາໄວ້ດ້ວຍກະຕ່າເພີ່ມເຕີມ, ສົ່ງຜົນໃຫ້ມີ ຈຳ ນວນນ້ອຍທີ່ໃຊ້ໃນ ຈຳ ນວນທັງ ໝົດ. ການເຂົ້າລະຫັດເລກຄະນິດສາດແຕກຕ່າງຈາກຮູບແບບອື່ນໆຂອງລະຫັດເຂົ້າລະຫັດເຊັ່ນ Huffman coding ໃນນັ້ນແທນທີ່ຈະແຍກການປ້ອນຂໍ້ມູນເຂົ້າໃນສັນຍາລັກຂອງອົງປະກອບແລະປ່ຽນແທນແຕ່ລະລະຫັດ, ການເຂົ້າລະຫັດເລກຄະນິດສາດເຂົ້າລະຫັດຂໍ້ຄວາມທັງ ໝົດ ເປັນຕົວເລກດຽວ, ສ່ວນອັດຕາສ່ວນທີ່ຖືກຕ້ອງໂດຍກົງ q , ບ່ອນທີ່ 0.0 ≤ q <1.0 . ມັນສະແດງຂໍ້ມູນໃນປະຈຸບັນເປັນຊ່ວງ, ກຳ ນົດໂດຍສອງຕົວເລກ. ຄອບຄົວຂອງລະຫັດປ້ອນຂໍ້ມູນ entropy ທີ່ຜ່ານມາເອີ້ນວ່າລະບົບ ຈຳ ນວນບໍ່ເທົ່າກັນຊ່ວຍໃຫ້ມີການຈັດຕັ້ງປະຕິບັດໄດ້ໄວຂຶ້ນຍ້ອນການປະຕິບັດໂດຍກົງໃສ່ຕົວເລກ ທຳ ມະຊາດດຽວທີ່ເປັນຕົວແທນຂອງຂໍ້ມູນໃນປະຈຸບັນ
ລະຫັດເລກຄະນິດສາດ: ການຂຽນລະຫັດ Arithmetic ( AC ) ແມ່ນຮູບແບບຂອງການເຂົ້າລະຫັດແບບ entropy ທີ່ໃຊ້ໃນການບີບອັດຂໍ້ມູນທີ່ບໍ່ມີການສູນເສຍ. ໂດຍປົກກະຕິ, ສາຍອັກຂະລະຂອງຕົວລະຄອນເຊັ່ນ: ຄຳ ວ່າ "ສະບາຍດີຢູ່ທີ່ນັ້ນ" ແມ່ນຕົວແທນໂດຍໃຊ້ ຈຳ ນວນບິດຕໍ່ຕົວອັກສອນ, ຄືກັບລະຫັດ ASCII. ເມື່ອສາຍສະຕິງຖືກປ່ຽນເປັນລະບົບພາສາເລກຄະນິດສາດ, ຕົວອັກສອນທີ່ໃຊ້ເລື້ອຍໆຈະຖືກເກັບໄວ້ດ້ວຍບິດ ໜ້ອຍ ແລະຕົວອັກສອນທີ່ບໍ່ຄ່ອຍຈະເກີດຂື້ນຈະຖືກເກັບຮັກສາໄວ້ດ້ວຍກະຕ່າເພີ່ມເຕີມ, ສົ່ງຜົນໃຫ້ມີ ຈຳ ນວນນ້ອຍທີ່ໃຊ້ໃນ ຈຳ ນວນທັງ ໝົດ. ການເຂົ້າລະຫັດເລກຄະນິດສາດແຕກຕ່າງຈາກຮູບແບບອື່ນໆຂອງລະຫັດເຂົ້າລະຫັດເຊັ່ນ Huffman coding ໃນນັ້ນແທນທີ່ຈະແຍກການປ້ອນຂໍ້ມູນເຂົ້າໃນສັນຍາລັກຂອງອົງປະກອບແລະປ່ຽນແທນແຕ່ລະລະຫັດ, ການເຂົ້າລະຫັດເລກຄະນິດສາດເຂົ້າລະຫັດຂໍ້ຄວາມທັງ ໝົດ ເປັນຕົວເລກດຽວ, ສ່ວນອັດຕາສ່ວນທີ່ຖືກຕ້ອງໂດຍກົງ q , ບ່ອນທີ່ 0.0 ≤ q <1.0 . ມັນສະແດງຂໍ້ມູນໃນປະຈຸບັນເປັນຊ່ວງ, ກຳ ນົດໂດຍສອງຕົວເລກ. ຄອບຄົວຂອງລະຫັດປ້ອນຂໍ້ມູນ entropy ທີ່ຜ່ານມາເອີ້ນວ່າລະບົບ ຈຳ ນວນບໍ່ເທົ່າກັນຊ່ວຍໃຫ້ມີການຈັດຕັ້ງປະຕິບັດໄດ້ໄວຂຶ້ນຍ້ອນການປະຕິບັດໂດຍກົງໃສ່ຕົວເລກ ທຳ ມະຊາດດຽວທີ່ເປັນຕົວແທນຂອງຂໍ້ມູນໃນປະຈຸບັນ
ການສະແດງອອກ (ຄະນິດສາດ): ໃນຄະນິດສາດ, ສຳ ນວນ ຫລື ສຳ ນວນ ທາງຄະນິດສາດ ແມ່ນການປະສົມປະສານລະອຽດຂອງສັນຍາລັກທີ່ຖືກຈັດຕັ້ງຂື້ນເປັນລະບຽບຕາມກົດເກນທີ່ຂື້ນກັບສະພາບການ ສັນຍາລັກທາງຄະນິດສາດສາມາດອອກແບບຕົວເລກ (ຄົງທີ່), ຕົວແປ, ການ ດຳ ເນີນງານ, ໜ້າ ທີ່, ວົງເລັບ, ເຄື່ອງ ໝາຍ ວັກແລະການຈັດກຸ່ມເພື່ອຊ່ວຍ ກຳ ນົດ ຄຳ ສັ່ງຂອງການ ດຳ ເນີນງານ, ແລະລັກສະນະອື່ນໆຂອງ syntax ທີ່ມີເຫດຜົນ.
ເລກຄະນິດສາດ ສຳ ລັບພໍ່ແມ່: ເລກຄະນິດສາດ ສຳ ລັບພໍ່ແມ່ ແມ່ນປື້ມກ່ຽວກັບການສຶກສາດ້ານຄະນິດສາດແນໃສ່ພໍ່ແມ່ແລະຄູ.
ເລກຄະນິດສາດ ສຳ ລັບພໍ່ແມ່: ເລກຄະນິດສາດ ສຳ ລັບພໍ່ແມ່ ແມ່ນປື້ມກ່ຽວກັບການສຶກສາດ້ານຄະນິດສາດແນໃສ່ພໍ່ແມ່ແລະຄູ.
axioms Peano: ໃນທາງເລກຄະນິດສາດ, Peano axioms , ເຊິ່ງເອີ້ນກັນວ່າ Dedekind – Peano axioms ຫຼື the Peano postulates , ແມ່ນຕົວເລກ ສຳ ລັບຕົວເລກ ທຳ ມະຊາດທີ່ ນຳ ສະ ເໜີ ໂດຍນັກຄະນິດສາດອິຕາລີ Giuseppe Peano. ບັນດາເອກະສານເຫຼົ່ານີ້ໄດ້ຖືກ ນຳ ໃຊ້ເກືອບບໍ່ປ່ຽນແປງໃນການຄົ້ນຄວ້າວິເຄາະທາງດ້ານວິຊາເລກ, ລວມທັງການຄົ້ນຄ້ວາ ຄຳ ຖາມພື້ນຖານກ່ຽວກັບວ່າທິດສະດີຂອງຕົວເລກແມ່ນສອດຄ່ອງແລະຄົບຖ້ວນຫຼືບໍ່.
ແຕ່ສ່ວນຫນຶ່ງ: ສ່ວນ ໜຶ່ງ ສ່ວນ ໜຶ່ງ ສະ ແດງໃຫ້ເຫັນສ່ວນ ໜຶ່ງ ຂອງສ່ວນ ໜຶ່ງ ຫຼືໂດຍທົ່ວໄປ, ສ່ວນໃດສ່ວນ ໜຶ່ງ ເທົ່າກັນ. ເມື່ອເວົ້າໃນພາສາອັງກິດປະ ຈຳ ວັນ, ສ່ວນ ໜຶ່ງ ຈະອະທິບາຍເຖິງສ່ວນໃດສ່ວນ ໜຶ່ງ ຂອງຂະ ໜາດ ທີ່ແນ່ນອນ, ຕົວຢ່າງ, ເຄິ່ງ ໜຶ່ງ, ແປດ, ຫ້າ, ສາມສ່ວນສີ່. A ທົ່ວໄປ, vulgar, ຫຼືສ່ວນຫນຶ່ງງ່າຍດາຍປະກອບດ້ວຍຈໍານວນຫລາຍເປັນການສະແດງຂ້າງເທິງນີ້ບັນທັດລະແລະບໍ່ມີການສູນຫານ, ສະແດງຂ້າງລຸ່ມນີ້ເສັ້ນນັ້ນ. ເຄື່ອງນັບແລະຕົວຫານຍັງຖືກ ນຳ ໃຊ້ໃນສ່ວນປະກອບທີ່ບໍ່ ທຳ ມະດາ , ລວມທັງສ່ວນປະສົມ, ສ່ວນສະລັບສັບຊ້ອນແລະຕົວເລກປະສົມ.
ການ ທຳ ງານຂອງເລກຄະນິດສາດ: ໃນທິດສະດີ ຈຳ ນວນ, ຕຳ ລາ ຄະນິດສາດ , ເລກຄະນິດສາດ ຫລື ຈຳ ນວນທິດສະດີ ແມ່ນ ສຳ ລັບຜູ້ຂຽນສ່ວນຫຼາຍແມ່ນ ຕຳ ແໜ່ງ f ( n ) ທີ່ໂດເມນແມ່ນເລກບວກແລະ ຈຳ ນວນຂອງມັນແມ່ນ ຈຳ ນວນຍ່ອຍຂອງຕົວເລກທີ່ສັບສົນ. Hardy & Wright ປະກອບມີໃນນິຍາມຂອງພວກເຂົາຄວາມຕ້ອງການທີ່ວ່າ ໜ້າ ທີ່ກ່ຽວກັບເລກ "ສະແດງຄຸນສົມບັດເລກຄະນິດສາດຂອງ n ".
ການ ທຳ ງານຂອງເລກຄະນິດສາດ: ໃນທິດສະດີ ຈຳ ນວນ, ຕຳ ລາ ຄະນິດສາດ , ເລກຄະນິດສາດ ຫລື ຈຳ ນວນທິດສະດີ ແມ່ນ ສຳ ລັບຜູ້ຂຽນສ່ວນຫຼາຍແມ່ນ ຕຳ ແໜ່ງ f ( n ) ທີ່ໂດເມນແມ່ນເລກບວກແລະ ຈຳ ນວນຂອງມັນແມ່ນ ຈຳ ນວນຍ່ອຍຂອງຕົວເລກທີ່ສັບສົນ. Hardy & Wright ປະກອບມີໃນນິຍາມຂອງພວກເຂົາຄວາມຕ້ອງການທີ່ວ່າ ໜ້າ ທີ່ກ່ຽວກັບເລກ "ສະແດງຄຸນສົມບັດເລກຄະນິດສາດຂອງ n ".
ສະກຸນເລກຄະນິດສາດ: ໃນວິຊາຄະນິດສາດ, ສະ ກຸນເລກຄະນິດສາດ ຂອງແນວພັນພຶດຊະຄະນິດແມ່ນ ໜຶ່ງ ໃນສອງສາມຕົວຢ່າງທີ່ເປັນໄປໄດ້ຂອງສະກຸນຂອງເສັ້ນໂຄ້ງຂອງພຶດຊະຄະນິດຫຼືດ້ານ Riemann.
ເລກຄະນິດສາດ - ເລຂາຄະນິດ: ໃນຄະນິດສາດ, ເລກຄະນິດສາດ – ເລຂາຄະນິດ ຂອງສອງຕົວເລກຕົວບວກ x ແລະ y ແມ່ນ ກຳ ນົດດັ່ງຕໍ່ໄປນີ້:
ເລຂາຄະນິດກ່ຽວກັບເລກຄະນິດສາດ: ໃນຄະນິດສາດ, ເລຂາຄະນິດສາດ ແມ່ນປະມານການ ນຳ ໃຊ້ເຕັກນິກຈາກເລຂາຄະນິດຄະນິດສາດເຖິງບັນຫາໃນທິດສະດີເລກ. ເລຂາຄະນິດກ່ຽວກັບເລກຄະນິດສາດແມ່ນເປັນຈຸດສູນກາງປະມານເລຂາຄະນິດ Diophantine, ການສຶກສາຈຸດທີ່ສົມເຫດສົມຜົນຂອງແນວພັນພຶດຊະຄະນິດ.
ກຸ່ມເລກຄະນິດສາດ: ໃນຄະນິດສາດ, ກຸ່ມເລກຄະນິດສາດ ແມ່ນກຸ່ມ ໜຶ່ງ ທີ່ໄດ້ຮັບເປັນຈຸດບວກຂອງກຸ່ມພຶດຊະຄະນິດ, ຕົວຢ່າງ ພວກມັນເກີດຂື້ນຕາມ ທຳ ມະຊາດໃນການສຶກສາກ່ຽວກັບຄຸນສົມບັດເລກຄະນິດຂອງຮູບແບບສີ່ຫລ່ຽມແລະຫົວຂໍ້ຄລາສສິກອື່ນໆໃນທິດສະດີເລກ. ພວກເຂົາຍັງໃຫ້ຕົວຢ່າງທີ່ຫນ້າສົນໃຈຫຼາຍກ່ຽວກັບ manifolds Riemannian ແລະເພາະສະນັ້ນຈຶ່ງແມ່ນວັດຖຸທີ່ສົນໃຈກ່ຽວກັບເລຂາຄະນິດແລະ topology. ສຸດທ້າຍ, ສອງຫົວຂໍ້ນີ້ເຂົ້າຮ່ວມໃນທິດສະດີຂອງຮູບແບບອັດຕະໂນມັດເຊິ່ງເປັນພື້ນຖານໃນທິດສະດີເລກທັນສະ ໄໝ.
ໜ້າ ທີ່ເສັ້ນ: ໃນຄະນິດສາດ, ຄຳ ວ່າ linear function ໝາຍ ເຖິງສອງແນວຄິດທີ່ແຕກຕ່າງກັນແຕ່ກ່ຽວຂ້ອງ: ໃນການຄິດໄລ່ແລະພື້ນທີ່ທີ່ກ່ຽວຂ້ອງ, ໜ້າ ທີ່ເປັນເສັ້ນແມ່ນ ໜ້າ ທີ່ເສັ້ນສະແດງເປັນເສັ້ນຊື່, ນັ້ນແມ່ນ ຕຳ ລາ polynomial ຂອງລະດັບສູນຫຼື ໜຶ່ງ. ສຳ ລັບການ ຈຳ ແນກ ຕຳ ແໜ່ງ ເສັ້ນຊື່ດັ່ງກ່າວຈາກແນວຄິດອື່ນໆ, ຄຳ ວ່າ ຕຳ ແໜ່ງ ທີ່ມີຄວາມ ໝາຍ ມັກຈະຖືກ ນຳ ໃຊ້ເລື້ອຍໆ. ໃນພຶດຊະຄະນິດເສັ້ນ, ການວິເຄາະທາງຄະນິດສາດ, ແລະການວິເຄາະທີ່ເປັນປະໂຫຍດ, ໜ້າ ທີ່ເປັນເສັ້ນແມ່ນແຜນທີ່ເສັ້ນຊື່.
ເລຂາຄະນິດ ໝາຍ ເລກ: ໃນຄະນິດສາດ, ວິຊາ ເລຂາຄະນິດ ແມ່ນຕົວເລກຫຼືສະເລ່ຍ, ເຊິ່ງສະແດງເຖິງທ່າອ່ຽງໃຈກາງຫຼືມູນຄ່າປົກກະຕິຂອງຕົວເລກທີ່ ກຳ ນົດໄວ້ໂດຍການ ນຳ ໃຊ້ຜະລິດຕະພັນຂອງຄຸນຄ່າຂອງພວກເຂົາ. ສະເລ່ຍ geometric ຖືກກໍານົດເປັນ n th root ຜະລິດຕະພັນຂອງຕົວເລກ n, ຕົວຢ່າງ, ສໍາລັບການທີ່ກໍານົດໄວ້ຂອງຕົວເລກ x 1, x 2, ... , x n, ສະເລ່ຍ geometric ແມ່ນກໍານົດເປັນ
ລຳ ດັບຊັ້ນເລກຄະນິດສາດ: ໃນຄວາມ ໝາຍ ທາງຄະນິດສາດ, ລຳ ດັບຊັ້ນຄະນິດສາດ , ລຳ ດັບຊັ້ນ ເລກຄະນິດສາດ ຫຼື ລຳ ດັບຊັ້ນສູງ Kleene – Mostowski ແມ່ນ ກຳ ນົດບາງຊຸດໂດຍອີງໃສ່ຄວາມສັບສົນຂອງສູດທີ່ ກຳ ນົດພວກມັນ. ຊຸດໃດກໍ່ຕາມທີ່ໄດ້ຮັບການຈັດປະເພດແມ່ນຖືກເອີ້ນວ່າ ເລກຄະນິດສາດ .
ຕຶກອາຄານ hyperbolic 3-manifold: ໃນຄະນິດສາດ, ມີຄວາມຊັດເຈນກວ່າໃນທິດສະດີກຸ່ມແລະເລຂາຄະນິດ hyperbolic, ກຸ່ມ Arithmetic Kleinian ແມ່ນຊັ້ນຮຽນພິເສດຂອງກຸ່ມ Kleinian ທີ່ສ້າງໂດຍໃຊ້ ຄຳ ສັ່ງໃນ alaterbras quaternion. ພວກເຂົາແມ່ນຕົວຢ່າງໂດຍສະເພາະຂອງກຸ່ມເລກຄະນິດສາດ. ຕົວຊີ້ວັດ hyperbolic ສາມແບບ ເປັນຕົວເລກຂອງ ຈຳ ນວນອະວະກາດ hyperbolic ໂດຍກຸ່ມ Kleinian ເລກຄະນິດສາດ. manifold ເຫຼົ່ານີ້ປະກອບມີຕົວຢ່າງທີ່ສວຍງາມໂດຍສະເພາະບາງຢ່າງ.
ກຸ່ມ Arithmetic Fuchsian: ກຸ່ມ Arithmetic Fuchsian ແມ່ນຊັ້ນຮຽນພິເສດຂອງກຸ່ມ Fuchsian ທີ່ສ້າງໂດຍໃຊ້ ຄຳ ສັ່ງໃນ alaterbras quaternion. ພວກເຂົາແມ່ນຕົວຢ່າງໂດຍສະເພາະຂອງກຸ່ມເລກຄະນິດສາດ. ຕົວຢ່າງຕົ້ນແບບຂອງກຸ່ມ Fuchsian ກ່ຽວກັບເລກຄະນິດສາດແມ່ນກຸ່ມແບບໂມດູນ . ພວກເຂົາ, ແລະພື້ນຜິວ hyperbolic ທີ່ກ່ຽວຂ້ອງກັບການປະຕິບັດງານຂອງພວກເຂົາໃນຍົນ hyperbolic ມັກຈະສະແດງພຶດຕິ ກຳ ທີ່ເປັນປົກກະຕິໂດຍສະເພາະໃນກຸ່ມ Fuchsian ແລະ ໜ້າ hyperbolic.
ເລກຄະນິດສາດ IF: ຄຳ ຖະແຫຼງ ກ່ຽວກັບເລກຄະນິດສາດ IF ແມ່ນ ຄຳ ຖະແຫຼງເງື່ອນໄຂກ່ຽວກັບເລກຄະນິດສາດ, ເຊິ່ງເຫັນໄດ້ໃນການປ່ອຍ Fortran ຄັ້ງ ທຳ ອິດໃນປີ 1957, ແລະພົບໃນທຸກລຸ້ນຕໍ່ມາ, ແລະບາງພາສາການຂຽນໂປຼແກຼມອື່ນໆ, ເຊັ່ນ FOCAL. ບໍ່ຄືກັບ ຄຳ ເວົ້າ IF ຢ່າງມີເຫດຜົນທີ່ເຫັນໃນພາສາອື່ນໆ, ຄຳ ຖະແຫຼງທີ່ Fortran ກຳ ນົດສາມສາຂາທີ່ແຕກຕ່າງກັນຂື້ນຢູ່ກັບວ່າຜົນຂອງການສະແດງອອກແມ່ນລົບ, ສູນ, ຫລືບວກ, ໃນ ຄຳ ສັ່ງທີ່ກ່າວໄວ້, ຂຽນເປັນ:
ບົດເກົ້າບົດກ່ຽວກັບສິນລະປະຄະນິດສາດ: ບົດເກົ້າບົດກ່ຽວກັບຄະນິດສາດ ແມ່ນປື້ມປື້ມຄະນິດສາດຂອງຈີນ, ປະກອບດ້ວຍນັກວິທະຍາກອນລຸ້ນສືບທອດມາແຕ່ສະຕະວັດທີ 10 - 2 ສະຕະວັດທີ 2, ເຊິ່ງຂັ້ນຕອນສຸດທ້າຍຂອງມັນແມ່ນມາຈາກສະຕະວັດທີ 2 ສະຕະວັດ. ປື້ມຫົວນີ້ແມ່ນ ໜຶ່ງ ໃນບັນດາຕົວ ໜັງ ສືຄະນິດສາດທີ່ມີຊີວິດລອດທີ່ສຸດຈາກປະເທດຈີນ, ປື້ມ ທຳ ອິດແມ່ນ Suan shu shu ແລະ Zhoubi Suanjing . ມັນວາງອອກວິທີການກ່ຽວກັບຄະນິດສາດເຊິ່ງເປັນສູນກາງໃນການຊອກຫາວິທີການແກ້ໄຂບັນຫາທົ່ວໄປທີ່ສຸດ, ເຊິ່ງມັນອາດຈະກົງກັນຂ້າມກັບວິທີການທົ່ວໄປຂອງນັກຄະນິດສາດຊາວເກຣັກບູຮານ, ຜູ້ທີ່ມີແນວໂນ້ມທີ່ຈະຄິດໄລ່ຂໍ້ສະ ເໜີ ຕ່າງໆຈາກຊຸດເລີ່ມຕົ້ນຂອງ axioms.
ເລກຄະນິດສາດພາກສະ ໜາມ: ໃນຄະນິດສາດ, ເລກຄະນິດສາດພາກສະ ໜາມ ແມ່ນເລກຄະນິດສາດໃນພາກສະ ໜາມ ທີ່ ຈຳ ກັດກົງກັນຂ້າມກັບເລກຄະນິດສາດໃນສະ ໜາມ ທີ່ມີ ຈຳ ນວນອົງປະກອບທີ່ບໍ່ມີຂອບເຂດ, ຄືພາກສະ ໜາມ ຂອງຕົວເລກສົມເຫດສົມຜົນ.
ບົດເກົ້າບົດກ່ຽວກັບສິນລະປະຄະນິດສາດ: ບົດເກົ້າບົດກ່ຽວກັບຄະນິດສາດ ແມ່ນປື້ມປື້ມຄະນິດສາດຂອງຈີນ, ປະກອບດ້ວຍນັກວິທະຍາກອນລຸ້ນສືບທອດມາແຕ່ສະຕະວັດທີ 10 - 2 ສະຕະວັດທີ 2, ເຊິ່ງຂັ້ນຕອນສຸດທ້າຍຂອງມັນແມ່ນມາຈາກສະຕະວັດທີ 2 ສະຕະວັດ. ປື້ມຫົວນີ້ແມ່ນ ໜຶ່ງ ໃນບັນດາຕົວ ໜັງ ສືຄະນິດສາດທີ່ມີຊີວິດລອດທີ່ສຸດຈາກປະເທດຈີນ, ປື້ມ ທຳ ອິດແມ່ນ Suan shu shu ແລະ Zhoubi Suanjing . ມັນວາງອອກວິທີການກ່ຽວກັບຄະນິດສາດເຊິ່ງເປັນສູນກາງໃນການຊອກຫາວິທີການແກ້ໄຂບັນຫາທົ່ວໄປທີ່ສຸດ, ເຊິ່ງມັນອາດຈະກົງກັນຂ້າມກັບວິທີການທົ່ວໄປຂອງນັກຄະນິດສາດຊາວເກຣັກບູຮານ, ຜູ້ທີ່ມີແນວໂນ້ມທີ່ຈະຄິດໄລ່ຂໍ້ສະ ເໜີ ຕ່າງໆຈາກຊຸດເລີ່ມຕົ້ນຂອງ axioms.
ຮູບແບບມຸງ: ຮູບແບບ Roofline ແມ່ນ ຮູບແບບ ການປະຕິບັດການເບິ່ງເຫັນທີ່ໃຊ້ໄດ້ໂດຍໃຊ້ໃນການຄາດຄະເນການປະຕິບັດງານຂອງ kernel ຄອມພິວເຕີ້ທີ່ມີໃຫ້ຫຼືການ ນຳ ໃຊ້ທີ່ເຮັດວຽກກ່ຽວກັບສະຖາປັດຕະຍະ ກຳ ທີ່ມີຫຼາຍແກນ, ຫຼາຍແກນ, ຫຼືເລັ່ງລັດ, ໂດຍການສະແດງຂໍ້ ຈຳ ກັດດ້ານຮາດແວທີ່ປະກົດຂຶ້ນ, ແລະຜົນປະໂຫຍດທີ່ເປັນໄປໄດ້ແລະຄວາມ ສຳ ຄັນຂອງການເພີ່ມປະສິດທິພາບ ໂດຍການສົມທົບທ້ອງຖິ່ນ, ແບນວິດແລະຕົວແບບຂະຫນານທີ່ແຕກຕ່າງກັນເຂົ້າໄປໃນຕົວເລກການປະຕິບັດດຽວ, ຮູບແບບສາມາດເປັນທາງເລືອກທີ່ມີປະສິດຕິພາບໃນການປະເມີນຄຸນະພາບຂອງການປະຕິບັດທີ່ບັນລຸໄດ້ແທນທີ່ຈະໃຊ້ການຄາດຄະເນເປີເຊັນຂອງຈຸດສູງສຸດ, ຍ້ອນວ່າມັນສະ ໜອງ ຄວາມເຂົ້າໃຈກ່ຽວກັບການຈັດຕັ້ງປະຕິບັດແລະ ຂໍ້ ຈຳ ກັດດ້ານການປະຕິບັດທີ່ປະກົດຂຶ້ນ.
ກັນຫລາຍດ້ານ: ໃນຄະນິດສາດ, ເປັນກົງກັນຂ້າມ multiplicative ຫລືຊຶ່ງກັນແລະກັນສໍາລັບການຈໍານວນ x, ສະແດງດ້ວຍ 1 / x ຫຼື x -1, ເປັນຈໍານວນທີ່ໃນເວລາທີ່ຄູນ x yields ເຖິງເອກະລັກ multiplicative, 1. ການກັນ multiplicative ຂອງແຕ່ສ່ວນຫນຶ່ງ a / b ແມ່ນ b / ກ . ສຳ ລັບການຄູນທະວີຄູນຂອງ ຈຳ ນວນທີ່ແທ້ຈິງ, ແບ່ງ 1 ຕາມ ຈຳ ນວນ. ຍົກຕົວຢ່າງ, ທາງກັບກັນຂອງ 5 ແມ່ນ ໜຶ່ງ ສ່ວນຫ້າ, ແລະຕ່າງຝ່າຍຕ່າງຂອງ 0.25 ແມ່ນ 1 ແບ່ງເປັນ 0.25, ຫຼື 4. ຕຳ ແໜ່ງ ຕ່າງຝ່າຍຕ່າງ , ໜ້າ ທີ່ f ( x ) ທີ່ມີແຜນທີ່ x ເຖິງ 1 / x , ແມ່ນຕົວຢ່າງ ໜຶ່ງ ທີ່ງ່າຍດາຍທີ່ສຸດຂອງ ໜ້າ ທີ່ເຊິ່ງມັນແມ່ນປີ້ນກັບກັນຂອງຕົວເອງ.
ເສັ້ນລວດ (ແຍກກຸ່ມຍ່ອຍ): ໃນທິດສະດີ Lie ແລະພື້ນທີ່ກ່ຽວຂ້ອງຂອງຄະນິດສາດ, ເສັ້ນ ລ້ອນ ໃນກຸ່ມທີ່ມີຄວາມ ແໜ້ນ ໜາ ຢູ່ໃນທ້ອງຖິ່ນແມ່ນກຸ່ມຍ່ອຍທີ່ມີຄຸນສົມບັດທີ່ພື້ນທີ່ ຈຳ ນວນ ໜຶ່ງ ມີມາດຕະການທີ່ບໍ່ມີຕົວຕົນ. ໃນກໍລະນີພິເສດຂອງກຸ່ມຍ່ອຍຂອງ R n , ປະລິມານນີ້ແມ່ນມີຄວາມ ໝາຍ ທາງເລຂາຄະນິດຕາມປົກກະຕິຂອງເສັ້ນລ້ອນເປັນຈຸດຍ່ອຍຕາມແຕ່ລະໄລຍະ, ແລະທັງໂຄງສ້າງເພັງຂອງຄະນິດສາດແລະເລຂາຄະນິດຂອງພື້ນທີ່ຂອງທ່ອນທັງ ໝົດ ແມ່ນຂ້ອນຂ້າງເຂົ້າໃຈດີ.
ເສັ້ນເລືອດສະຫມອງ: Dyscalculia ແມ່ນຄວາມພິການທີ່ເຮັດໃຫ້ເກີດຄວາມຫຍຸ້ງຍາກໃນການຮຽນຮູ້ຫຼືເຂົ້າໃຈກ່ຽວກັບເລກຄະນິດສາດເຊັ່ນ: ຄວາມຫຍຸ້ງຍາກໃນການເຂົ້າໃຈຕົວເລກ, ຮຽນຮູ້ການ ໝູນ ໃຊ້ຕົວເລກ, ປະຕິບັດການຄິດໄລ່ທາງຄະນິດສາດແລະການຮຽນຮູ້ຂໍ້ມູນທາງຄະນິດສາດ. ບາງຄັ້ງມັນຖືກເອີ້ນວ່າບໍ່ເປັນທາງການເປັນ "dyslexia ເລກ", ເຖິງແມ່ນວ່າສິ່ງນີ້ສາມາດຫຼອກລວງໄດ້ຍ້ອນວ່າ dyslexia ແມ່ນສະພາບທີ່ແຕກຕ່າງຈາກ dyscalculia.
ການປ່ຽນແປງເລກຄະນິດສາດ: ໃນການຂຽນໂປແກຼມຄອມພິວເຕີ້, ການ ປ່ຽນເລກຄະນິດສາດ ແມ່ນຜູ້ປະຕິບັດການປ່ຽນແປງ, ບາງຄັ້ງກໍ່ເອີ້ນວ່າການ ປ່ຽນແປງທີ່ເຊັນ . ສອງປະເພດພື້ນຖານແມ່ນການ ເລື່ອນຊ້າຍດ້ານເລກເລກ ແລະການ ເລື່ອນຂວາດ້ານເລກເລກ . ສຳ ລັບຕົວເລກຖານສອງມັນແມ່ນການ ດຳ ເນີນງານທີ່ມີຄວາມ ໝາຍ ເລັກນ້ອຍທີ່ປ່ຽນສ່ວນທັງ ໝົດ ຂອງ ລຳ ດັບຂອງມັນ; ທຸກໆບິດໃນລະຄອນພຽງແຕ່ຍ້າຍ ຈຳ ນວນ ຕຳ ແໜ່ງ ນ້ອຍໆ, ແລະ ຕຳ ແໜ່ງ bit-vacant ທີ່ເຕັມໄປດ້ວຍ. ແທນທີ່ຈະເຕັມໄປດ້ວຍ 0s ທັງ ໝົດ, ຄືກັບການປ່ຽນທິດທາງທີ່ສົມເຫດສົມຜົນ, ເມື່ອປ່ຽນໄປທາງຂວາ, ສ່ວນທາງຊ້າຍແມ່ນຖືກປ່ຽນແທນ ຕື່ມທຸກ ຕຳ ແໜ່ງ ທີ່ວ່າງ.
ໜ່ວຍ ງານຕາມເຫດຜົນເລກຄະນິດສາດ: ໃນການຄິດໄລ່ຄອມພິວເຕີ້, ໜ່ວຍ ງານຕາມເຫດຜົນກ່ຽວກັບເລກຄະນິດສາດ (ALU) ແມ່ນວົງຈອນດິຈິຕອນປະສົມປະສານທີ່ເຮັດ ໜ້າ ທີ່ກ່ຽວກັບເລກຄະນິດສາດແລະຂີດຕໍ່ເລກຖານສອງ. ນີ້ແມ່ນກົງກັນຂ້າມກັບຫົວ ໜ່ວຍ ຈຸດທີ່ລອຍຕົວ (FPU), ເຊິ່ງ ດຳ ເນີນງານກ່ຽວກັບຕົວເລກຈຸດລອຍ. ມັນແມ່ນສິ່ງກໍ່ສ້າງພື້ນຖານຂອງວົງຈອນຄອມພິວເຕີ້ຫລາຍປະເພດ, ລວມທັງ ໜ່ວຍ ງານປະມວນຜົນສູນກາງ (CPU) ຂອງຄອມພິວເຕີ້, FPUs, ແລະ ໜ່ວຍ ປະມວນຜົນກາຟິກ (GPUs).
ໜ່ວຍ ງານຕາມເຫດຜົນເລກຄະນິດສາດ: ໃນການຄິດໄລ່ຄອມພິວເຕີ້, ໜ່ວຍ ງານຕາມເຫດຜົນກ່ຽວກັບເລກຄະນິດສາດ (ALU) ແມ່ນວົງຈອນດິຈິຕອນປະສົມປະສານທີ່ເຮັດ ໜ້າ ທີ່ກ່ຽວກັບເລກຄະນິດສາດແລະຂີດຕໍ່ເລກຖານສອງ. ນີ້ແມ່ນກົງກັນຂ້າມກັບຫົວ ໜ່ວຍ ຈຸດທີ່ລອຍຕົວ (FPU), ເຊິ່ງ ດຳ ເນີນງານກ່ຽວກັບຕົວເລກຈຸດລອຍ. ມັນແມ່ນສິ່ງກໍ່ສ້າງພື້ນຖານຂອງວົງຈອນຄອມພິວເຕີ້ຫລາຍປະເພດ, ລວມທັງ ໜ່ວຍ ງານປະມວນຜົນສູນກາງ (CPU) ຂອງຄອມພິວເຕີ້, FPUs, ແລະ ໜ່ວຍ ປະມວນຜົນກາຟິກ (GPUs).
ໜ່ວຍ ງານຕາມເຫດຜົນເລກຄະນິດສາດ: ໃນການຄິດໄລ່ຄອມພິວເຕີ້, ໜ່ວຍ ງານຕາມເຫດຜົນກ່ຽວກັບເລກຄະນິດສາດ (ALU) ແມ່ນວົງຈອນດິຈິຕອນປະສົມປະສານທີ່ເຮັດ ໜ້າ ທີ່ກ່ຽວກັບເລກຄະນິດສາດແລະຂີດຕໍ່ເລກຖານສອງ. ນີ້ແມ່ນກົງກັນຂ້າມກັບຫົວ ໜ່ວຍ ຈຸດທີ່ລອຍຕົວ (FPU), ເຊິ່ງ ດຳ ເນີນງານກ່ຽວກັບຕົວເລກຈຸດລອຍ. ມັນແມ່ນສິ່ງກໍ່ສ້າງພື້ນຖານຂອງວົງຈອນຄອມພິວເຕີ້ຫລາຍປະເພດ, ລວມທັງ ໜ່ວຍ ງານປະມວນຜົນສູນກາງ (CPU) ຂອງຄອມພິວເຕີ້, FPUs, ແລະ ໜ່ວຍ ປະມວນຜົນກາຟິກ (GPUs).
ເຄື່ອງຄິດໄລ່ຂອງ Pascal: ເຄື່ອງຄິດໄລ່ຂອງ Pascal ແມ່ນເຄື່ອງຄິດໄລ່ກົນຈັກທີ່ຖືກສ້າງຂື້ນໂດຍ Blaise Pascal ໃນກາງສະຕະວັດທີ 17. Pascal ຖືກ ນຳ ພາໃຫ້ພັດທະນາເຄື່ອງຄິດໄລ່ໂດຍການ ຄຳ ນວນເລກຄະນິດສາດທີ່ໃຊ້ແຮງງານທີ່ພໍ່ຂອງລາວເປັນຜູ້ຄວບຄຸມພາສີໃນ Rouen. ລາວໄດ້ອອກແບບເຄື່ອງເພື່ອເພີ່ມແລະຫັກອອກສອງຕົວເລກໂດຍກົງແລະເພື່ອປະຕິບັດການຄູນແລະການແບ່ງໂດຍການເພີ່ມຫຼືການຫັກລົບອີກເທື່ອ ໜຶ່ງ.
ເລກຄະນິດສາດ: ໃນຄະນິດສາດແລະສະຖິຕິ, ຄວາມ ໝາຍ ເລກຄະນິດສາດ , ຫຼືພຽງແຕ່ຄ່າສະເລ່ຍຫຼື ສະເລ່ຍ , ແມ່ນການລວມຕົວເລກຂອງຕົວເລກທີ່ແບ່ງຕາມການນັບຂອງຕົວເລກໃນການເກັບ. ການລວບລວມມັກຈະເປັນຊຸດຂອງຜົນຂອງການທົດລອງຫຼືການສຶກສາການສັງເກດການ, ຫຼືມັກຈະເປັນຊຸດຂອງຜົນໄດ້ຮັບຈາກການ ສຳ ຫຼວດ. ຄຳ ວ່າ "ຄວາມ ໝາຍ ເລກຄະນິດສາດ" ແມ່ນມັກໃນບາງສະພາບການໃນຄະນິດສາດແລະສະຖິຕິ, ເພາະວ່າມັນຊ່ວຍແຍກແຍະມັນຈາກວິທີອື່ນ, ເຊັ່ນ: ຄວາມ ໝາຍ ຂອງເລຂາຄະນິດແລະຄວາມ ໝາຍ ທີ່ມີຄວາມ ໝາຍ.
ຄວາມບໍ່ສະເຫມີພາບຂອງເລກຄະນິດສາດແລະເລຂາຄະນິດ: ໃນທາງຄະນິດສາດ, ຄວາມບໍ່ສະ ເໝີ ພາບຂອງວິທີເລກຄະນິດສາດແລະເລຂາຄະນິດ , ຫຼືເວົ້າສັ້ນໆກວ່າ ຄວາມບໍ່ສະ ເໝີ ພາບ AM – GM , ລະບຸວ່າຕົວເລກເລກຄະນິດສາດຂອງບັນຊີຂອງຕົວເລກຕົວຈິງທີ່ບໍ່ລົບແມ່ນສູງກວ່າຫຼືເທົ່າກັບຄ່າເລຂາຄະນິດເລຂາຄະນິດດຽວກັນ; ແລະໃນຕໍ່ ໜ້າ, ທັງສອງວິທີແມ່ນເທົ່າທຽມກັນຖ້າວ່າແລະທຸກໆຕົວເລກໃນບັນຊີແມ່ນເທົ່າກັນ.
Norm (ຄະນິດສາດ): ໃນທາງຄະນິດສາດ, ບັນທັດ ຖານ ແມ່ນ ໜ້າ ທີ່ຈາກຊ່ອງ vector ທີ່ແທ້ຈິງຫຼືສັບຊ້ອນຈົນເຖິງຕົວເລກຕົວຈິງທີ່ບໍ່ມີຕົວຕົນທີ່ມີພຶດຕິ ກຳ ໃນບາງວິທີເຊັ່ນວ່າໄລຍະຫ່າງຈາກຕົ້ນ ກຳ ເນີດ: ມັນ ດຳ ເນີນໄປດ້ວຍຂະ ໜາດ, ປະຕິບັດຕາມຮູບແບບຂອງສາມຫຼ່ຽມສາມຫລ່ຽມ, ແລະແມ່ນສູນເທົ່ານັ້ນ ຕົ້ນກໍາເນີດ. ໂດຍສະເພາະ, ໄລຍະຫ່າງ Euclidean ຂອງ vector ຈາກຕົ້ນ ກຳ ເນີດແມ່ນບັນທັດຖານ, ເອີ້ນວ່າ Euclidean norm, ຫຼື 2-norm, ເຊິ່ງຍັງອາດຈະຖືກ ກຳ ນົດວ່າເປັນຮາກສີ່ຫລ່ຽມຂອງຜະລິດຕະພັນພາຍໃນຂອງ vector ດ້ວຍຕົວມັນເອງ.
ເລກຄະນິດສາດ: ໃນທິດສະດີ ຈຳ ນວນ, ເລກເລກເລກ ເປັນຕົວເລກ ສຳ ລັບການຄິດສະເລ່ຍຂອງຕົວເລກບວກຂອງມັນແມ່ນຕົວເລກ ໜຶ່ງ. ຍົກຕົວຢ່າງ, 6 ແມ່ນຕົວເລກເລກຄະນິດສາດເພາະວ່າສະເລ່ຍຂອງຕົວເລກຂອງມັນແມ່ນ
ເລກຄະດີຂອງການຄາດຕະ ກຳ: Arithmetic of a Murder ແມ່ນຮູບເງົາອາຊະຍາ ກຳ ໂຊວຽດປີ 1991 ທີ່ ກຳ ກັບໂດຍ Dmitry Svetozarov.
ເລກຄະນິດສາດຂອງແນວພັນ abelian: ໃນຄະນິດສາດ, ເລກຄະນິດສາດຂອງແນວພັນ abelian ແມ່ນການສຶກສາທິດສະດີເລກຂອງແນວພັນ abelian, ຫຼືຄອບຄົວຂອງແນວພັນ abelian. ມັນກັບຄືນໄປບ່ອນການສຶກສາຂອງ Pierre de Fermat ກ່ຽວກັບສິ່ງທີ່ຖືກຮັບຮູ້ໃນປັດຈຸບັນວ່າເປັນເສັ້ນໂຄ້ງ elliptic; ແລະໄດ້ກາຍເປັນພື້ນທີ່ທີ່ ສຳ ຄັນຂອງເລຂາຄະນິດກ່ຽວກັບເລກຄະນິດສາດທັງໃນແງ່ຂອງຜົນແລະການສົນທະນາ. ສ່ວນໃຫຍ່ຂອງສິ່ງເຫຼົ່ານີ້ສາມາດຖືກ ນຳ ມາໃຊ້ ສຳ ລັບແນວພັນ A abelian A ໃນໄລຍະພາກສະ ໜາມ K ; ຫຼືໂດຍທົ່ວໄປແລ້ວ.
ເລກຄະນິດສາດຂອງແນວພັນ abelian: ໃນຄະນິດສາດ, ເລກຄະນິດສາດຂອງແນວພັນ abelian ແມ່ນການສຶກສາທິດສະດີເລກຂອງແນວພັນ abelian, ຫຼືຄອບຄົວຂອງແນວພັນ abelian. ມັນກັບຄືນໄປບ່ອນການສຶກສາຂອງ Pierre de Fermat ກ່ຽວກັບສິ່ງທີ່ຖືກຮັບຮູ້ໃນປັດຈຸບັນວ່າເປັນເສັ້ນໂຄ້ງ elliptic; ແລະໄດ້ກາຍເປັນພື້ນທີ່ທີ່ ສຳ ຄັນຂອງເລຂາຄະນິດກ່ຽວກັບເລກຄະນິດສາດທັງໃນແງ່ຂອງຜົນແລະການສົນທະນາ. ສ່ວນໃຫຍ່ຂອງສິ່ງເຫຼົ່ານີ້ສາມາດຖືກ ນຳ ມາໃຊ້ ສຳ ລັບແນວພັນ A abelian A ໃນໄລຍະພາກສະ ໜາມ K ; ຫຼືໂດຍທົ່ວໄປແລ້ວ.
ເລກຄະນິດສາດຂອງແນວພັນ abelian: ໃນຄະນິດສາດ, ເລກຄະນິດສາດຂອງແນວພັນ abelian ແມ່ນການສຶກສາທິດສະດີເລກຂອງແນວພັນ abelian, ຫຼືຄອບຄົວຂອງແນວພັນ abelian. ມັນກັບຄືນໄປບ່ອນການສຶກສາຂອງ Pierre de Fermat ກ່ຽວກັບສິ່ງທີ່ຖືກຮັບຮູ້ໃນປັດຈຸບັນວ່າເປັນເສັ້ນໂຄ້ງ elliptic; ແລະໄດ້ກາຍເປັນພື້ນທີ່ທີ່ ສຳ ຄັນຂອງເລຂາຄະນິດກ່ຽວກັບເລກຄະນິດສາດທັງໃນແງ່ຂອງຜົນແລະການສົນທະນາ. ສ່ວນໃຫຍ່ຂອງສິ່ງເຫຼົ່ານີ້ສາມາດຖືກ ນຳ ມາໃຊ້ ສຳ ລັບແນວພັນ A abelian A ໃນໄລຍະພາກສະ ໜາມ K ; ຫຼືໂດຍທົ່ວໄປແລ້ວ.
ເລກຄະນິດສາດພາກສະ ໜາມ: ໃນຄະນິດສາດ, ເລກຄະນິດສາດພາກສະ ໜາມ ແມ່ນເລກຄະນິດສາດໃນພາກສະ ໜາມ ທີ່ ຈຳ ກັດກົງກັນຂ້າມກັບເລກຄະນິດສາດໃນສະ ໜາມ ທີ່ມີ ຈຳ ນວນອົງປະກອບທີ່ບໍ່ມີຂອບເຂດ, ຄືພາກສະ ໜາມ ຂອງຕົວເລກສົມເຫດສົມຜົນ.
ເລກຄະນິດສາດ: ໃນຂົງເຂດຄະນິດສາດຂອງທິດສະດີທີ່ ກຳ ນົດໄວ້, ເລກຄະນິດສາດ ອະທິບາຍກ່ຽວກັບການປະຕິບັດງານ 3 ຢ່າງທີ່ປົກກະຕິກ່ຽວກັບເລກຕາມ ລຳ ດັບ: ເພີ່ມ, ການຄູນແລະການອອກ ກຳ ລັງກາຍ. ແຕ່ລະອັນສາມາດຖືກ ກຳ ນົດດ້ວຍສອງວິທີທີ່ແຕກຕ່າງກັນ: ໂດຍການສ້າງຊຸດທີ່ຖືກຕ້ອງຕາມລະບຽບທີ່ຊັດເຈນເຊິ່ງເປັນຕົວແທນໃຫ້ແກ່ຜົນໄດ້ຮັບຂອງການປະຕິບັດງານຫຼືໂດຍການ ນຳ ໃຊ້ການເອີ້ນຄືນທີ່ບໍ່ໄດ້ຮັບການໂອນ. ແບບຟອມປົກກະຕິຂອງ Cantor ສະ ໜອງ ວິທີການມາດຕະຖານຂອງການຂຽນແບບພິທີການ. ນອກ ເໜືອ ໄປຈາກການປະຕິບັດງານຕາມປະເພນີ ທຳ ມະດາແລ້ວນີ້, ຍັງມີ ທຳ ນຽມ ທຳ ມະດາຂອງ ທຳ ມະຊາດແລະການ ດຳ ເນີນງານທີ່ທັນສະ ໄໝ.
ເລກຄະນິດສາດ: Arithmetic ແມ່ນສາຂາຂອງຄະນິດສາດເຊິ່ງປະກອບດ້ວຍການສຶກສາຕົວເລກ, ໂດຍສະເພາະກ່ຽວກັບຄຸນລັກສະນະຂອງການປະຕິບັດງານແບບດັ້ງເດີມຂອງພວກມັນ - ເພີ່ມ, ການຫັກລົບ, ການຄູນ, ການແບ່ງ, ການອອກ ກຳ ລັງກາຍແລະການສະກັດເອົາຮາກ. ຄະນິດສາດແມ່ນສ່ວນ ໜຶ່ງ ຂອງທິດສະດີ, ແລະທິດສະດີເລກແມ່ນຖືວ່າເປັນ ໜຶ່ງ ໃນການແບ່ງຂັ້ນເທິງຂອງຄະນິດສາດທີ່ທັນສະ ໄໝ, ພ້ອມດ້ວຍຄະນິດສາດ, ເລຂາຄະນິດແລະການວິເຄາະ. ຄຳ ສັບກ່ຽວກັບ ເລກຄະນິດສາດ ແລະ ເລກຄະນິດສາດ ສູງ ໄດ້ຖືກ ນຳ ໃຊ້ຈົນຮອດຕົ້ນສະຕະວັດທີ 20 ເປັນສັບຄ້າຍຄືກັນ ສຳ ລັບ ທິດສະດີເລກ , ແລະບາງຄັ້ງກໍ່ຍັງໃຊ້ເພື່ອອ້າງອີງເຖິງສ່ວນ ໜຶ່ງ ທີ່ກວ້າງຂວາງຂອງທິດສະດີເລກ.
ເລກຄະນິດສາດ: Arithmetic ແມ່ນສາຂາຂອງຄະນິດສາດເຊິ່ງປະກອບດ້ວຍການສຶກສາຕົວເລກ, ໂດຍສະເພາະກ່ຽວກັບຄຸນລັກສະນະຂອງການປະຕິບັດງານແບບດັ້ງເດີມຂອງພວກມັນ - ເພີ່ມ, ການຫັກລົບ, ການຄູນ, ການແບ່ງ, ການອອກ ກຳ ລັງກາຍແລະການສະກັດເອົາຮາກ. ຄະນິດສາດແມ່ນສ່ວນ ໜຶ່ງ ຂອງທິດສະດີ, ແລະທິດສະດີເລກແມ່ນຖືວ່າເປັນ ໜຶ່ງ ໃນການແບ່ງຂັ້ນເທິງຂອງຄະນິດສາດທີ່ທັນສະ ໄໝ, ພ້ອມດ້ວຍຄະນິດສາດ, ເລຂາຄະນິດແລະການວິເຄາະ. ຄຳ ສັບກ່ຽວກັບ ເລກຄະນິດສາດ ແລະ ເລກຄະນິດສາດ ສູງ ໄດ້ຖືກ ນຳ ໃຊ້ຈົນຮອດຕົ້ນສະຕະວັດທີ 20 ເປັນສັບຄ້າຍຄືກັນ ສຳ ລັບ ທິດສະດີເລກ , ແລະບາງຄັ້ງກໍ່ຍັງໃຊ້ເພື່ອອ້າງອີງເຖິງສ່ວນ ໜຶ່ງ ທີ່ກວ້າງຂວາງຂອງທິດສະດີເລກ.
ເລກຄະນິດສາດ: Arithmetic ແມ່ນສາຂາຂອງຄະນິດສາດເຊິ່ງປະກອບດ້ວຍການສຶກສາຕົວເລກ, ໂດຍສະເພາະກ່ຽວກັບຄຸນລັກສະນະຂອງການປະຕິບັດງານແບບດັ້ງເດີມຂອງພວກມັນ - ເພີ່ມ, ການຫັກລົບ, ການຄູນ, ການແບ່ງ, ການອອກ ກຳ ລັງກາຍແລະການສະກັດເອົາຮາກ. ຄະນິດສາດແມ່ນສ່ວນ ໜຶ່ງ ຂອງທິດສະດີ, ແລະທິດສະດີເລກແມ່ນຖືວ່າເປັນ ໜຶ່ງ ໃນການແບ່ງຂັ້ນເທິງຂອງຄະນິດສາດທີ່ທັນສະ ໄໝ, ພ້ອມດ້ວຍຄະນິດສາດ, ເລຂາຄະນິດແລະການວິເຄາະ. ຄຳ ສັບກ່ຽວກັບ ເລກຄະນິດສາດ ແລະ ເລກຄະນິດສາດ ສູງ ໄດ້ຖືກ ນຳ ໃຊ້ຈົນຮອດຕົ້ນສະຕະວັດທີ 20 ເປັນສັບຄ້າຍຄືກັນ ສຳ ລັບ ທິດສະດີເລກ , ແລະບາງຄັ້ງກໍ່ຍັງໃຊ້ເພື່ອອ້າງອີງເຖິງສ່ວນ ໜຶ່ງ ທີ່ກວ້າງຂວາງຂອງທິດສະດີເລກ.
ເລກຄະນິດສາດ: Arithmetic ແມ່ນສາຂາຂອງຄະນິດສາດເຊິ່ງປະກອບດ້ວຍການສຶກສາຕົວເລກ, ໂດຍສະເພາະກ່ຽວກັບຄຸນລັກສະນະຂອງການປະຕິບັດງານແບບດັ້ງເດີມຂອງພວກມັນ - ເພີ່ມ, ການຫັກລົບ, ການຄູນ, ການແບ່ງ, ການອອກ ກຳ ລັງກາຍແລະການສະກັດເອົາຮາກ. ຄະນິດສາດແມ່ນສ່ວນ ໜຶ່ງ ຂອງທິດສະດີ, ແລະທິດສະດີເລກແມ່ນຖືວ່າເປັນ ໜຶ່ງ ໃນການແບ່ງຂັ້ນເທິງຂອງຄະນິດສາດທີ່ທັນສະ ໄໝ, ພ້ອມດ້ວຍຄະນິດສາດ, ເລຂາຄະນິດແລະການວິເຄາະ. ຄຳ ສັບກ່ຽວກັບ ເລກຄະນິດສາດ ແລະ ເລກຄະນິດສາດ ສູງ ໄດ້ຖືກ ນຳ ໃຊ້ຈົນຮອດຕົ້ນສະຕະວັດທີ 20 ເປັນສັບຄ້າຍຄືກັນ ສຳ ລັບ ທິດສະດີເລກ , ແລະບາງຄັ້ງກໍ່ຍັງໃຊ້ເພື່ອອ້າງອີງເຖິງສ່ວນ ໜຶ່ງ ທີ່ກວ້າງຂວາງຂອງທິດສະດີເລກ.
ການໄຫຼວຽນແບບຄົບວົງຈອນ: ໃນການຂຽນໂປແກຼມຄອມພິວເຕີ້, ເລກເຕັມເກີນ ກຳ ລັງ ເກີດຂື້ນເມື່ອການ ດຳ ເນີນງານກ່ຽວກັບເລກຄະນິດສາດພະຍາຍາມສ້າງມູນຄ່າຕົວເລກທີ່ຢູ່ນອກຂອບເຂດທີ່ສາມາດ ນຳ ມາສະແດງດ້ວຍຕົວເລກທີ່ ກຳ ນົດໄວ້ - ບໍ່ວ່າຈະສູງກວ່າລະດັບສູງສຸດຫລືຕ່ ຳ ກ່ວາມູນຄ່າຕົວແທນຕ່ ຳ ສຸດ.
P-adic L-function: ໃນຄະນິດສາດ, ໜ້າ ທີ່ p -adic zeta , ຫຼືຫຼາຍກວ່ານັ້ນທົ່ວໄປແມ່ນ p -adic L -function , ແມ່ນ ໜ້າ ທີ່ຄ້າຍຄືກັນກັບ ໜ້າ ທີ່ຂອງ Riemann zeta, ຫຼື L -functions ທົ່ວໄປຫຼາຍ, ແຕ່ວ່າໂດເມນແລະເປົ້າ ໝາຍ ແມ່ນ p-adic . ຕົວຢ່າງ, ໂດເມນສາມາດເປັນຕົວ ເລກ p -adic integers Z p , p -group ທີ່ມີຊື່ສຽງ , ຫຼື p -adic ຄອບຄົວຂອງຕົວແທນ Galois, ແລະຮູບພາບອາດຈະແມ່ນ ຕົວເລກ p -adic Q p ຫຼືການປິດ algebraic ຂອງມັນ.
ຕົວເລກທີ່ ສຳ ຄັນ: ຕົວເລກທີ່ ສຳ ຄັນ ຂອງຕົວເລກໃນ ຕຳ ແໜ່ງ ຕຳ ແໜ່ງ ແມ່ນຕົວເລກໃນ ຈຳ ນວນທີ່ ໜ້າ ເຊື່ອຖືແລະ ຈຳ ເປັນແທ້ໆເພື່ອສະແດງ ຈຳ ນວນຂອງບາງສິ່ງບາງຢ່າງ. ຖ້າຕົວເລກທີ່ສະແດງຜົນຂອງການວັດແທກຂອງບາງສິ່ງບາງຢ່າງມີຕົວເລກຫຼາຍກ່ວາຕົວເລກທີ່ອະນຸຍາດໃນການແກ້ໄຂການວັດແທກ, ມີພຽງຕົວເລກທີ່ອະນຸຍາດໃຫ້ໂດຍການແກ້ໄຂການວັດແທກທີ່ເຊື່ອຖືໄດ້ດັ່ງນັ້ນພຽງແຕ່ເຫຼົ່ານີ້ສາມາດເປັນຕົວເລກທີ່ ສຳ ຄັນ. ຍົກຕົວຢ່າງ, ຖ້າການວັດແທກຄວາມຍາວໃຫ້ 114,8 ມມໃນຂະນະທີ່ໄລຍະຫ່າງນ້ອຍທີ່ສຸດລະຫວ່າງເຄື່ອງ ໝາຍ ເທິງໄມ້ທີ່ໃຊ້ໃນການວັດແທກແມ່ນ 1 ມມ, ຫຼັງຈາກນັ້ນສາມຕົວເລກ ທຳ ອິດມີຄວາມ ໜ້າ ເຊື່ອຖືເທົ່ານັ້ນຈຶ່ງສາມາດເປັນຕົວເລກທີ່ ສຳ ຄັນ. ໃນບັນດາຕົວເລກເຫຼົ່ານີ້, ມັນມີຄວາມບໍ່ແນ່ນອນໃນຕົວເລກສຸດທ້າຍແຕ່ມັນຍັງຖືວ່າເປັນຕົວເລກທີ່ ສຳ ຄັນເນື່ອງຈາກຕົວເລກທີ່ບໍ່ແນ່ນອນແຕ່ ໜ້າ ເຊື່ອຖືໄດ້ຖື ວ່າເປັນຕົວເລກທີ່ ສຳ ຄັນ. ຕົວຢ່າງອີກອັນ ໜຶ່ງ ແມ່ນການວັດແທກປະລິມານຂອງ 2.98 ລິດດ້ວຍຄວາມບໍ່ແນ່ນອນຂອງ± 0.05 L. ປະລິມານຕົວຈິງແມ່ນບາງບ່ອນລະຫວ່າງ 2,93 L ແລະ 3.03 L. ເຖິງແມ່ນວ່າຕົວເລກທັງສາມຕົວຈະບໍ່ແນ່ນອນແຕ່ ໜ້າ ເຊື່ອຖືເພາະສິ່ງເຫຼົ່ານີ້ສະແດງເຖິງປະລິມານຕົວຈິງກັບຄວາມບໍ່ແນ່ນອນທີ່ຍອມຮັບໄດ້ . ດັ່ງນັ້ນ, ເຫຼົ່ານີ້ແມ່ນຕົວເລກທີ່ ສຳ ຄັນ.
ຄວາມຄືບ ໜ້າ ເລກຄະນິດສາດ: ຄວາມຄືບ ໜ້າ ກ່ຽວກັບເລກຄະນິດສາດ (AP) ຫຼື ລຳ ດັບເລກຄະນິດສາດ ແມ່ນ ລຳ ດັບຂອງຕົວເລກດັ່ງກ່າວວ່າຄວາມແຕກຕ່າງລະຫວ່າງ ຄຳ ຕໍ່ເນື່ອງແມ່ນຄົງທີ່. ຍົກຕົວຢ່າງ, ລຳ ດັບ 5, 7, 9, 11, 13, 15,. .. ແມ່ນຄວາມຄືບ ໜ້າ ເລກຄະນິດສາດທີ່ມີຄວາມແຕກຕ່າງທົ່ວໄປຂອງ 2.
ເກມຄວາມຄືບຫນ້າກ່ຽວກັບເລກຄະນິດສາດ: ເກມ ຄວາມຄືບ ໜ້າ ກ່ຽວກັບເລກຄະນິດສາດ ແມ່ນເກມທີ່ຕັ້ງຢູ່ບ່ອນທີ່ຜູ້ຫຼິ້ນສອງຄົນເລືອກເອົາຕົວເລກ, ພະຍາຍາມທີ່ຈະຄອບຄອງຄວາມຄືບ ໜ້າ ກ່ຽວກັບເລກຄະນິດສາດທີ່ມີຂະ ໜາດ ໃດ ໜຶ່ງ.
ຄວາມຄືບ ໜ້າ ເລກຄະນິດສາດ: ຄວາມຄືບ ໜ້າ ກ່ຽວກັບເລກຄະນິດສາດ (AP) ຫຼື ລຳ ດັບເລກຄະນິດສາດ ແມ່ນ ລຳ ດັບຂອງຕົວເລກດັ່ງກ່າວວ່າຄວາມແຕກຕ່າງລະຫວ່າງ ຄຳ ຕໍ່ເນື່ອງແມ່ນຄົງທີ່. ຍົກຕົວຢ່າງ, ລຳ ດັບ 5, 7, 9, 11, 13, 15,. .. ແມ່ນຄວາມຄືບ ໜ້າ ເລກຄະນິດສາດທີ່ມີຄວາມແຕກຕ່າງທົ່ວໄປຂອງ 2.
ແຫວນ (ຄະນິດສາດ): ໃນຄະນິດສາດ, ແຫວນ ແມ່ນໂຄງສ້າງກ່ຽວກັບພຶດຊະຄະນິດທີ່ເຮັດໃຫ້ຂະ ແໜງ ວິທະຍາສາດທົ່ວໄປ: ຕົວເລກທະວີຄູນບໍ່ ຈຳ ເປັນຕ້ອງມີຕົວປ່ຽນແລະຕົວຄູນແບບທະວີຄູນບໍ່ ຈຳ ເປັນຕ້ອງມີ. ໃນຄໍາສັບຕ່າງໆອື່ນໆ, ແຫວນ ແມ່ນຊຸດທີ່ຕິດຕັ້ງກັບສອງປະຕິບັດການຄູ່ສອງຄຸນລັກສະນະທີ່ສົມບູນແບບຄ້າຍຄືກັນກັບສິ່ງທີ່ເພີ່ມເຕີມແລະຄູນເລກເຕັມ. ອົງປະກອບຂອງວົງແຫວນອາດຈະເປັນຕົວເລກເຊັ່ນເລກເຕັມຫລືຕົວເລກທີ່ຊັບຊ້ອນ, ແຕ່ມັນຍັງອາດຈະແມ່ນວັດຖຸທີ່ບໍ່ແມ່ນຕົວເລກເຊັ່ນ: polynomials, matrices ຮຽບຮ້ອຍ, ໜ້າ ທີ່ແລະຊຸດພະລັງງານ.
ລຳ ດັບຊັ້ນເລກຄະນິດສາດ: ໃນຄວາມ ໝາຍ ທາງຄະນິດສາດ, ລຳ ດັບຊັ້ນຄະນິດສາດ , ລຳ ດັບຊັ້ນ ເລກຄະນິດສາດ ຫຼື ລຳ ດັບຊັ້ນສູງ Kleene – Mostowski ແມ່ນ ກຳ ນົດບາງຊຸດໂດຍອີງໃສ່ຄວາມສັບສົນຂອງສູດທີ່ ກຳ ນົດພວກມັນ. ຊຸດໃດກໍ່ຕາມທີ່ໄດ້ຮັບການຈັດປະເພດແມ່ນຖືກເອີ້ນວ່າ ເລກຄະນິດສາດ .
ອັດຕາຜົນຕອບແທນ: ໃນດ້ານການເງິນ, ການ ກັບມາ ແມ່ນ ກຳ ໄລໃນການລົງທືນ. ມັນປະກອບມີການປ່ຽນແປງໃດໆກ່ຽວກັບມູນຄ່າການລົງທືນ, ແລະ / ຫຼືກະແສເງິນສົດທີ່ນັກລົງທຶນໄດ້ຮັບຈາກການລົງທືນນັ້ນ, ເຊັ່ນ: ການຈ່າຍດອກເບ້ຍ, ໃບບິນ, ເງິນປັນຜົນ, ເງິນປັນຜົນຫລືການຈ່າຍເງິນຈາກຜະລິດຕະພັນອະນຸພັນຫລືໂຄງສ້າງ. ມັນອາດຈະຖືກວັດແທກທັງໃນເງື່ອນໄຂຢ່າງແທ້ຈິງຫລືເປັນເປີເຊັນຂອງ ຈຳ ນວນເງິນທີ່ລົງທືນ. ສຸດທ້າຍກໍ່ຖືກເອີ້ນວ່າໄລຍະເວລາຖືຄອງ.
ການປ່ຽນແປງເລກຄະນິດສາດ: ໃນການຂຽນໂປແກຼມຄອມພິວເຕີ້, ການ ປ່ຽນເລກຄະນິດສາດ ແມ່ນຜູ້ປະຕິບັດການປ່ຽນແປງ, ບາງຄັ້ງກໍ່ເອີ້ນວ່າການ ປ່ຽນແປງທີ່ເຊັນ . ສອງປະເພດພື້ນຖານແມ່ນການ ເລື່ອນຊ້າຍດ້ານເລກເລກ ແລະການ ເລື່ອນຂວາດ້ານເລກເລກ . ສຳ ລັບຕົວເລກຖານສອງມັນແມ່ນການ ດຳ ເນີນງານທີ່ມີຄວາມ ໝາຍ ເລັກນ້ອຍທີ່ປ່ຽນສ່ວນທັງ ໝົດ ຂອງ ລຳ ດັບຂອງມັນ; ທຸກໆບິດໃນລະຄອນພຽງແຕ່ຍ້າຍ ຈຳ ນວນ ຕຳ ແໜ່ງ ນ້ອຍໆ, ແລະ ຕຳ ແໜ່ງ bit-vacant ທີ່ເຕັມໄປດ້ວຍ. ແທນທີ່ຈະເຕັມໄປດ້ວຍ 0s ທັງ ໝົດ, ຄືກັບການປ່ຽນທິດທາງທີ່ສົມເຫດສົມຜົນ, ເມື່ອປ່ຽນໄປທາງຂວາ, ສ່ວນທາງຊ້າຍແມ່ນຖືກປ່ຽນແທນ ຕື່ມທຸກ ຕຳ ແໜ່ງ ທີ່ວ່າງ.
ແຫວນເລກຄະນິດສາດ: ໃນພຶດຊະຄະນິດ, ວົງແຫວນການປ່ຽນແປງ R ຖືກກ່າວເຖິງເປັນ ເລກຄະນິດສາດ ຖ້າມີເງື່ອນໄຂທຽບເທົ່າດັ່ງຕໍ່ໄປນີ້: ທ້ອງຖິ່ນ ຂອງ R ຢູ່ ແມ່ນແຫວນທີ່ບໍ່ມີສາຍ ສຳ ລັບທຸກໆຈຸດສູງສຸດທີ່ ເໝາະ ສົມ ຂອງ R. ສຳ ລັບອຸດົມການທັງ ໝົດ , ແລະ , ສຳ ລັບອຸດົມການທັງ ໝົດ , ແລະ ,